Содержание
- 2. Длина кривой Если функции f1(t), f2(t), f3(t) непрерывно дифференцируемы, то кривая L называется гладкой кривой (кривая
- 3. Длина кривой Теорема. Гладкая кривая спрямляема и ее длина удовлетворяет неравенствам где
- 4. Длина кривой Рассмотрим гладкую кривую Пусть Теорема. Для любой гладкой кривой
- 5. Длина кривой Доказательство. Пусть t>t0, тогда по теореме об аддитивности длины Согласно предыдущей теореме для отрезка
- 6. Длина кривой Если t Согласно предыдущей теореме для отрезка [t; t0]
- 7. Длина кривой Отсюда следует, что
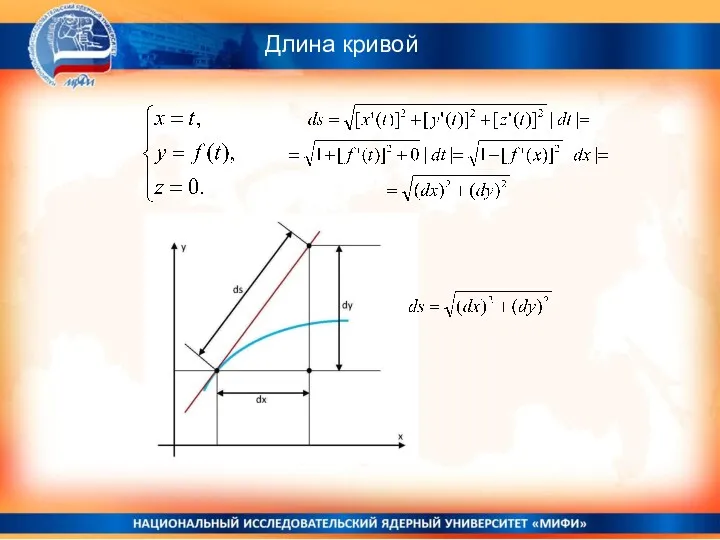
- 8. Длина кривой Элемент длины дуги Определение. Модуль дифференциала длины дуги называется элементом длины дуги. (теорема Пифагора
- 9. Длина кривой
- 10. Касательная к кривой
- 11. Касательная к кривой Предельное значение этого вектора при t→t0 (в том случае, когда оно отлично от
- 12. Касательная к кривой Особые и регулярные точки кривой В регулярной точке кривая всегда имеет касательную.
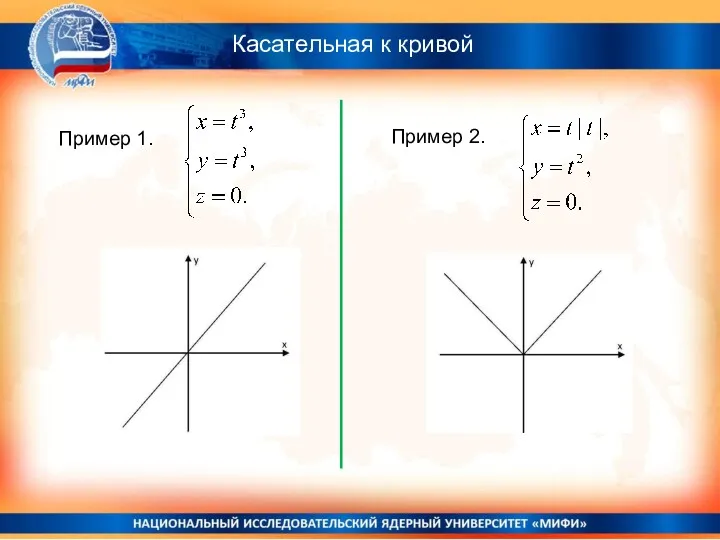
- 13. Касательная к кривой Пример 1. Пример 2.
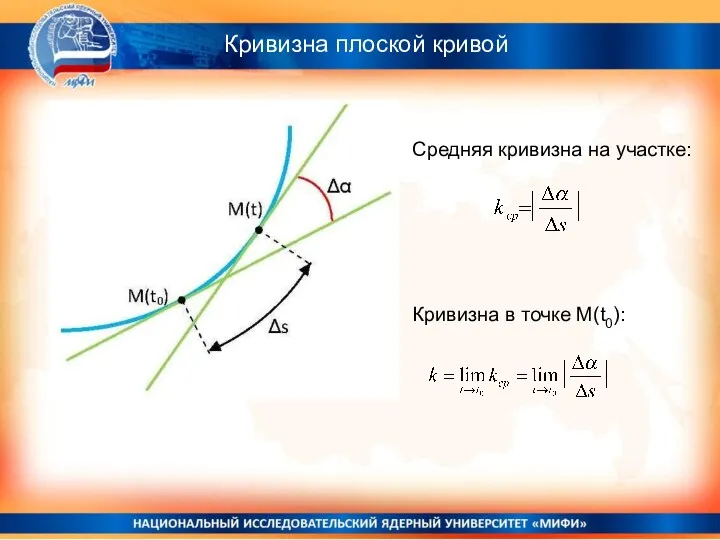
- 14. Кривизна плоской кривой Средняя кривизна на участке: Кривизна в точке M(t0):
- 15. Кривизна плоской кривой Теорема. Пусть на плоскости задана гладкая регулярная кривая Тогда ее кривизна в каждой
- 16. Кривизна плоской кривой Доказательство. Так как кривая регулярна, то величина Пусть для определенности Касательный вектор к
- 17. Кривизна плоской кривой По определению кривизны
- 18. Кривизна плоской кривой то Так как
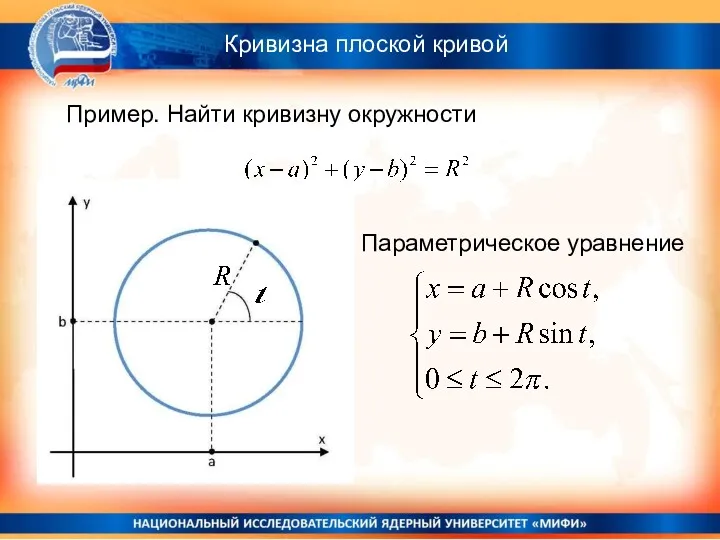
- 19. Кривизна плоской кривой Пример. Найти кривизну окружности Параметрическое уравнение
- 20. Кривизна плоской кривой
- 21. Кривизна плоской кривой Часто представляется удобным приближенно заменять кривую вблизи рассматриваемой точки – окружностью, имеющую ту
- 22. Кривизна плоской кривой Если кривая задана в параметрической форме то координаты центра кривизны кривой в точке
- 23. Кривизна плоской кривой Если кривая задана как график явной функции то параметрическое уравнение этой кривой имеет
- 24. Эволюта плоской кривой Геометрическое множество центров кривизны данной кривой называется ее эволютой. Сама кривая по отношению
- 25. Эволюта плоской кривой Из полученных уравнений Исключаем y и получаем уравнение эволюты
- 26. Метод итераций (последовательных приближений) Замечание.
- 27. Метод итераций Принцип сжимающих отображений Пусть выполнены следующие условия Тогда на отрезке [a,b] существует и притом
- 28. Метод итераций Доказательство. В силу условия (1) последовательность итераций определена. Покажем, что она фундаментальна. Лемма. При
- 29. Метод итераций Оценим, теперь, величину Итак, мы имеем два неравенства Из которых следует, что при m≥n
- 30. Метод итераций
- 31. Метод итераций
- 32. Метод итераций Единственность решения.
- 33. Иоганн Кеплер 27.12.1571 – 15.11.1630 Немецкий математик, астроном и оптик, первооткрыватель законов движения планет Солнечной системы.
- 34. Иоганн Кеплер В 1612 году Кеплер переезжает в Линц, где прожил 14 лет. За ним сохранена
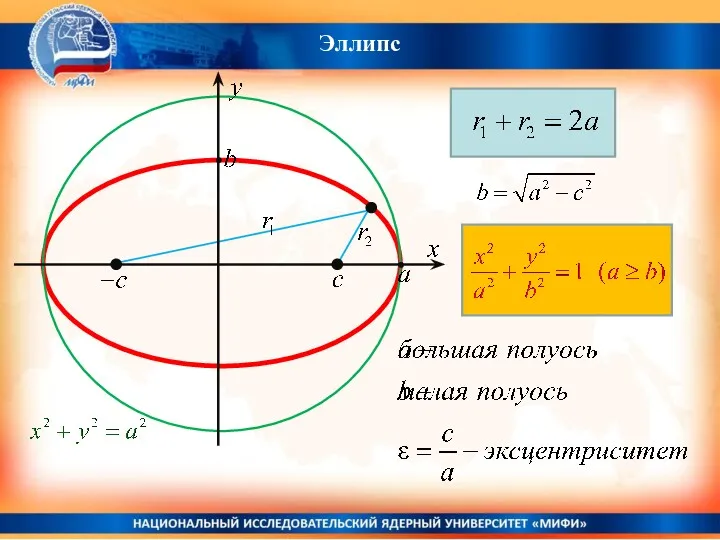
- 35. Эллипс
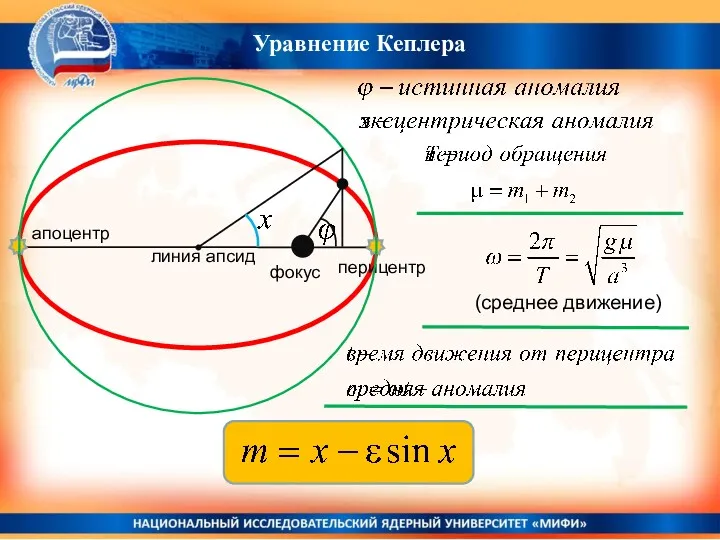
- 36. Уравнение Кеплера перицентр фокус апоцентр линия апсид (среднее движение)
- 37. Метод итераций (пример) Уравнение Кеплера Таким образом, итерации сходятся к единственному решению этого уравнения.
- 38. Метод итераций (пример) Оценка погрешности: 1619 Ответ:
- 40. Скачать презентацию




![Длина кривой Если t Согласно предыдущей теореме для отрезка [t; t0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/185916/slide-5.jpg)


























 Геометрические основы компьютерной графики
Геометрические основы компьютерной графики Сложение и вычитание десятичных дробей. 5 класс
Сложение и вычитание десятичных дробей. 5 класс Introduction to Statistics. Week 1 (1)
Introduction to Statistics. Week 1 (1) Математика. Приклади. Диск
Математика. Приклади. Диск П’єр де Ферма
П’єр де Ферма КАЖДЫЙ ДЕНЬ ЖИЗНИ ПРИБАВЛЯЕТ ЧАСТИЧКУ МУДРОСТИ
КАЖДЫЙ ДЕНЬ ЖИЗНИ ПРИБАВЛЯЕТ ЧАСТИЧКУ МУДРОСТИ Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Задачи на построение
Задачи на построение Сложение и вычитание одночленов
Сложение и вычитание одночленов Шар, сфера урок математики, 6 класс
Шар, сфера урок математики, 6 класс Прямая и обратная пропорциональность. Решение задач
Прямая и обратная пропорциональность. Решение задач Графики тригонометрических функций
Графики тригонометрических функций Модуль числа
Модуль числа Подобие фигур
Подобие фигур Координатная прямая. Урок 14
Координатная прямая. Урок 14 Окружность, круг и их элементы
Окружность, круг и их элементы Многоугольник. Прямоугольник. Площадь многоугольника
Многоугольник. Прямоугольник. Площадь многоугольника Теорема Пифагора. Урок №2. Решение задач
Теорема Пифагора. Урок №2. Решение задач Интересные факты из жизни Пифагора Самосского
Интересные факты из жизни Пифагора Самосского Старинные измерения величин
Старинные измерения величин Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Параллелепипед
Параллелепипед Рабочая учебная программа развития логического мышления у детей 6 – 7 лет на основе занимательной математики Логика
Рабочая учебная программа развития логического мышления у детей 6 – 7 лет на основе занимательной математики Логика конспект итогового открытого занятия по ФЭМП в старшей группе Путешествие в страну математики.
конспект итогового открытого занятия по ФЭМП в старшей группе Путешествие в страну математики. Уравнения прямой и окружности
Уравнения прямой и окружности Понятие об измерении
Понятие об измерении Решение неполных квадратных уравнений
Решение неполных квадратных уравнений Трудные случаи таблицы умножения и деления
Трудные случаи таблицы умножения и деления