Содержание
- 2. Про соревнования 3 мая 2013 Соревнования будут проходить в пятницу 3 мая, с 14-00, в 305-307
- 3. План лекции Перестановки и инверсии Инверсии Связь со сложностью сортировки Алгоритм восстановления перестановки по таблице инверсий
- 4. Перестановки Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке Для объектов
- 5. Перестановки Для множества из N элементов можно построить N! различных перестановок Первую позицию можно занять N
- 6. Пусть даны множество из N элементов 1,2, 3,..., N и его перестановка Пара называется инверсией (инверсионной
- 7. Перестановка 4, 1, 3, 2 имеет четыре инверсии (4,1), (3,2), (4,3) и (4,2) Почему? Инверсии --
- 8. Таблица инверсий Таблицей инверсий перестановки а1, а2, ..., aN называется последовательность чисел b1, b2, …, bN,
- 9. Свойства таблиц инверсий Для элементов таблицы инверсий справедливы неравенства bN = 0 0 0 Таблица инверсий
- 10. Построение перестановки по таблице инверсий На каждом шаге вставляем следующий по величине элемент с учетом того,
- 11. Построение перестановки по таблице инверсий справа налево Вход N > 0 - количество элементов перестановки b1,
- 12. Создается заготовка пустой перестановки длины N На каждом шаге для каждого элемента перестановки, начиная с 1,
- 13. Построение перестановки по таблице инверсий слева направо Вход N > 0 - количество элементов перестановки b1,
- 14. Инверсионный метод поиска всех перестановок Таблицы инверсий взаимно однозначно соответствуют перестановкам Почему? Перебор ТИ сводится к
- 15. Инверсионный метод поиска всех перестановок Рассмотрим таблицу инверсий как N-значное число в «системе счисления», где количество
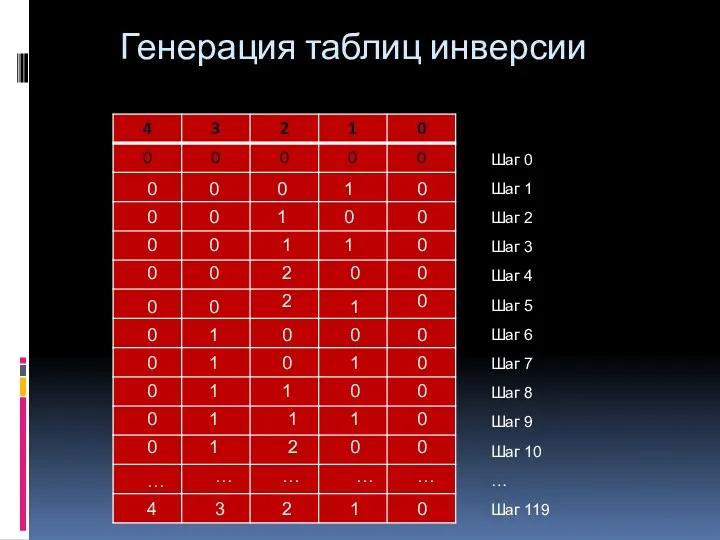
- 16. Генерация таблиц инверсии 0 0 0 0 0 0 0 0 0 1 1 1 …
- 17. Нахождение следующей таблицы инверсий B = b1, b2, ..., bN – ТИ i = N не_всё
- 18. Поиск следующей по алфавиту перестановки (алг. Дейкстры) П. b = b1, b2, …, bN предшествует п.
- 19. Алгоритм Дейкстры От заданной перестановки перейдем к следующей за ней в алфавитном порядке и т.д., пока
- 20. Генерация следующей по алфавиту перестановки Вход П = a1, a2, …, a[N-1], aN – перестановка N
- 21. Для перестановки 1 4 6 2 9 5 8 7 3 Найти следующую по алфавиту. 1
- 22. Рекурсивный метод поиска всех перестановок
- 23. Пример рекурсивного перебора для M= {1,2,3,4} Реr(M) Р ({2,3,4}) Р ({1,3,4}) Р ({1,2,4}) Р ({1,2,3}) Р
- 24. Реализация на языке Си typedef char string[256]; void permut(string start, string rest) { int lenr =
- 25. Реализация на языке Си #include typedef char mystring_t[256]; void permut(mystring_t start, mystring_t rest) { int lenr
- 26. Генерация всех перестановок методом Кнута Идея Рекурсивная генерация начиная с пустой перестановки методом расширения базового множества
- 27. Генерация перестановок методом Кнута – способ 1 Пусть дана перестановка длины N Допишем в конец перестановки
- 28. Генерация перестановок методом Кнута – способ 2 Пусть дана перестановка длины N: a1 a2 … aN
- 30. Скачать презентацию





















![Реализация на языке Си typedef char string[256]; void permut(string start,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/274108/slide-23.jpg)
![Реализация на языке Си #include typedef char mystring_t[256]; void permut(mystring_t](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/274108/slide-24.jpg)



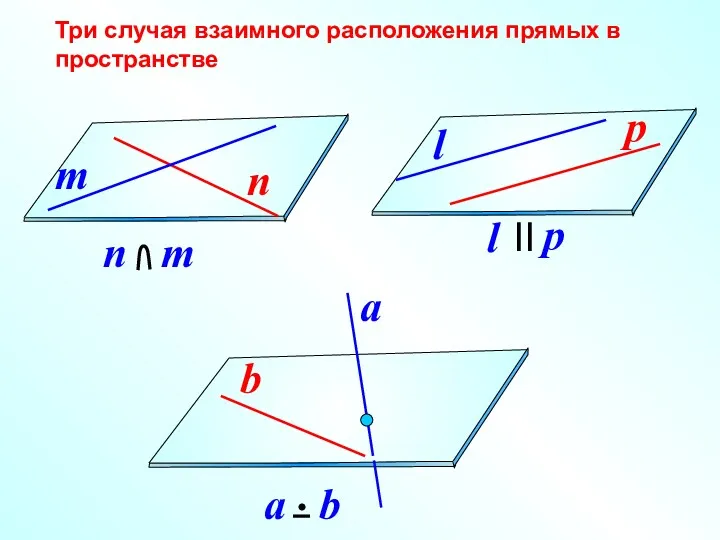 Параллельность прямой и плоскости
Параллельность прямой и плоскости Фрагмент уроку математики. Каліграфічна хвилинка
Фрагмент уроку математики. Каліграфічна хвилинка Волшебство чисел. Закон девятки
Волшебство чисел. Закон девятки Математика вокруг нас
Математика вокруг нас Наименьшее общее кратное
Наименьшее общее кратное Старинные русские меры длины и веса
Старинные русские меры длины и веса Дидактические игры на уроках математики
Дидактические игры на уроках математики Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Математика в жизни человека
Математика в жизни человека Комплексные числа
Комплексные числа Принцип Дирихле
Принцип Дирихле Дискриминант квадратных уравнений
Дискриминант квадратных уравнений Приемы устного счета
Приемы устного счета Неравенство треугольника
Неравенство треугольника Сложение и вычитание смешанных чисел (урок математики в 6 классе)
Сложение и вычитание смешанных чисел (урок математики в 6 классе) Задачи на готовых чертежах Смежные и вертикальные углы
Задачи на готовых чертежах Смежные и вертикальные углы Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Правильные многоугольники
Правильные многоугольники Умножение и деление на однозначное число
Умножение и деление на однозначное число Урок математики. Многозначные числа и действия с ними.
Урок математики. Многозначные числа и действия с ними. Веселый счет
Веселый счет Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Отрезок. Длина отрезка
Отрезок. Длина отрезка Противоположные числа
Противоположные числа Метр — одиниця довжини
Метр — одиниця довжини Решение простейших тригонометрических уравнений - 2
Решение простейших тригонометрических уравнений - 2 Функция арифметического квадратного корня, её свойства и график
Функция арифметического квадратного корня, её свойства и график Свойства квадратного корня
Свойства квадратного корня