Содержание
- 2. Термин “пирамида” заимствован из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как
- 3. На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса
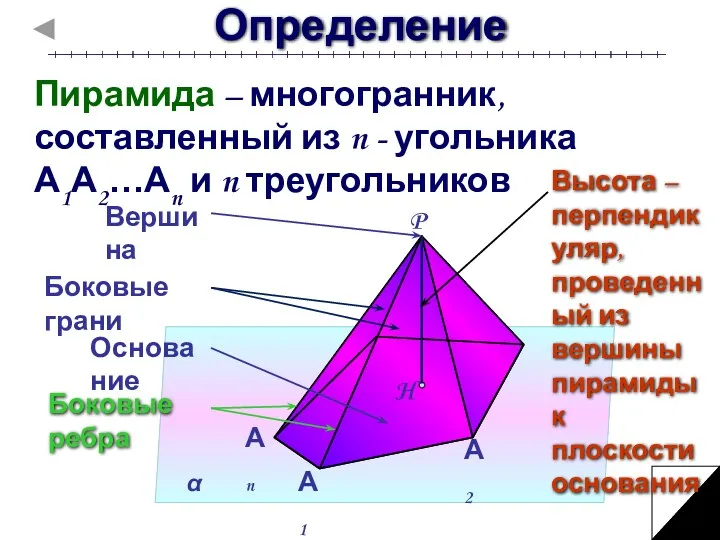
- 4. Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр,
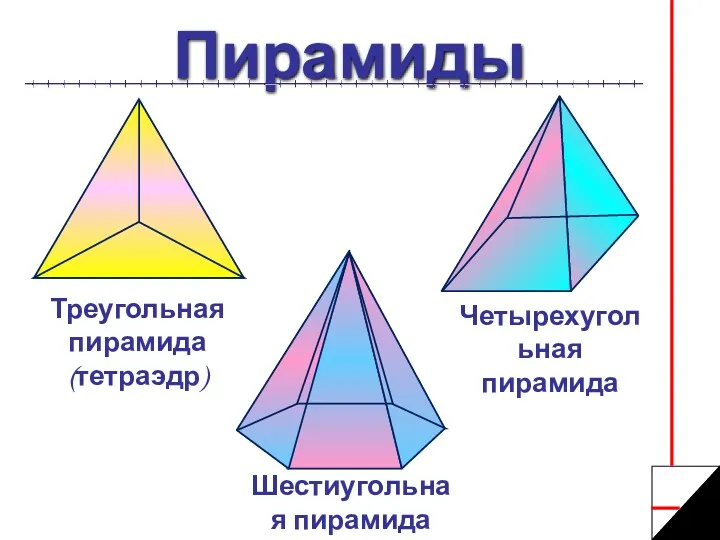
- 5. Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида
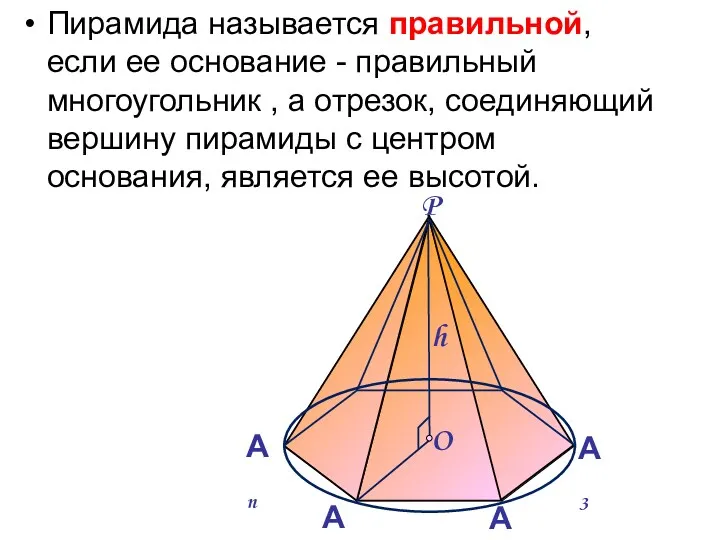
- 6. Пирамида называется правильной, если ее основание - правильный многоугольник , а отрезок, соединяющий вершину пирамиды с
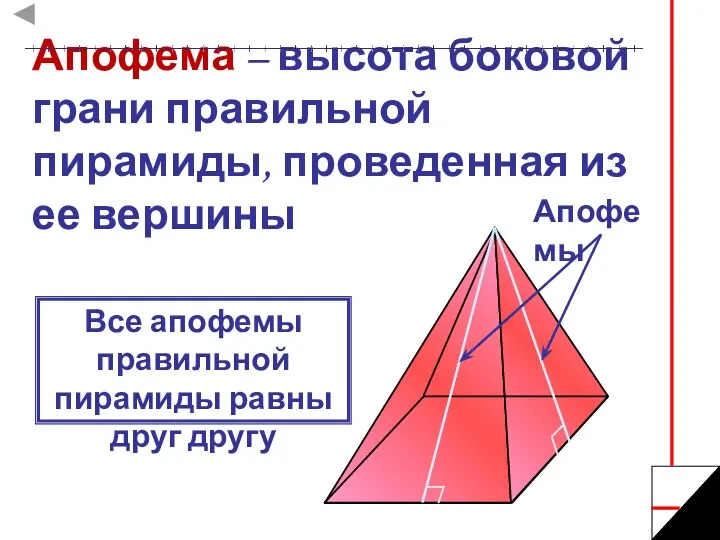
- 7. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Апофемы Все апофемы правильной пирамиды
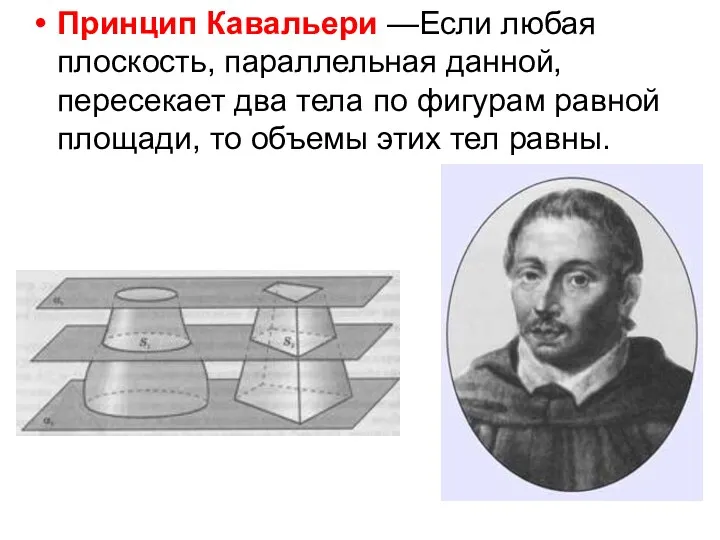
- 8. Принцип Кавальери —Если любая плоскость, параллельная данной, пересекает два тела по фигурам равной площади, то объемы
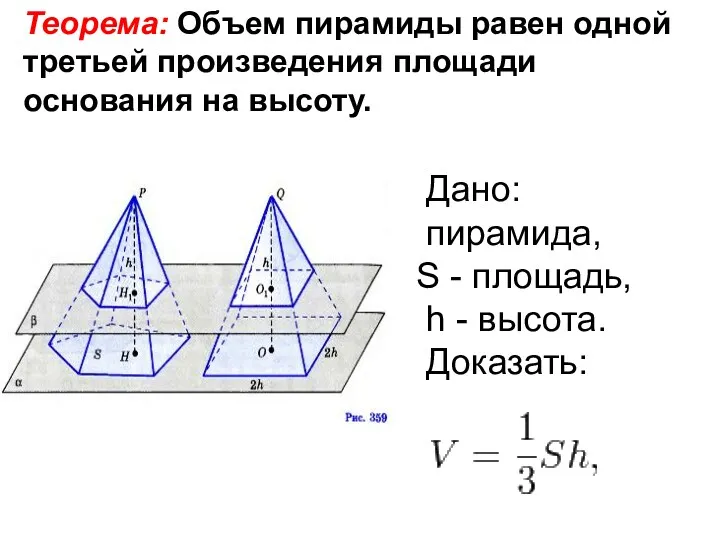
- 9. Теорема: Объем пирамиды равен одной третьей произведения площади основания на высоту. Дано: пирамида, S - площадь,
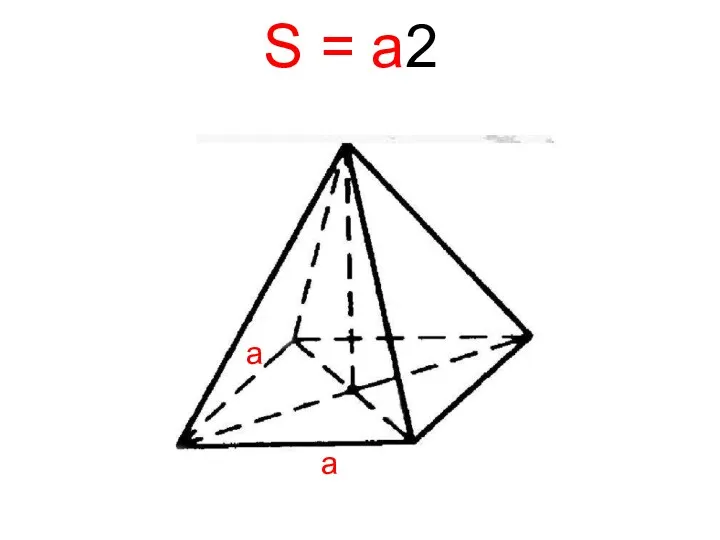
- 10. S = a2 а а
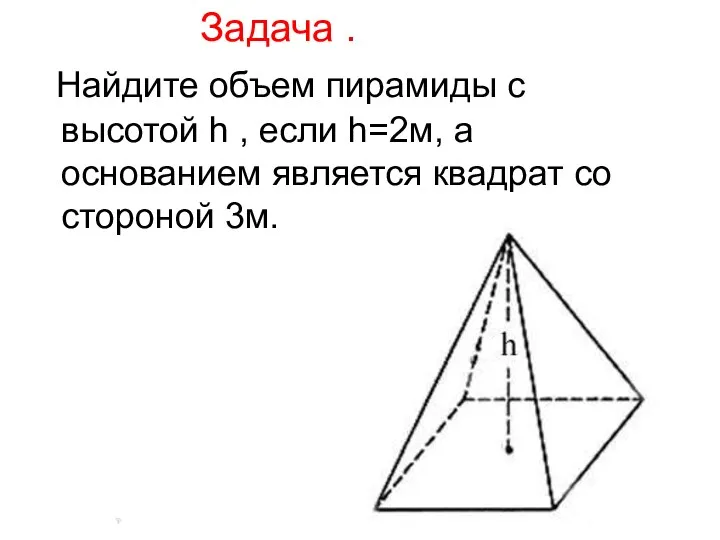
- 11. Задача . Найдите объем пирамиды с высотой h , если h=2м, а основанием является квадрат со
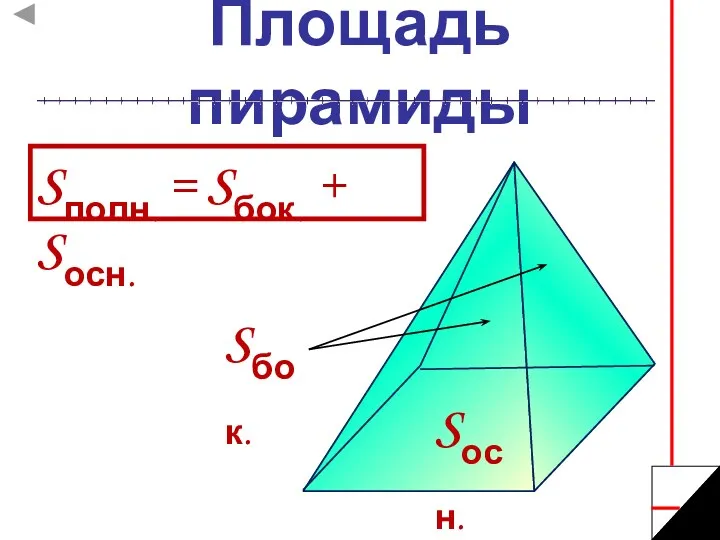
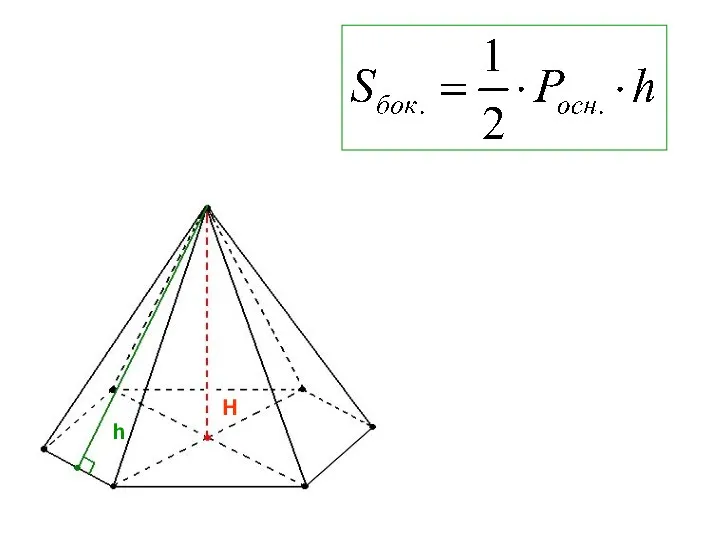
- 12. Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
- 13. h H
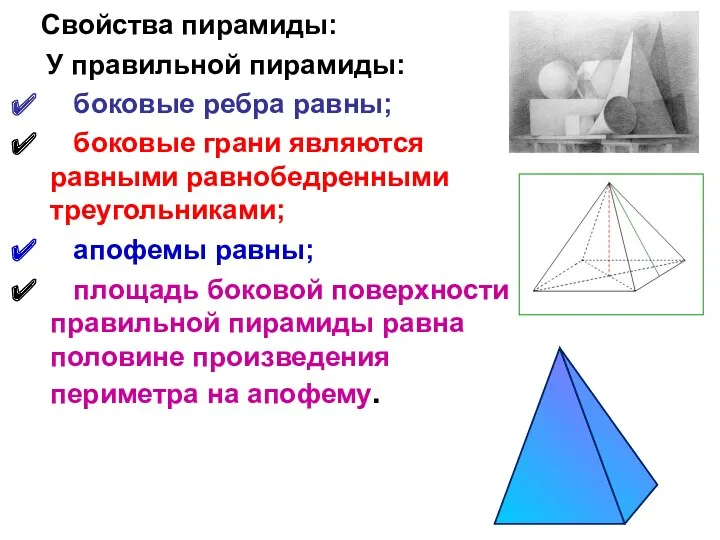
- 14. Свойства пирамиды: У правильной пирамиды: боковые ребра равны; боковые грани являются равными равнобедренными треугольниками; апофемы равны;
- 17. Скачать презентацию



 Пирамида
Пирамида Деление на десятичную дробь
Деление на десятичную дробь Проценты
Проценты Игра-тренажер 1 класс Состав чисел 14-18 , примеры
Игра-тренажер 1 класс Состав чисел 14-18 , примеры Правильные и неправильные дроби
Правильные и неправильные дроби Единицы длины – дециметр
Единицы длины – дециметр Приведение подобных слагаемых
Приведение подобных слагаемых Представление многозначных чисел в виде суммы разрядных слагаемых
Представление многозначных чисел в виде суммы разрядных слагаемых Правильные многогранники. Решение задач
Правильные многогранники. Решение задач ДУ второго порядка, допускающие понижение степени
ДУ второго порядка, допускающие понижение степени Решение уравнения Cos x=a
Решение уравнения Cos x=a Системы счисления. Арифметические действия над систематическими числами
Системы счисления. Арифметические действия над систематическими числами Презентация. Математическая сказка Колобок 1 класс.
Презентация. Математическая сказка Колобок 1 класс. Арифметическая прогрессия
Арифметическая прогрессия Презентация Прощай, 1 класс
Презентация Прощай, 1 класс Метод интервалов
Метод интервалов Числа от 1 до 20. Десятичный состав чисел второго десятка.
Числа от 1 до 20. Десятичный состав чисел второго десятка. Математика 4 класс СКОРОСТЬ
Математика 4 класс СКОРОСТЬ Методика изучения элементов геометрии
Методика изучения элементов геометрии Семейство четырехугольников
Семейство четырехугольников Деление многозначных чисел
Деление многозначных чисел Математический диктант
Математический диктант Теорема Пифагор
Теорема Пифагор Задача по финансовой математике
Задача по финансовой математике Solution methods for bilevel optimization
Solution methods for bilevel optimization Вписані і центральні кути
Вписані і центральні кути Зеркальное отражение предметов
Зеркальное отражение предметов Интегрированный урок математики и окружающего мира в 3 классе Письменное сложение и вычитание трёхзначных чисел( презентация )
Интегрированный урок математики и окружающего мира в 3 классе Письменное сложение и вычитание трёхзначных чисел( презентация )