Понятие функции, способы её задания, график функции. Преобразование графиков презентация

Числовая функция
Определение. Числовой функцией с областью определения D называется соответствие при котором каждому числу x из множества D сопоставляется по некоторому правилу число y, зависящее от x.
x – аргумент функции (независимая переменная)
Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x)

Область определения функции f обозначают D(f).
Множество, состоящее из всех чисел f(x), таких, что х принадлежит области определения функции f, называют областью значений функции f и обозначают E(f).

Объединением множеств А и В называется множество, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В.
Объединение множеств А и В обозначается так:

Функции вида f(x)=p(x), где p(x) – многочлен, называют целыми рациональными функциями, а функции вида
где p(x) и q(x) – многочлены, называют дробно-рациональными функциями.

График функции
Графиком функции f называют множество всех точек (х, у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.
0
x
y
y=f(x)

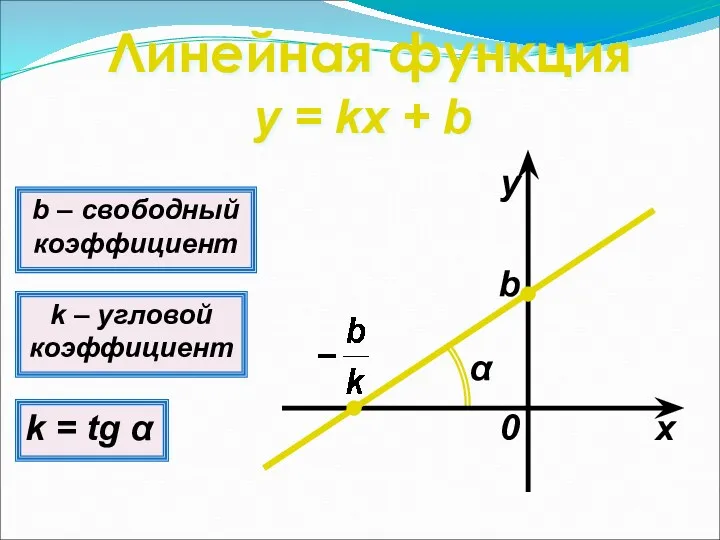
Линейная функция
y = kx + b
k – угловой
коэффициент
k = tg α
b – свободный
коэффициент
b
x
y
α
0

Свойства линейной функции
1о D(y) = (−∞; +∞); E(y) = (−∞; +∞).
2о Если b = 0, то функция нечетная.
Если b ≠ 0, то функция ни четная, ни нечетная.
3о Если х = 0, то у = b, если у = 0, то х = − .
4о Если k > 0, то функция возрастает при х (−∞; +∞).
Если k < 0, то функция убывает при х (−∞; +∞).
y = kx + b

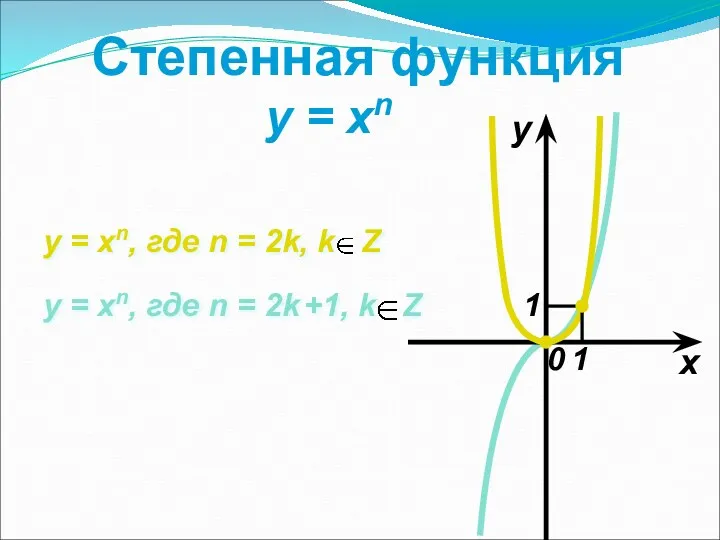
Степенная функция
y = xn
x
y
0
y = xn, где n = 2k, k Z
y = xn, где n = 2k +1, k Z
1
1

Свойства степенной функции
y = xn
Если n = 2k, где k  Z
1о D(y)=(−∞; +∞).
2о E(y)=[0 ; +∞).
3о Функция четная.
4о Если х = 0, то у = 0.
5о Функция возрастает
при х[0 ; +∞);
убывает при х(−∞; 0].
Если n = 2k +1, где k  Z
1о D(y)=(−∞; +∞).
2о E(y)=(−∞; +∞).
3о Функция нечетная.
4о Если х = 0, то у = 0.
5о Функция возрастает
при х(−∞; +∞).

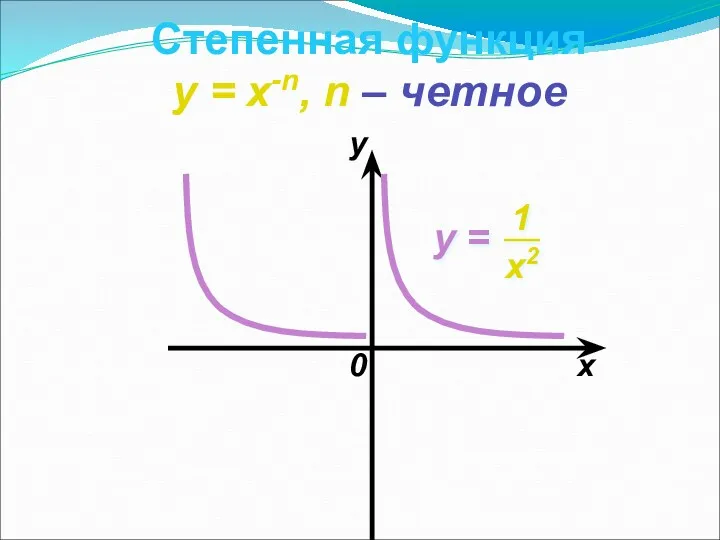
Степенная функция
y = x-n, n – четное
0
x
y

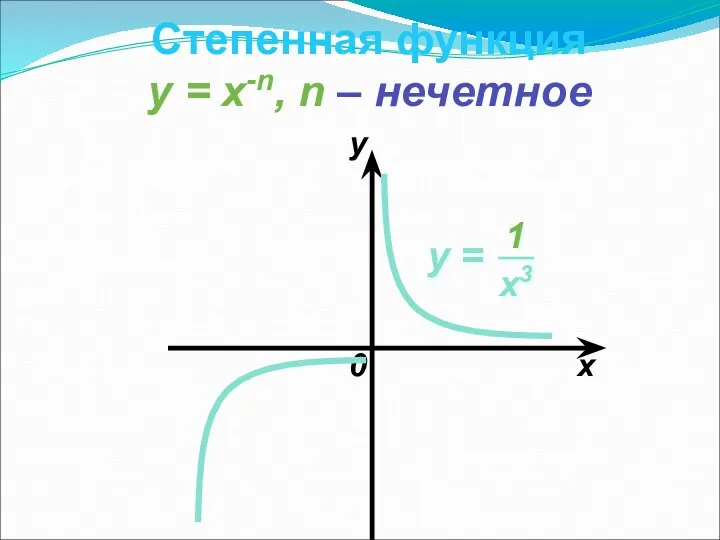
0
x
y
Степенная функция
y = x-n, n – нечетное

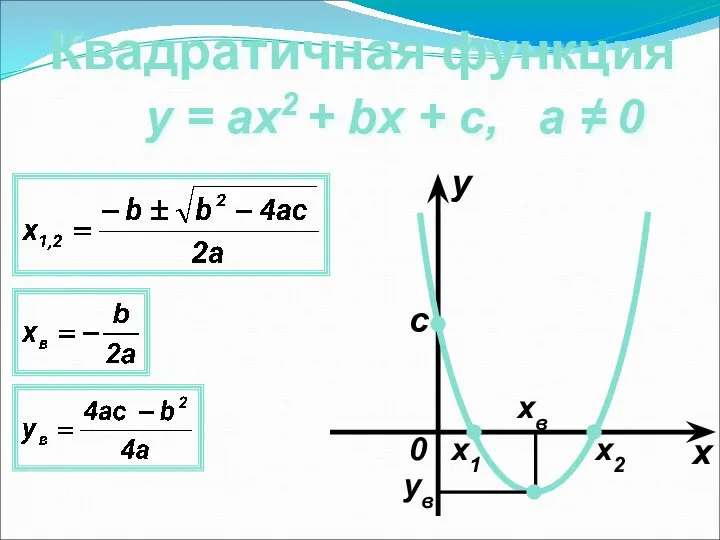
Квадратичная функция
y = ax2 + bx + c, а ≠ 0
x
y
0
c
x1
x2
xв
ув

Свойства квадратичной функции
1о D(y) = (−∞; +∞).
2о Если a > 0, то E(y) = [ув ; +∞);
Если a < 0, то E(y) = (−∞; ув ].
3о Если b = 0, то функция четная.
Если b ≠ 0, то функция ни четная, ни нечетная.
4о Если х = 0, то у = c, если у = 0, то х1,2 =
5о Если a > 0, то функция возрастает при х[xв ; +∞);
функция убывает при х(−∞; хв ].
Если a < 0, то функция возрастает при х(−∞; хв ];
функция убывает при х[xв ; +∞).
y = ax2 + bx + c, а ≠ 0

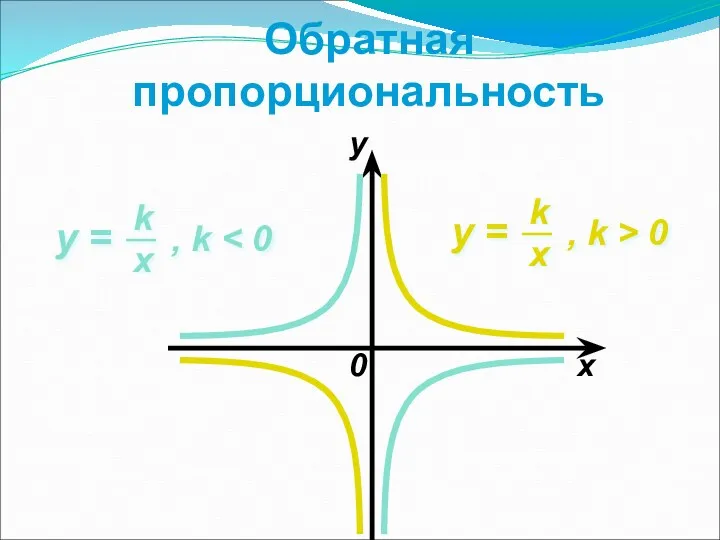
Обратная
пропорциональность
0
x
y

Свойства обратной пропорциональности
1о D(y) = (−∞; 0)u(0; +∞)
2о E(y) = (−∞; 0)u(0 ; +∞)
3о Функция нечетная.
4о х ≠ 0, у ≠ 0.
5о Если k > 0, то функция убывает
при х(−∞; 0)u(0; +∞).
Если k < 0, то функция возрастает
при х(−∞; 0)u(0; +∞).

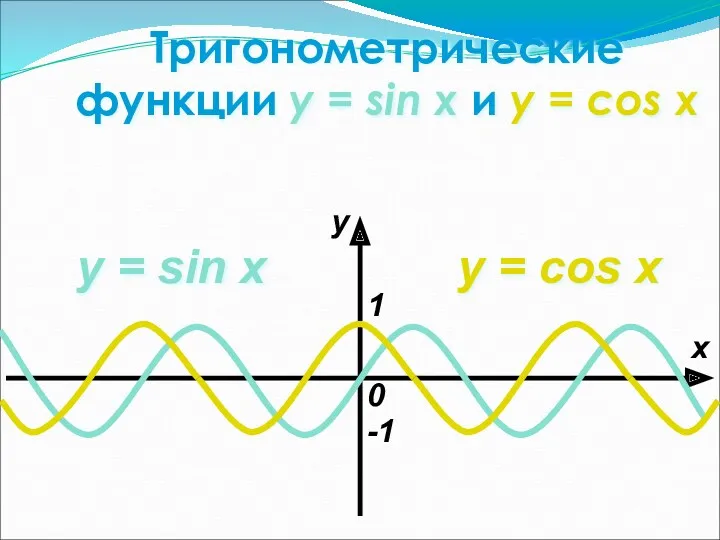
Тригонометрические
функции y = sin x и y = cos x
y = sin x
x
y
0
1
-1
y = cos x

Свойства функции
y = sin x
1о D(y)=(−∞; +∞).
2о E(y)=[−1; 1].
3о Функция нечетная.
4о Если х = 0, то у = 0.
5о Функция возрастает при
Функция убывает при
6о

Свойства функции
y = cos x
1о D(y)=(−∞; +∞).
2о E(y)=[−1; 1].
3о Функция четная.
4о Если х = 0, то у = 1.
5о Функция возрастает при х[−π+2πn;2πn], nZ.
Функция убывает при х[2πn; Π+2πn], где nZ.
6o xmax = 2πn; xmin = π+2πn, где nZ.

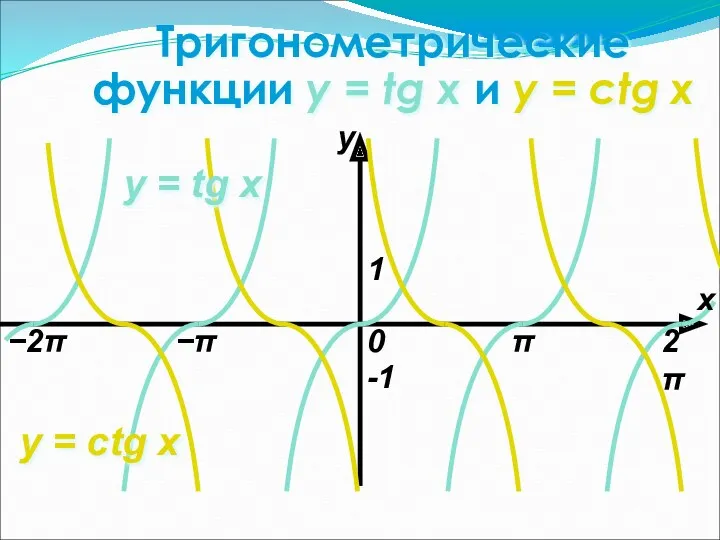
Тригонометрические
функции y = tg x и y = ctg x
0
1
-1
y = ctg x
y = tg x
у
π
−π
−2π
2π
x

Свойства функции
y = tg x
1о D(y)= где nZ.
2о E(y)=(−∞; +∞).
3о Функция нечетная.
4о Если х = 0, то у = 0.
5о Функция возрастает при х
где nZ.
6o Экстремумов нет.

Свойства функции
y = ctg x
1о D(y)=(πn; π+πn), где nZ
2о E(y)=(−∞; +∞).
3о Функция нечетная.
4о х ≠ 0; у = 0 если х , где nZ.
5о Функция убывает при х(πn; π+πn), где nZ.
6o Экстремумов нет.

Преобразование графиков
Параллельный перенос на вектор (0;b) вдоль оси ординат.
Для построения графика функции f(x)+b, где b – постоянное число, надо перенести график f на вектор (0;b) вдоль оси ординат.

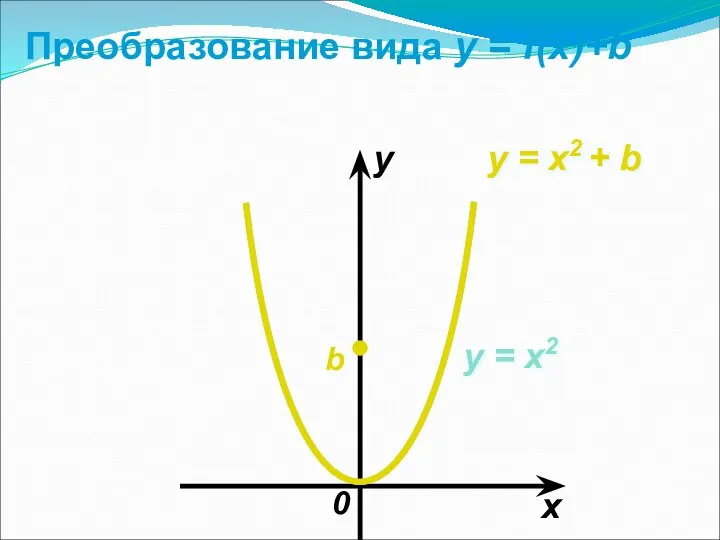
Преобразование вида y = f(x)+b
— Это параллельный перенос графика функции y = f(x) на b единиц вдоль оси ординат
Если b > 0, то
происходит
Если b < 0, то
происходит

Преобразование вида y = f(x)+b
x
y
0
b
y = x2
y = x2 + b

Растяжение вдоль оси Оу с коэффициентом k
Для построения графика функции y=kf(x) надо растянуть график функции y=f(x) в k раз вдоль оси ординат.

Замечание. Если 0<|k|<1, то растяжение с коэффициентом k часто называют сжатием.

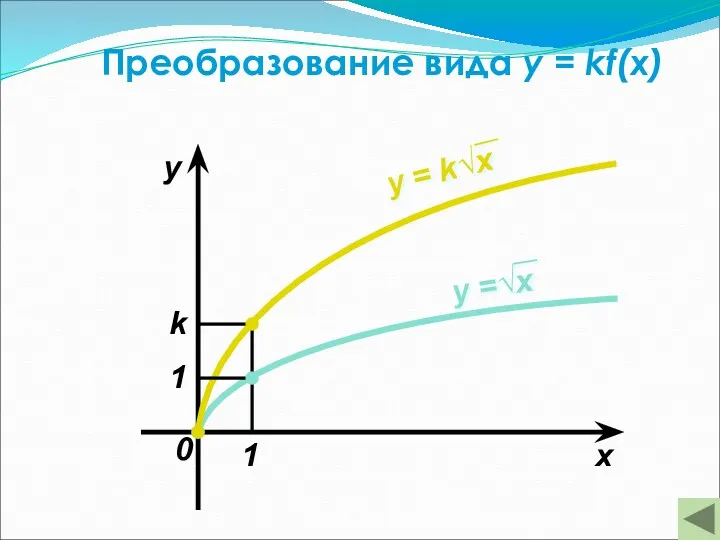
Преобразование вида y = kf(x)
— Это растяжение (сжатие) в k раз
графика функции y = f(x)
вдоль оси ординат
Если , |k| > 1, то
происходит
Если , |k| < 1, то происходит

Преобразование вида y = kf(x)
x
y
1
1
k
0

Параллельный перенос вдоль оси абсцисс на вектор (а;0)
График функции y=f(x-a) получается из графика f переносом (вдоль оси абсцисс) на вектор (а;0).
Если а>0, то вектор (а;0) направлен в положительном направлении оси абсцисс, а при a<0 – в отрицательном.

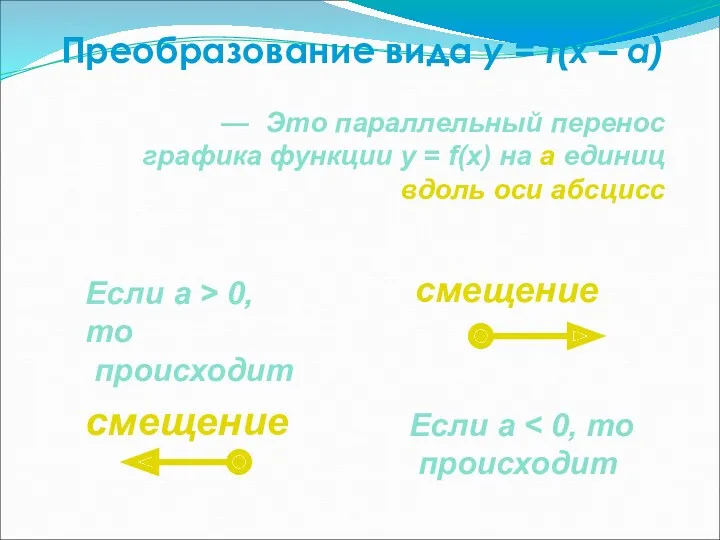
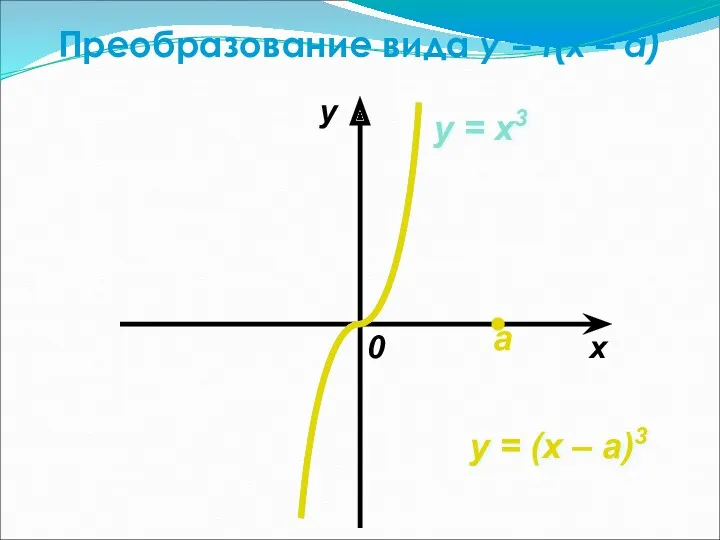
Преобразование вида y = f(x – a)
— Это параллельный перенос
графика функции y = f(x) на а единиц вдоль оси абсцисс
Если а > 0, то
происходит
Если а < 0, то
происходит

Преобразование вида y = f(x – a)
x
y
0
y = (x – a)3
y = x3
a

Растяжение вдоль оси Ох с коэффициентом k
Для построения графика функции
надо подвергнуть график функции f растяжению с коэффициентом k вдоль оси абсцисс.

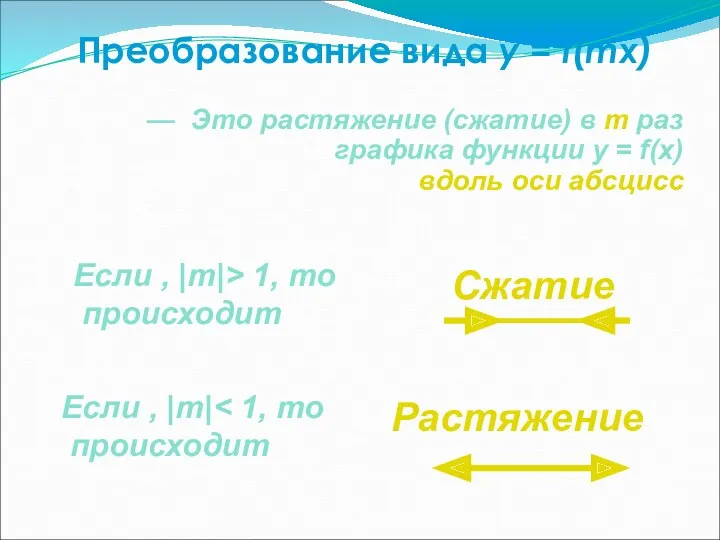
Преобразование вида y = f(mx)
— Это растяжение (сжатие) в m раз графика функции y = f(x) вдоль оси абсцисс
Если , |m|> 1, то
происходит
Если , |m|< 1, то
происходит

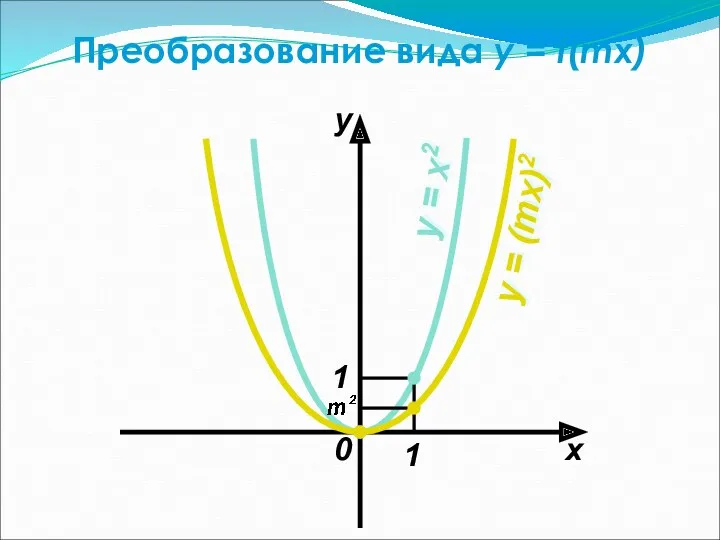
Преобразование вида y = f(mx)
0
x
y
1
1
y = x2
y = (mx)2

Тригонометрические функции,
их свойства и графики

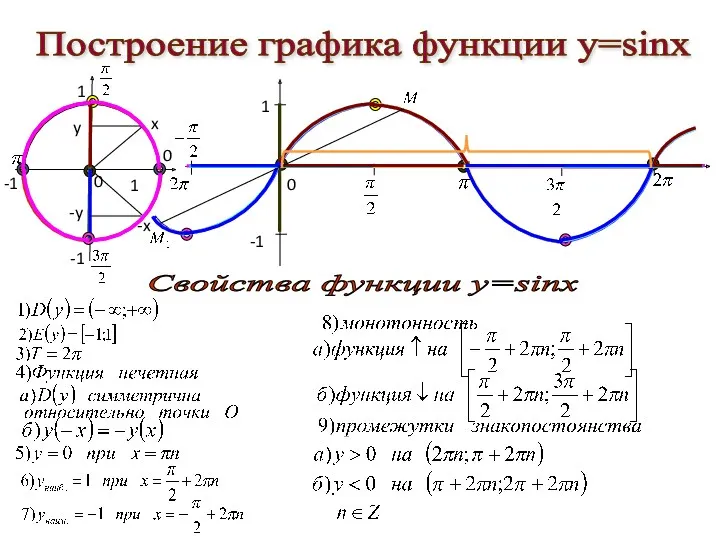
Построение графика функции у=sinx
1
-1
0
0
0
Свойства функции у=sinx
x
-x
y
-y
1
-1
-1
1

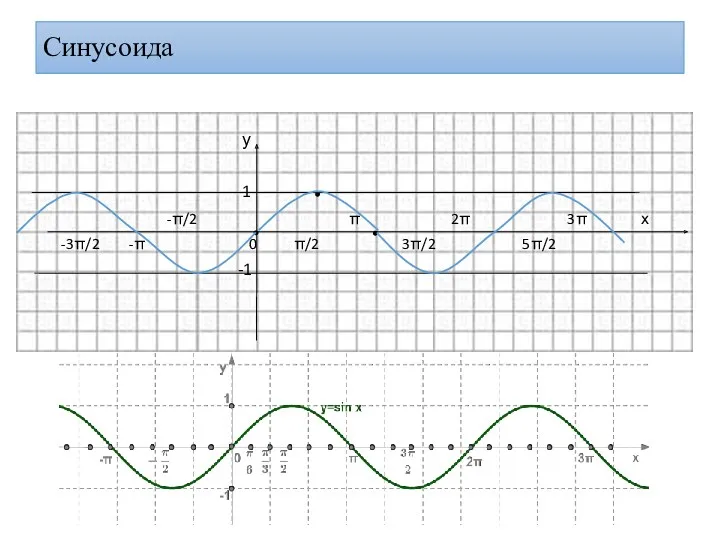
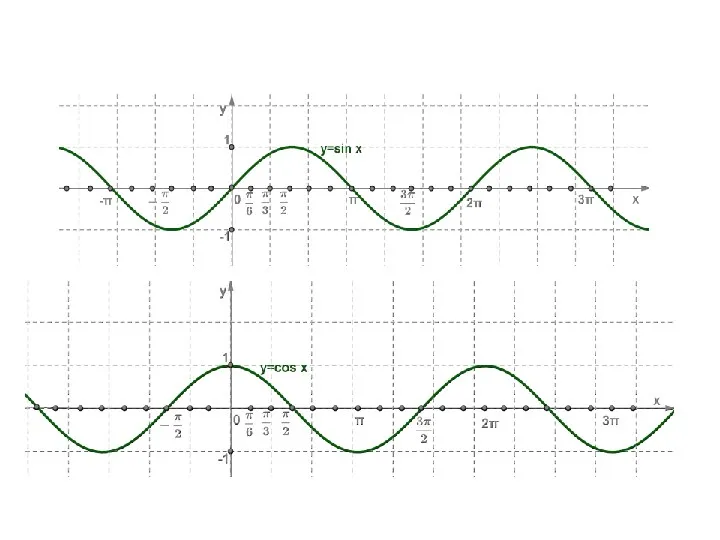
Синусоида
у
1
-π/2 π 2π 3π х
-3π/2 -π 0 π/2 3π/2 5π/2
-1

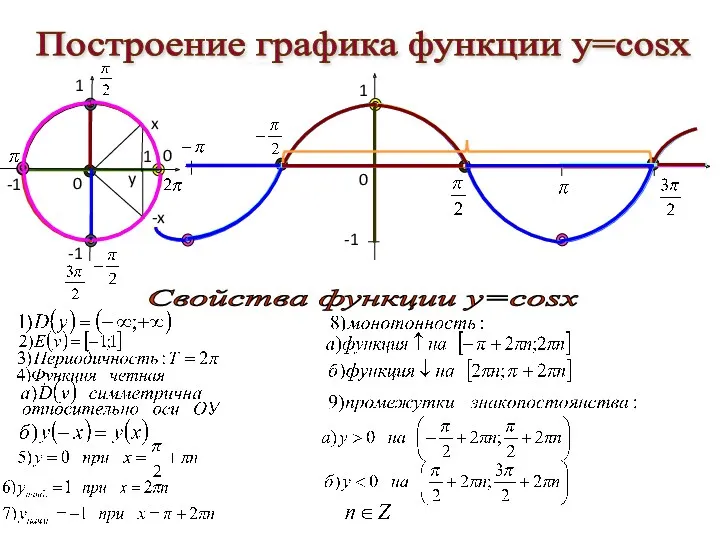
Построение графика функции у=cosx
1
-1
0
0
0
Свойства функции у=cosx
x
-x
1
-1
-1
1
y

Преобразование графиков функций y=sin x и y=cos x
Параллельный перенос вдоль оси Параллельный перенос вдоль оси OY
Параллельный перенос вдоль оси Параллельный перенос вдоль оси OX
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OX
Симметрия относительно оси абсцисс
Пример построения графика сложной функции

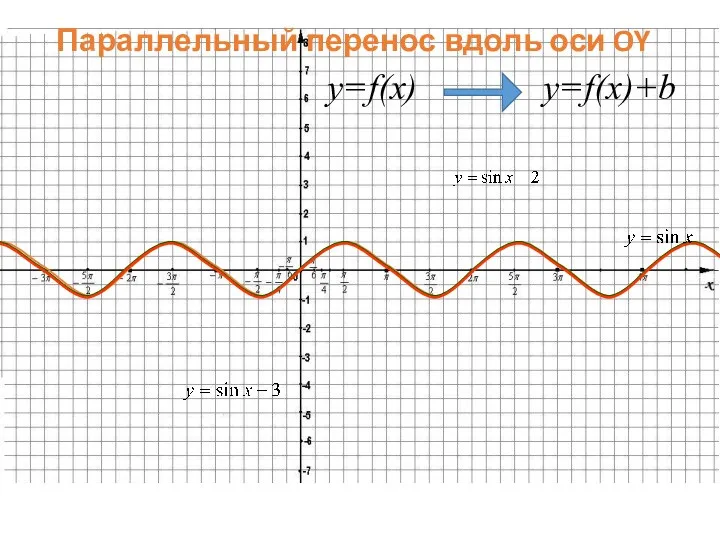
Параллельный перенос вдоль оси OY
y=f(x) y=f(x)+b

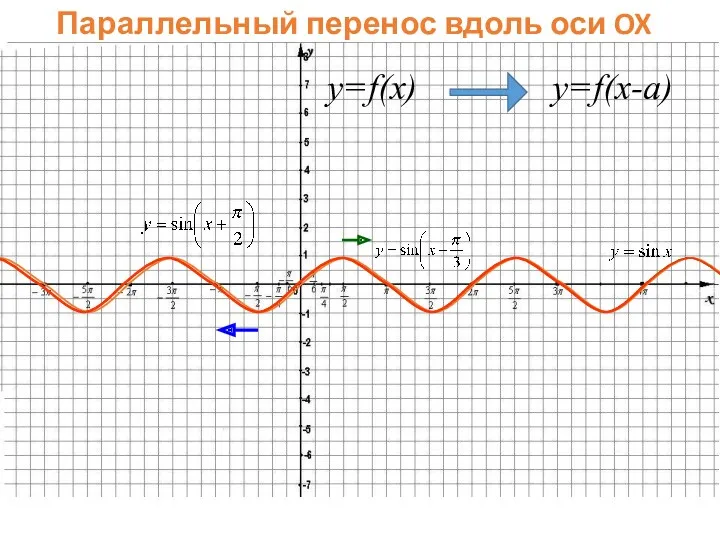
Параллельный перенос вдоль оси OX
y=f(x) y=f(x-a)

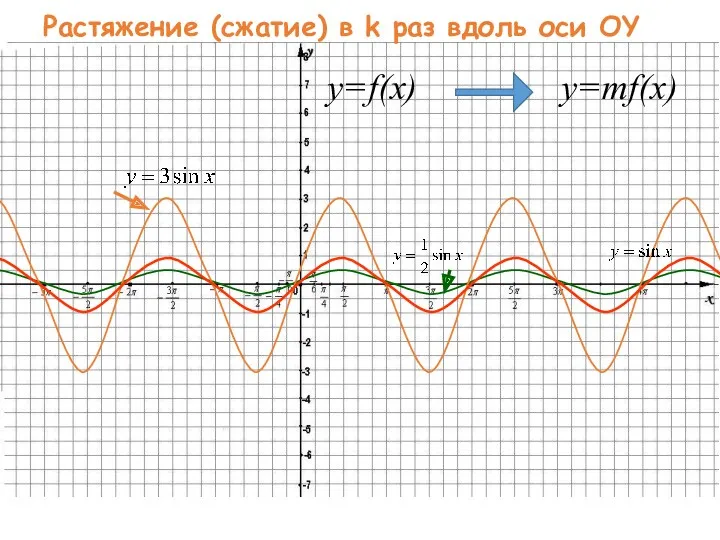
Растяжение (сжатие) в k раз вдоль оси OY
y=f(x) y=mf(x)

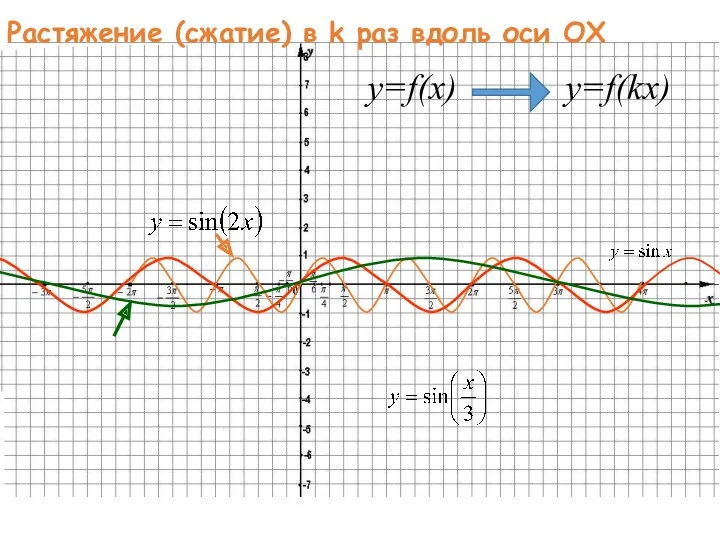
Растяжение (сжатие) в k раз вдоль оси OX
y=f(x) y=f(kx)

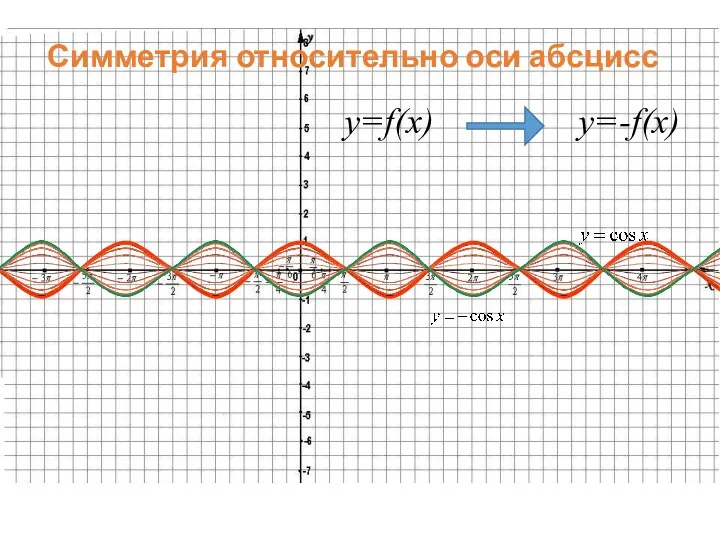
Симметрия относительно оси абсцисс
y=f(x) y=-f(x)

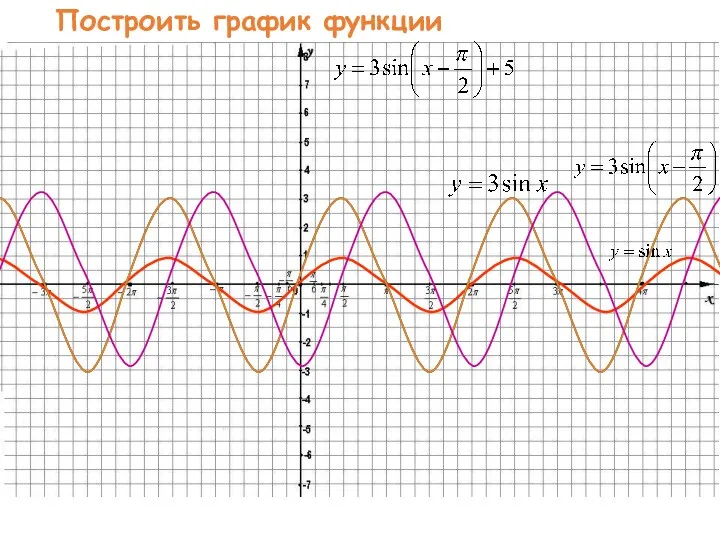
Построить график функции

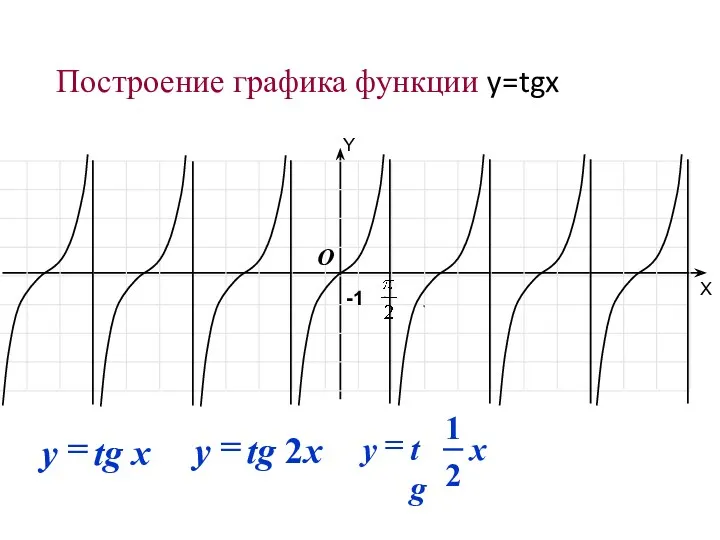
Построение графика функции y=tgx
-1
O
Y
X

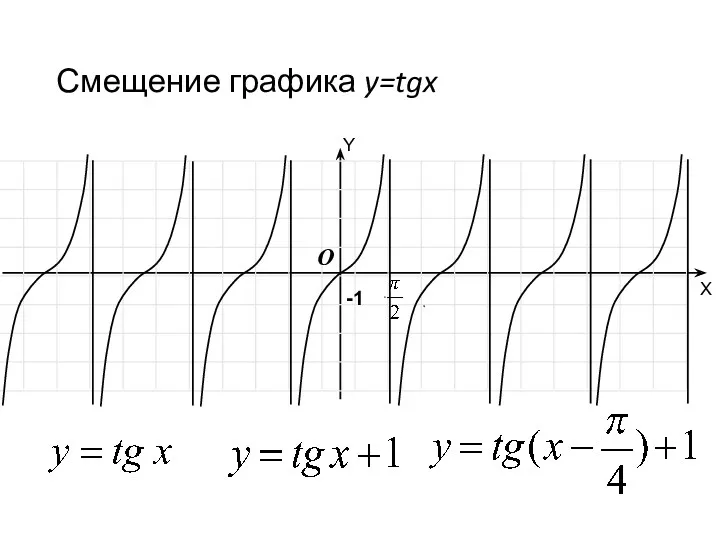
Смещение графика y=tgx
-1
O
Y
X

Свойства графика функции y=tg x
Область определения: x≠π/2+πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z

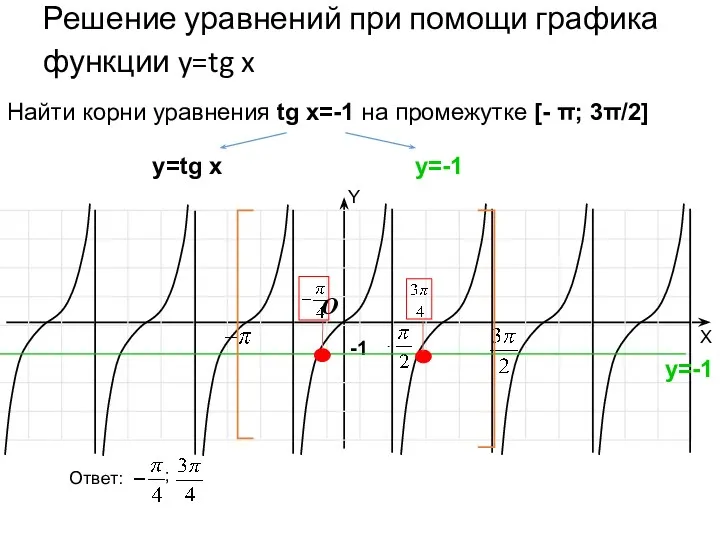
Решение уравнений при помощи графика функции y=tg x
-1
O
Найти корни уравнения tg x=-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Ответ:
;
Y
X
y=-1

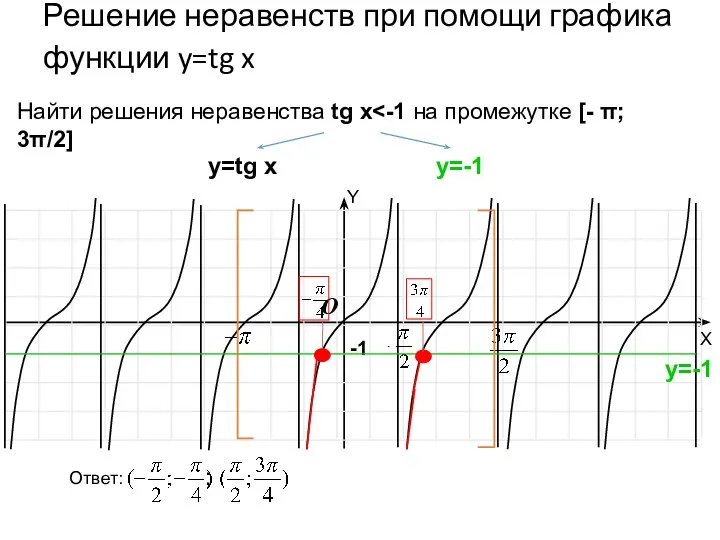
Решение неравенств при помощи графика функции y=tg x
-1
O
Найти решения неравенства tg x<-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Ответ:
;
Y
X
y=-1

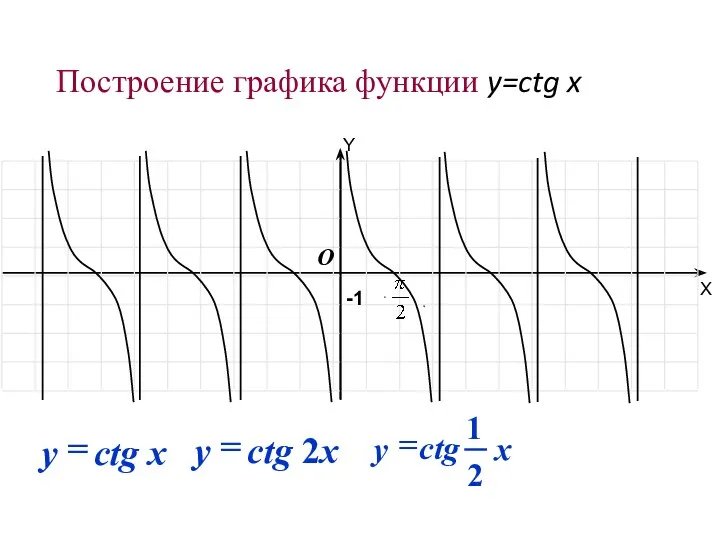
Построение графика функции y=ctg x
-1
O
Y
X

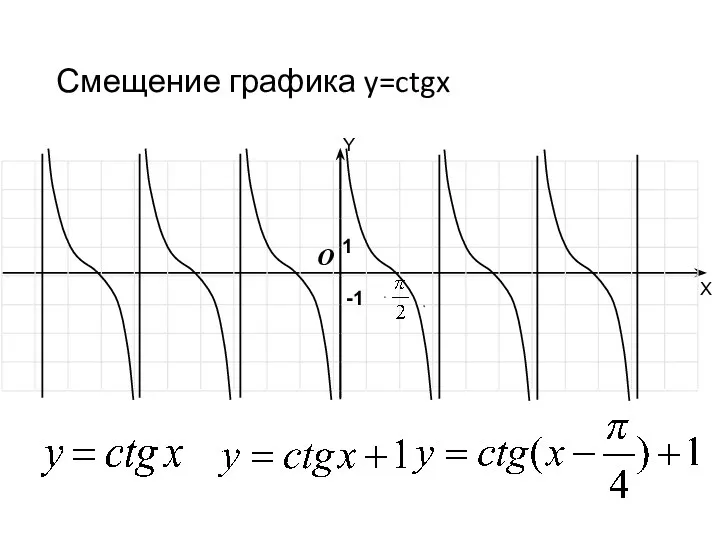
Смещение графика y=ctgx
-1
O
1
Y
X

Свойства графика функции y=ctg x
Область определения: x≠πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z

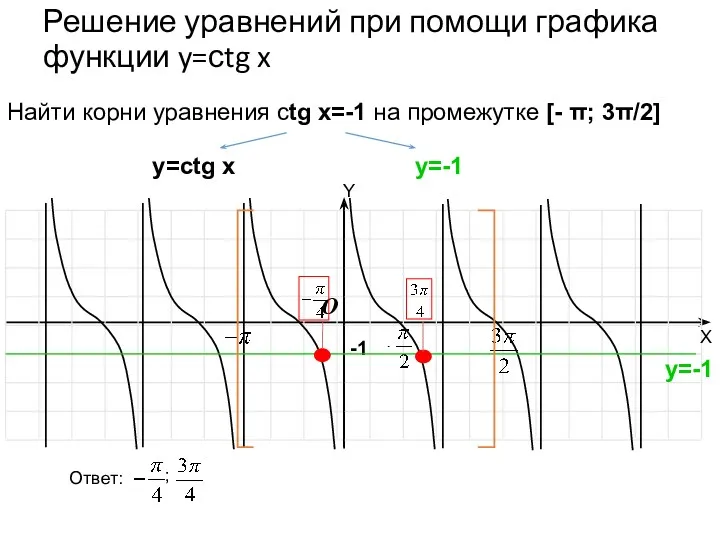
Решение уравнений при помощи графика функции y=сtg x
-1
O
Найти корни уравнения сtg x=-1 на промежутке [- π; 3π/2]
y=сtg x
y=-1
Ответ:
;
Y
X
y=-1