Содержание
- 2. Содержание Понятие производной. Алгоритм нахождения производной. Примеры. Таблица производных. Физический смысл производной. Правила нахождения производных. Непрерывность
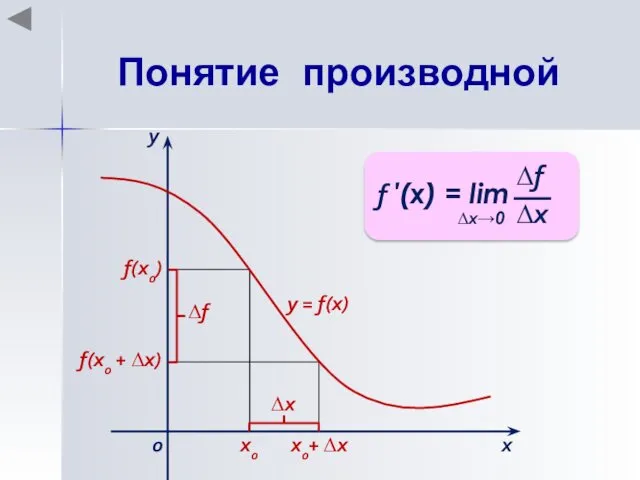
- 3. Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке
- 4. Понятие производной х0 х0+ ∆х f(x0) f(x0 + ∆х) ∆х х у 0 ∆f у =
- 5. Зафиксировать значение х0, найти f(x0). Дать аргументу х0 приращение ∆х, перейти в новую точку х0 +
- 6. Примеры 1. Найти производную функции y = kx + b в точке хo
- 7. Примеры 2. Найти производную функции y = C (C – const) в точке хo
- 8. Примеры 3. Найти производную функции y = x2 в точке хo
- 9. Примеры
- 10. Примеры
- 11. Примеры 5. Найти производную функции y = 1/x в точке хo
- 12. Примеры 5. Найти производную функции y = 1/x в точке хo
- 13. Таблица производных
- 14. Физический ( механический ) смысл производной Если при прямолинейном движении путь s, пройденный точкой, есть функция
- 15. Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 16. Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 17. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 18. Производная сложной функции (f(g(x)))′ = f′(g(x))∙g′(x) Примеры: 1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x –
- 20. Скачать презентацию
















 Симметрия. Осевая симметрия
Симметрия. Осевая симметрия Подготовка к ОГЭ-2021г. Задание 10. Теория вероятности. 9 класс
Подготовка к ОГЭ-2021г. Задание 10. Теория вероятности. 9 класс Основное свойство дроби
Основное свойство дроби Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс
Сокращение дробей. Задание для устного счета. Упражнение 6. 6 класс Практическое применение подобия треугольников
Практическое применение подобия треугольников Непрерывная случайная величина. Равномерное, показательное и нормальное распределение
Непрерывная случайная величина. Равномерное, показательное и нормальное распределение Расчет количества материала необходимого для ремонта
Расчет количества материала необходимого для ремонта Умножение трёхзначного числа на однозначное
Умножение трёхзначного числа на однозначное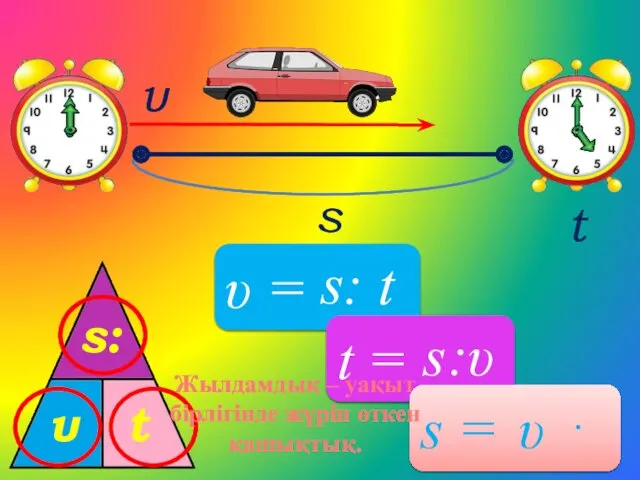 Жылдамдық. Уақыт. Қашықтық
Жылдамдық. Уақыт. Қашықтық Площадь многоугольников
Площадь многоугольников Наибольшее (наименьшее) значение показательной функции
Наибольшее (наименьшее) значение показательной функции Арифметические действия. Двузначные числа (устные вычисления).
Арифметические действия. Двузначные числа (устные вычисления). Тригонометричні функції числового аргументу. Алгебра. 10 клас
Тригонометричні функції числового аргументу. Алгебра. 10 клас Преобразование графиков функций
Преобразование графиков функций Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Определенный интеграл. Формула интегрирования по частям (пример 4)
Определенный интеграл. Формула интегрирования по частям (пример 4) Принцип Дирихле. Занимательные задачи
Принцип Дирихле. Занимательные задачи Разработка урока математики (3 класс) по теме Единицы массы
Разработка урока математики (3 класс) по теме Единицы массы О великом Пифагоре
О великом Пифагоре Треугольник. 6 класс
Треугольник. 6 класс Значения тригонометрических функций
Значения тригонометрических функций Шкалы и измерения
Шкалы и измерения Математическое описание Кубика Рубика
Математическое описание Кубика Рубика Линейная множественная регрессия
Линейная множественная регрессия Роль и место математики в современном мире
Роль и место математики в современном мире Формулы для подсчёта количества перестановок, сочетаний, размещений. Комбинаторика
Формулы для подсчёта количества перестановок, сочетаний, размещений. Комбинаторика Откладывание вектора от данной точки
Откладывание вектора от данной точки