Содержание
- 2. 1. Линейная модель множественной регрессии Если любая парная регрессия статистически незначима, то следует искать зависимость объясняемой
- 3. Множественный регрессионный анализ является обобщением парного, однако здесь появляются новые проблемы, из которых следует выделить две.
- 4. Вторая проблема связана с исследованием влияния конкретной независимой переменной на признак , т.е. разграничения её воздействия
- 5. Будем далее считать, что факторы отобраны правильно, а в качестве уравнения связи с признаком выбрана наиболее
- 6. Для построения модели требуются исходные статистические данные в виде следующей многомерной выборки ( ):
- 7. Тогда наблюдаемые значения переменных должны удовлетворять уравнению , (1) где значение признака в м наблюдении, значение
- 8. Оценкой уравнения (1) по выборке является выборочное уравнение регрессии . (2)
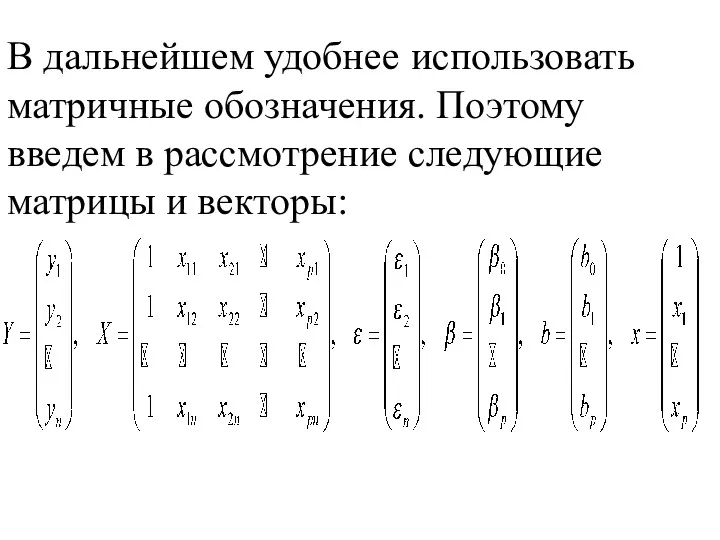
- 9. В дальнейшем удобнее использовать матричные обозначения. Поэтому введем в рассмотрение следующие матрицы и векторы:
- 10. Тогда уравнение регрессии (1) в матричной форме запишется а выборочное уравнение (2) примет вид . Отсюда
- 11. Чтобы получить оценку вектора методом наименьших квадратов, дополнительно к предпосылкам МНК для парной регрессии 1° -5°
- 12. При выполнении указанных предпосылок (1° - 6°) искомый вектор определяется из системы нормальных уравнений в матри-чной
- 13. 2. Ранжирование факторов Если бы все объясняющие переменные в уравнении (2) измерялись в одних и тех
- 14. Однако в общем случае переменные имеют различные единицы измерения и такое ранжирование невозможно (ошибочно). В этом
- 15. где средние квадратические отклонения переменных соответственно. Коэффициент показывает, на сколько в среднем изменится переменная , если
- 16. Имея значения , можно построить уравнение множественной регрессии в стандартизованном масштабе (6) где , стандартизованные переменные,
- 17. Чем больше модуль , тем сильнее влияние фактора на признак , т.е. по значениям можно выполнить
- 18. От уравнения вида (6) можно перейти к уравнению регрессии в натуральном масштабе (2), используя формулы:
- 19. Для оценки влияния отдельных факторов на переменную также можно использовать средние коэффициенты эластичности Ранжирование факторов по
- 20. Коэффициент частной корреляции характеризует тесноту линейной связи между признаком и фактором при устранении (элиминировании) влияния других
- 21. Например, частными коэффициентами корреляции являются: коэффициент первого порядка, учитывающий связь и фактора при неизменном действии фактора
- 22. Отсюда коэффициент парной корреляции можно рассматривать как частный коэффициент 0-го порядка. Коэффициенты частной корреляции более высоких
- 23. При этом существует связь между частными коэффициентами корреляции и стандартизованными коэффициентами регрессии:
- 24. 3. Оценка качества уравнения множественной регрессии По аналогии с парной регрессией можно определить долю результата ,
- 25. Величину называют коэффициентом множественной детерминации. Он служит измерителем качества подбора уравнения. Его значения изменяются в пределах
- 26. который представляет собой обобщение парного коэффициента корреляции и характеризует совместное (совокупное) влияние всех факторов на результат
- 27. Коэффициент является неубывающей функцией числа объясняющих переменных. Если добавить в модель фактор, который совсем не влияет
- 28. Доказано, что увеличивается при добавлении нового фактора в модель тогда и только тогда, когда модуль статистики
- 29. Проверка статистического качества модели выполняется путем проверки совокупной значимости её коэффициентов, т.е. проверки гипотезы: На практике
- 30. Для проверки данной гипотезы используется статистика: (7) которая имеет распределение Фишера.
- 31. Найденное по формуле (7) значение сравнивается с , которое находится по таблицам по заданному уровню значимости
- 32. Как и в случае парной регрессии выполняется статистическая значимость отдельных коэффициентов уравнения на основе статистик: (8)
- 33. Здесь диагональный элемент обратной матрицы , стоящий на пересечении й строки и го столбца; несмещенная оценка
- 34. Если , где находится из таблиц по значению и числу степеней свободы то коэффициент считается статистически
- 35. если , то статистически незначим; если , то относительно значим, и для уточнения следует воспользоваться строгой
- 36. Так же как и в парной регрессии для статистически значимых коэффициентов модели можно построить интервальные оценки:
- 37. Зафиксируем значения прогнозных объясняющих переменных и по вектору-столбцу найдем прогнозное значение зависимой переменной :
- 38. Тогда доверительный интервал для индивидуального прогнозного значения в точке примет вид где стандартная ошибка вычисляется по
- 39. 4. Частные критерии Не каждый фактор, дополнительно включаемый в модель, может существенно увеличить долю объясненной вариации
- 40. Мерой оценки значимости улучшения качества модели, в которой были включены факторы , после включения в неё
- 41. Если в модели 2, то используются два частных критерия: (9)
- 42. Фактические значения частных критериев , найденных по формуле (9), сравнивается с , определяемое по таблицам распределения
- 43. В противном случае дополнительное включение в модель фактора не увеличивает существенно долю объясненной вариации и, следовательно,
- 44. Пусть по наблюдениям построено уравнение регрессии с факторами и коэффициент множественной детерминации равен . Дополнительно в
- 45. Если , то гипотеза отклоняется и одновременное включение факторов в модель обоснованно. Если из модели одновременно
- 47. Скачать презентацию











































 Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла
Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла Корреляционный анализ данных. Лекция 9
Корреляционный анализ данных. Лекция 9 презентация по наглядной геометрии
презентация по наглядной геометрии Устный счет
Устный счет Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Диктанты на уроках геометрии в 8 классе
Диктанты на уроках геометрии в 8 классе Презентация к уроку математики 3 класс на тему Умножение трехзначного числа на однозначное
Презентация к уроку математики 3 класс на тему Умножение трехзначного числа на однозначное Предел функции
Предел функции Подобные треугольники. Пропорциональные отрезки
Подобные треугольники. Пропорциональные отрезки Свойства умножения натуральных чисел
Свойства умножения натуральных чисел Объем фигур
Объем фигур Кратчайшие пути из одной вершины в ориентированных ациклических графах. Алгоритм Дейкстры
Кратчайшие пути из одной вершины в ориентированных ациклических графах. Алгоритм Дейкстры Диференціальне числення. Похідна функції (лекція 1.2)
Диференціальне числення. Похідна функції (лекція 1.2) Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Математика в нашей жизни
Математика в нашей жизни Сетевые модели
Сетевые модели Неполные квадратные уравнения
Неполные квадратные уравнения Методики выполнения измерений, как основа метрологического обеспечения
Методики выполнения измерений, как основа метрологического обеспечения Математическая игра Поле чудес
Математическая игра Поле чудес Презентация Правильные и неправильные дроби
Презентация Правильные и неправильные дроби Формула корней квадратного уравнения
Формула корней квадратного уравнения компоненты сложения
компоненты сложения Сфера и шар
Сфера и шар Презентация к уроку математики Волшебные цифры Диск
Презентация к уроку математики Волшебные цифры Диск Методы проецирования. Проекции точки, проекции прямой (1 лекция)
Методы проецирования. Проекции точки, проекции прямой (1 лекция) Решение задач, с помощью квадратных уравнений
Решение задач, с помощью квадратных уравнений Из опыта работы Развитие математических представлений средствами фольклора и художественного слова
Из опыта работы Развитие математических представлений средствами фольклора и художественного слова Параллельность в пространстве. (Графическая работа 2)
Параллельность в пространстве. (Графическая работа 2)