Кратчайшие пути из одной вершины в ориентированных ациклических графах. Алгоритм Дейкстры презентация
Содержание
- 2. Определения Ориентированный граф без циклов называется ориентированным ациклическим графом. Путь в графе — последовательность вершин, в
- 3. Постановка задачи В задаче поиска кратчайших путей полагаются известными множества вершин и ребер ориентированного или неориентированного
- 4. Способы решения Алгоритм Беллмана – Форда для общего случая, когда вес каждого из ребер может быть
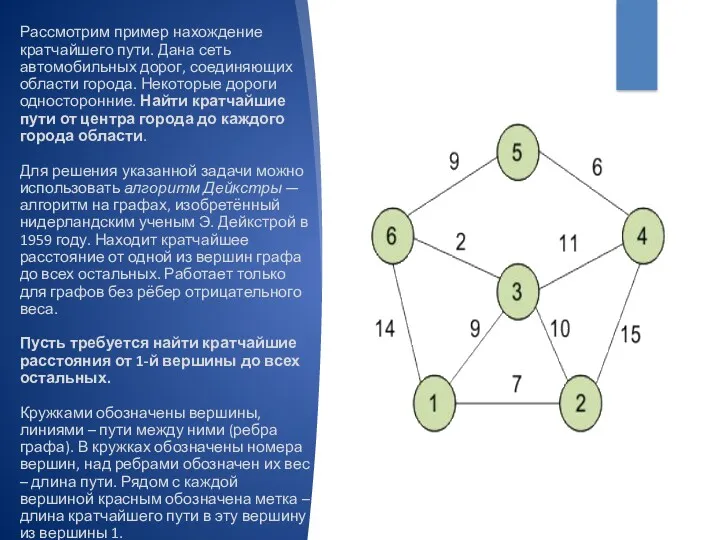
- 5. Рассмотрим пример нахождение кратчайшего пути. Дана сеть автомобильных дорог, соединяющих области города. Некоторые дороги односторонние. Найти
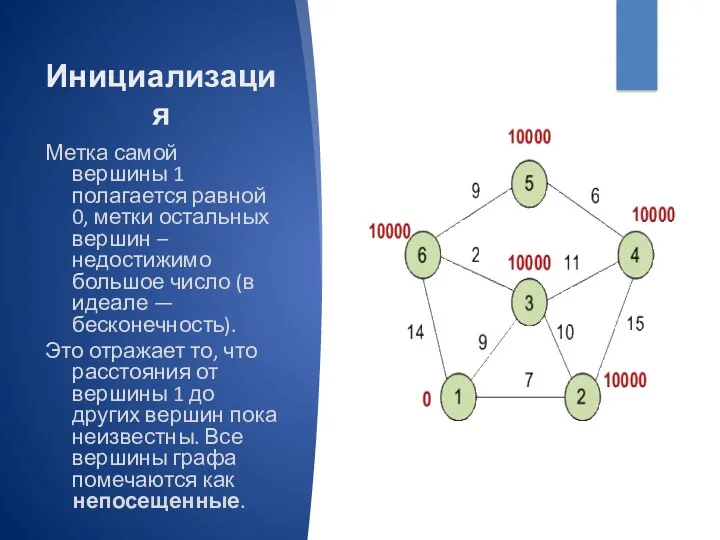
- 6. Инициализация Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в
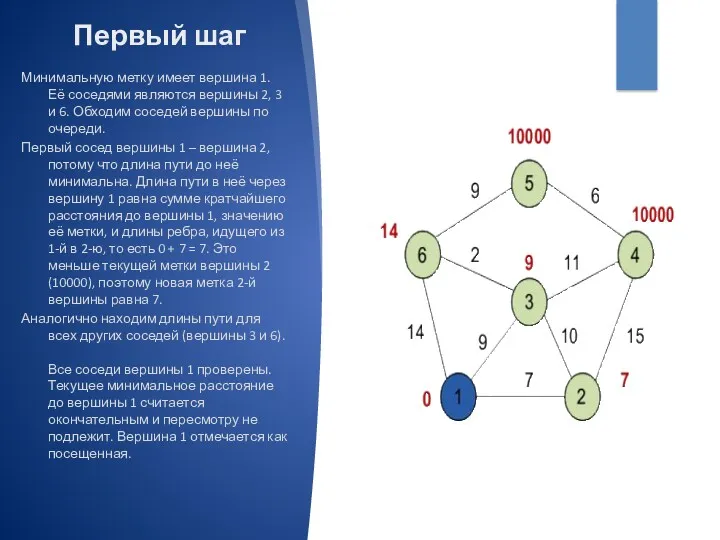
- 7. Первый шаг Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Обходим
- 8. Второй шаг Шаг 1 алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с
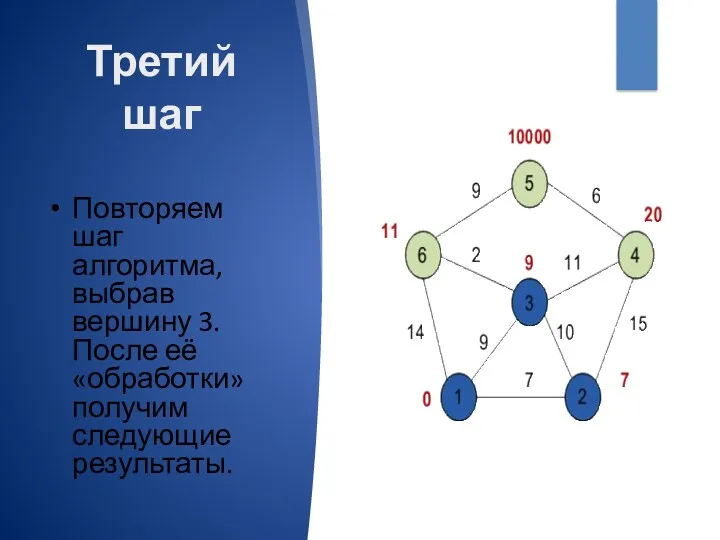
- 9. Третий шаг Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим следующие результаты.
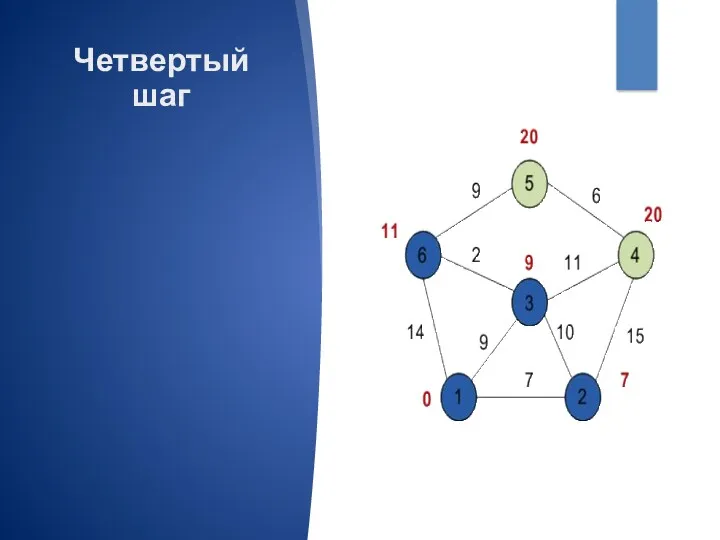
- 10. Четвертый шаг
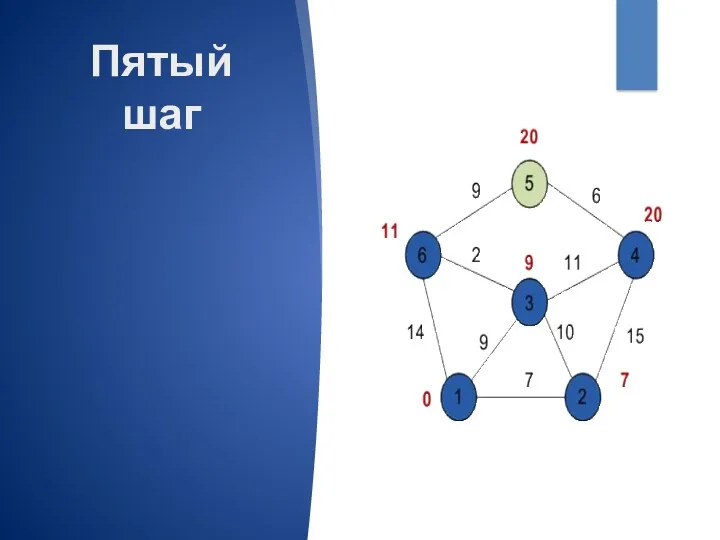
- 11. Пятый шаг
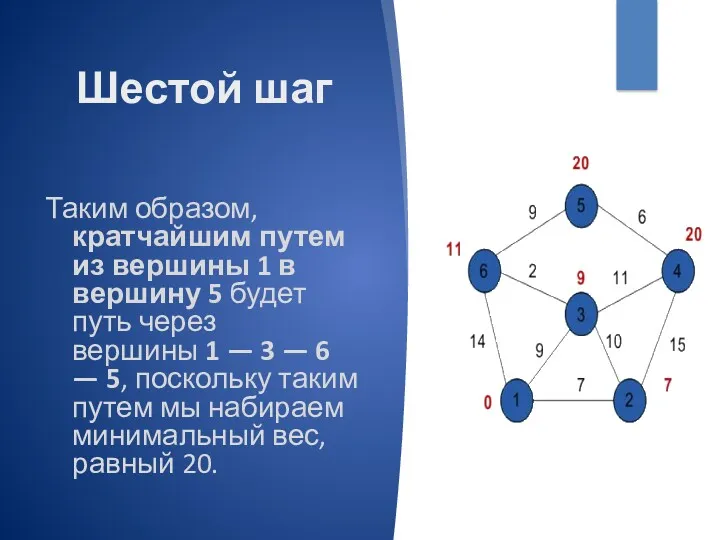
- 12. Шестой шаг Таким образом, кратчайшим путем из вершины 1 в вершину 5 будет путь через вершины
- 13. Вывод кратчайшего пути Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь
- 15. Скачать презентацию





 Биссектриса угла
Биссектриса угла Decimals
Decimals История космонавтики в цифрах
История космонавтики в цифрах Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Пик знаний
Пик знаний Презентация к уроку математики Сочетательное свойство умножения
Презентация к уроку математики Сочетательное свойство умножения Математики и математика в годы Великой Отечественной войны
Математики и математика в годы Великой Отечественной войны ДУ высших порядков. Задача Коши для уравнения порядка n
ДУ высших порядков. Задача Коши для уравнения порядка n Треугольник. Правило треугольника
Треугольник. Правило треугольника Обучение решению арифметических задач
Обучение решению арифметических задач Статическая детерминированная модель с дефицитом
Статическая детерминированная модель с дефицитом ГИА - 2012. Открытый банк заданий по математике. (Задача 8)
ГИА - 2012. Открытый банк заданий по математике. (Задача 8) Золотое сечение
Золотое сечение Разложение на простые множители
Разложение на простые множители Математический турнир для начальных классов
Математический турнир для начальных классов Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Математические диктанты
Математические диктанты Логические задачи 3 класс
Логические задачи 3 класс Методика моделирования дискретных и непрерывных случайных величин. Лекция 3
Методика моделирования дискретных и непрерывных случайных величин. Лекция 3 Определение декартовых координат. Координаты середины отрезка. Расстояние между точками
Определение декартовых координат. Координаты середины отрезка. Расстояние между точками Игра Что? Где? Когда?
Игра Что? Где? Когда? Признаки параллельности прямых
Признаки параллельности прямых Математика в жизни
Математика в жизни Конспект урока математики в 3 классе ТЕКСТОВЫЕ ЗАДАЧИ В ТРИ ДЕЙСТВИЯ
Конспект урока математики в 3 классе ТЕКСТОВЫЕ ЗАДАЧИ В ТРИ ДЕЙСТВИЯ Решение задач изученных видов.2 класс. УМК любой.
Решение задач изученных видов.2 класс. УМК любой. Знакомство с числом 0 и цифрой 0.
Знакомство с числом 0 и цифрой 0. Математические хитрости. Задачи. Урок 3.(2 класс)
Математические хитрости. Задачи. Урок 3.(2 класс)