Содержание
- 2. Вопрос 1. Моделирование дискретных случайных величин 1.1. Алгоритм моделирования дискрет-ной случайной величины
- 3. Допустим, что нам нужно получить значения случайной величины (СВ) ξ со следующим распределением: (1.1)
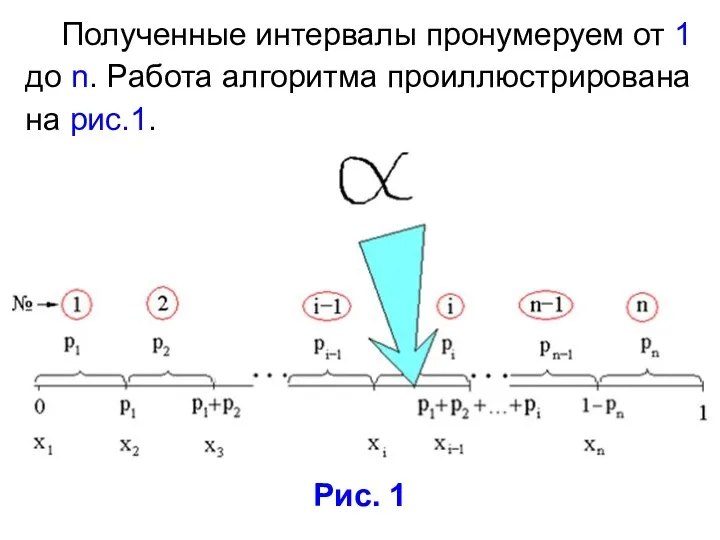
- 4. Разобьем отрезок [0;1] на n интервалов, длины которых равны соответственно: p1, p2, …, pn. Координатами точек
- 5. Полученные интервалы пронумеруем от 1 до n. Работа алгоритма проиллюстрирована на рис.1. Рис. 1
- 6. Рис. 2
- 7. Для получения значения дискретной СВ (ДСВ) ξ необходимо выбрать значение БСВ α и построить точку x
- 8. Так как БСВ α равномерно распределена в полуинтервале [0,1), то вероятность того, что α окажется в
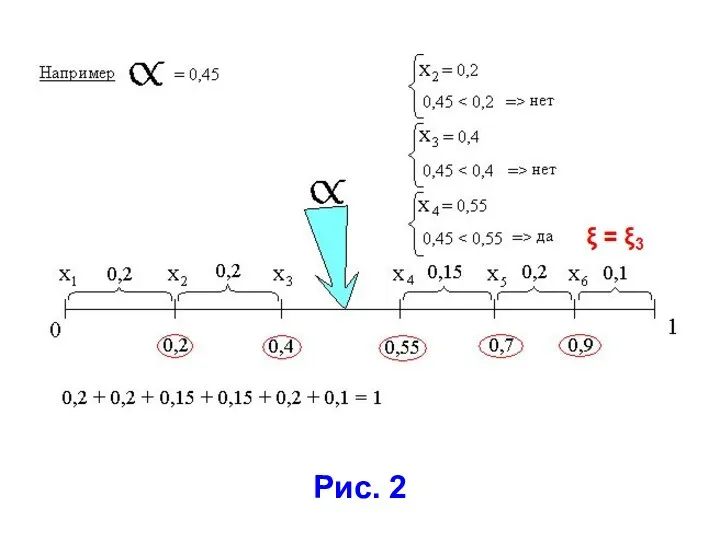
- 9. Согласно нашей процедуре ξ = ξi тогда, когда выполняется неравенство: (1.3) В правой части строгое неравенство,
- 10. 1.2. Моделирование полной группы случайных событий Определение. Совокупность событий называется полной группой случайных событий, если: а)
- 11. Пример. В случайном эксперименте по бросанию монеты полную группу образуют два события: А1 – "выпадение орла";
- 12. 1.3. Моделирование процесса случай-ного блуждания
- 13. Пусть ξt – случайный процесс с дискретным временем τ = m·Δt (m = 0,1,…) и дискретным
- 14. Пусть в момент времени t≥0 процесс находится в состоянии x, т.е. ξt=x, а в следующий момент
- 15. Согласно (1.4) можно записать: (1.5) – ДСВ с распределе-нием вероятностей (1.6)
- 16. Тогда моделирование процесса ξt сводится к моделированию в каждый момент времени t+Δt реализации СВ ηt и
- 17. Вопрос 2. Моделирование непрерывных случайных величин 2.1. Метод обратной функции
- 18. При построении имитационной модели сложной системы часто необходимо моделировать непрерывную СВ (НСВ) с заданной плотностью распределения
- 19. В некоторых случаях для решения данных задач применяют метод обратной функции. Рассмотрим функцию распределения случайной величины:
- 20. Обозначим через x=F-1(y) функцию, обратную функции F(x). Теорема. Если α – базовая случайная величина, то случайная
- 21. Моделирующий алгоритм, реализующий метод обратной функции, включает следующие этапы: 1) нахождение функции распределения F(x) по заданной
- 22. Пример 1. Дана плотность экспоненциального распределения:
- 23. (2.2) 1) Определяем функцию экспоненциаль-ного распределения: 2) Определяем обратную функцию: (2.3)
- 24. (2.4) 3) Для моделирования экспоненциально-распределенной СВ ξ используем формулу: Так как величины α и 1-α одинаково
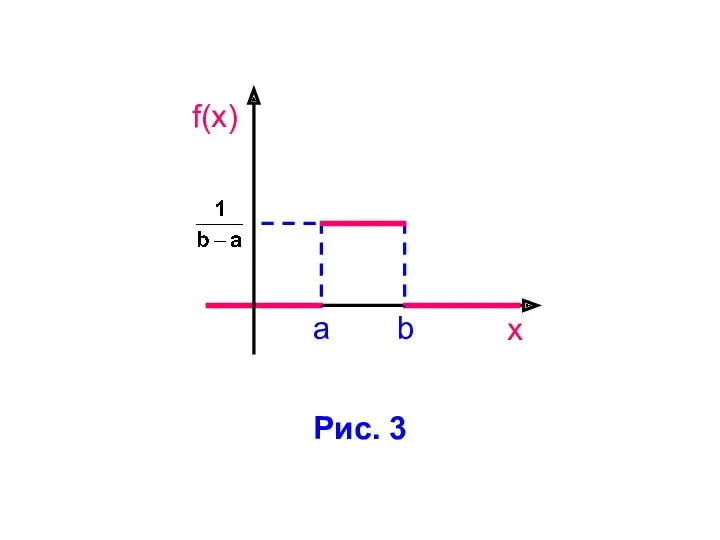
- 25. Пример 2. Дана плотность равномерного распреде-ления: (2.5)
- 26. Рис. 3
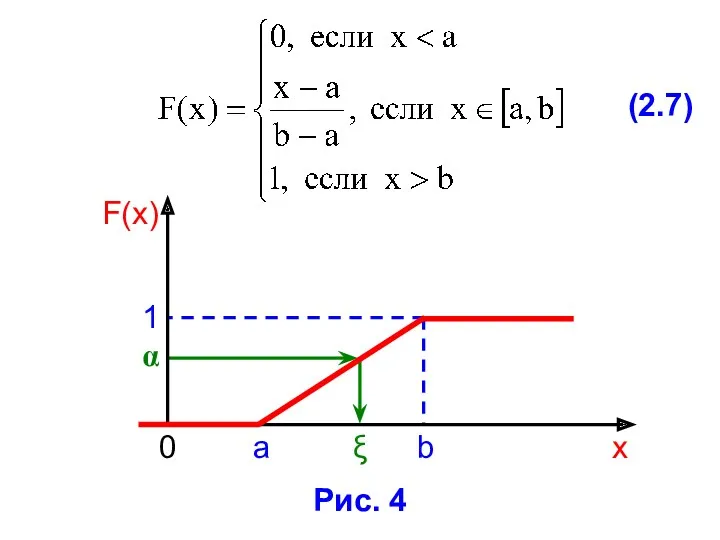
- 27. (2.6) 1) Определяем функцию равномерного распределения:
- 28. (2.7) Рис. 4
- 29. 2) Определяем обратную функцию: (2.8) (2.9) 3) Для моделирования равномерно-распределенной СВ ξ используем формулу: где α
- 30. 2.2. Метод исключения Используется в тех случаях, когда плотность распределения f(x) моделируемой СВ ξ имеет сложный
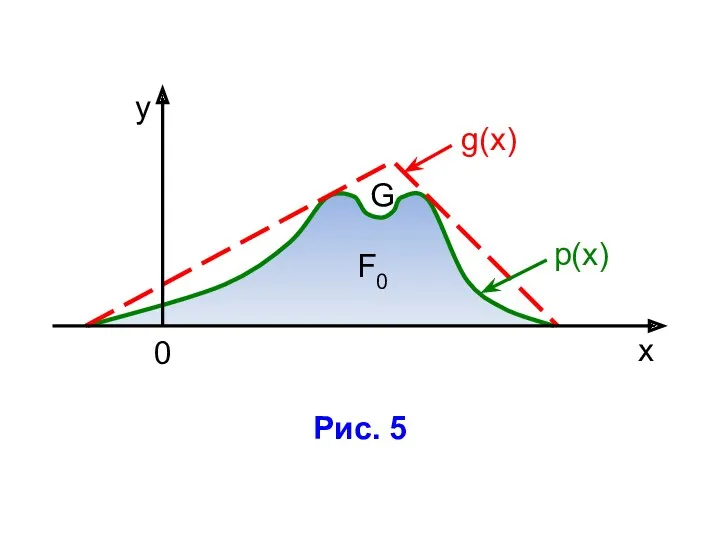
- 31. Рис. 5
- 32. Обозначим: F0 = { (x,y); 0≤y≤p(x) } – область, ограниченную кривой y=p(x) и осью абсцисс (рис.
- 33. Область G охватывает (мажорирует) область F0. Функция g(x) должна иметь значительно более простой, чем p(x) аналитический
- 34. Моделирующий алгоритм включает следующие этапы: 1) подбор мажорантной функции g(x) для заданной p(х); 2) моделирование случайного
- 35. 3) проведение следующей процедуры: если (х,у) – реализация вектора (ξ,η) и у≤p(х) (т.е. точка (х,у) попадает
- 36. Повторяя алгоритм многократно, получаем требуемое число реализаций случайной величины ξ.
- 37. 2.3. Метод суперпозиции (композиции) При достаточно сложном виде функции p(x) моделирование равномерного распре-деления в области F0
- 38. При этом вероятности попадания в области равны их площадям. Используя данные вероятности, "разыгрывают" номер области, в
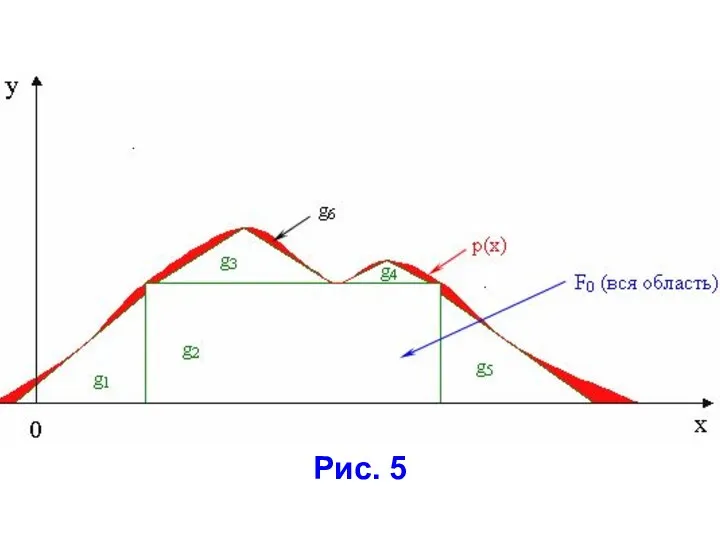
- 39. Рис. 5
- 40. На рис. 6 область F0 разбита на 5 простых областей, шестая – ограничена огибающей и данными
- 41. Для ускорения моделирования разбиение на области происходит так, чтобы части gi, имеющие наибольшую площадь (наибольшую вероятность
- 42. Этапы моделирующего алгоритма: 1) разбиение F0 на геометрически простые области; 2) моделирование случайного вектора (ξ,η) с
- 44. Скачать презентацию


![Разобьем отрезок [0;1] на n интервалов, длины которых равны соответственно:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/605256/slide-3.jpg)
































 Измерение углов
Измерение углов Усеченная пирамида
Усеченная пирамида Викторина Час весёлой математики
Викторина Час весёлой математики Деление на трехзначное число
Деление на трехзначное число Трикутники в навколишньому світі
Трикутники в навколишньому світі Движение. Зеркальная симметрия
Движение. Зеркальная симметрия Внеклассное мероприятие Аукцион математических задач
Внеклассное мероприятие Аукцион математических задач Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Түзу мен жазықтық арасындағы бұрыш
Түзу мен жазықтық арасындағы бұрыш Математическая викторина для 5-7 класса
Математическая викторина для 5-7 класса Активизация познавательной деятельности учащихся на уроках математики и во внеурочное время
Активизация познавательной деятельности учащихся на уроках математики и во внеурочное время Нахождение части от целого и целого по его части
Нахождение части от целого и целого по его части Викторина Час веселой математики
Викторина Час веселой математики Сравнение, сложение, вычитание дробей. Задание для устного счета
Сравнение, сложение, вычитание дробей. Задание для устного счета Элементы статистики. Статистические характеристики
Элементы статистики. Статистические характеристики Қаржы-несие шешімдерін қабылдауға қаржы-экономикалық есептеудің математикалық негіздері
Қаржы-несие шешімдерін қабылдауға қаржы-экономикалық есептеудің математикалық негіздері Системы уравнений как математические модели реальных ситуаций
Системы уравнений как математические модели реальных ситуаций Координаты вектора
Координаты вектора Пирамида. Виды пирамид. Решение задач
Пирамида. Виды пирамид. Решение задач Играем с Машей и медведем
Играем с Машей и медведем Числа от 11 до 20. Нумерация
Числа от 11 до 20. Нумерация Пропорция. Урок математики в 6 классе
Пропорция. Урок математики в 6 классе Презентация Устный счет
Презентация Устный счет Определение производной
Определение производной Схемная надежность
Схемная надежность Письменное умножение на числа, оканчивающиеся нулями
Письменное умножение на числа, оканчивающиеся нулями Практика по темам Последовательность и Арифметическая прогрессия
Практика по темам Последовательность и Арифметическая прогрессия Доли. Обыкновенные дроби
Доли. Обыкновенные дроби