Содержание
- 2. Определение поверхности второго порядка Поверхность, определяемая уравнением где A,B, … H - действительные числа, причем старшие
- 3. ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ Определение цилиндрической поверхности Уравнение цилиндрической поверхности Эллиптический цилиндр Гиперболический цилиндр Параболический цилиндр
- 4. Определение цилиндрической поверхности Поверхность, образованная всеми прямыми, проходящими параллельно данной прямой через точки линии , называется
- 5. Уравнение цилиндрической поверхности, с образующими параллельными оси OZ Пусть на плоскости дана своим уравнением некоторая линия
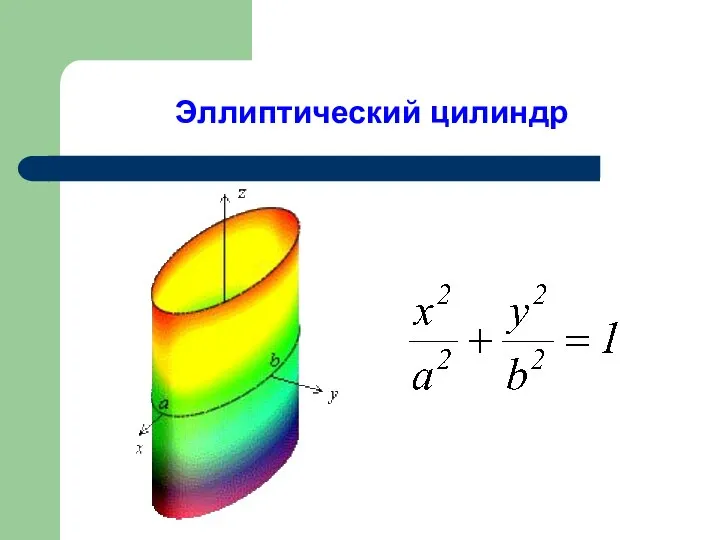
- 6. Эллиптический цилиндр
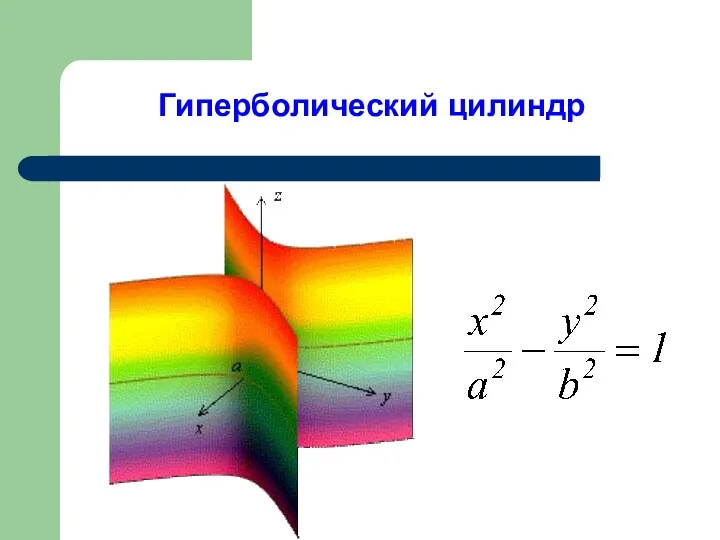
- 7. Гиперболический цилиндр
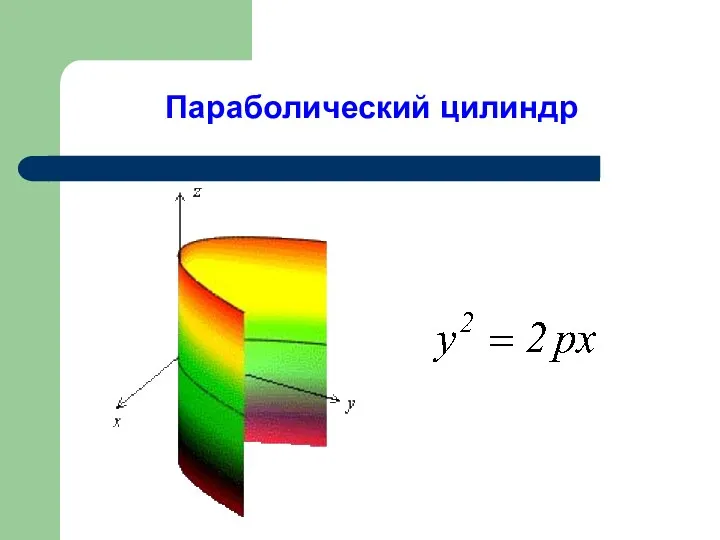
- 8. Параболический цилиндр
- 9. Эллиптический цилиндр, с образующими, параллельными оси OY Уравнение определяет эллиптический цилиндр с образующими, параллельными оси
- 10. Гиперболический цилиндр, с образующими, параллельными оси OX уравнение определяет гиперболический цилиндр с образующими, параллельными оси .
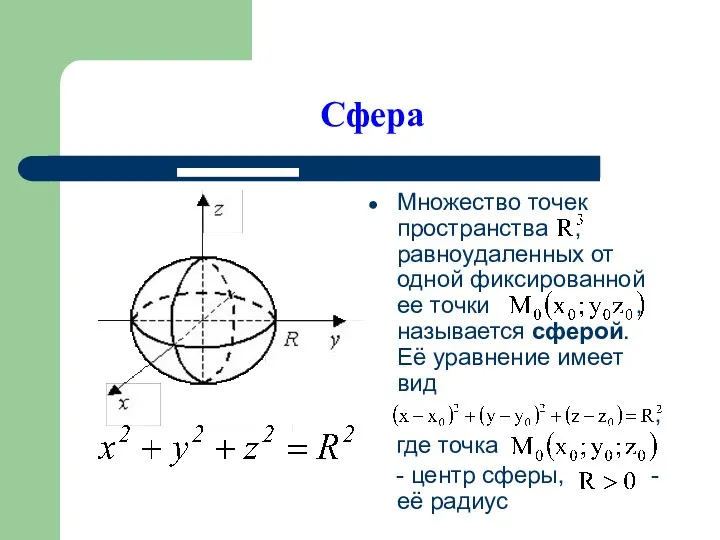
- 11. Сфера Множество точек пространства , равноудаленных от одной фиксированной ее точки , называется сферой. Её уравнение
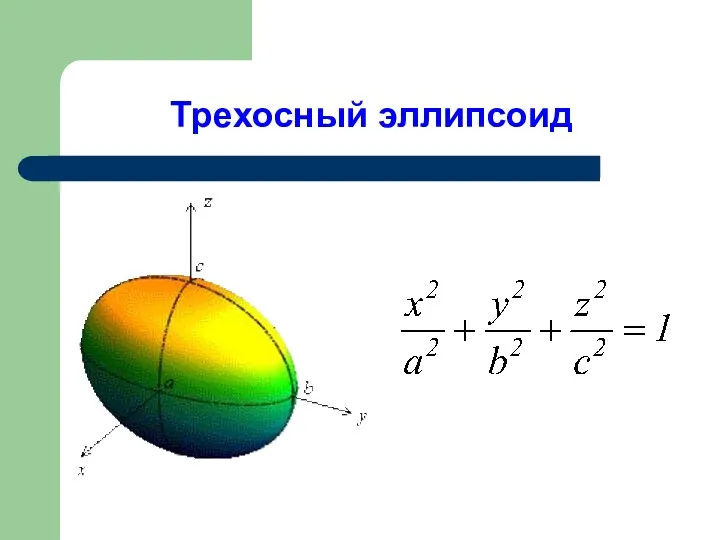
- 12. Трехосный эллипсоид
- 13. Рассмотрим вначале линии пересечения этой поверхности с горизонтальными плоскостями , где . В сечении, в общем
- 14. Сечение эллипсоида плоскостями z=h, при IhI>c Горизонтальные плоскости , где , не пересекают данной поверхности (в
- 15. Сечение эллипсоида плоскостями z=h, при IhI=c Рассмотрим сечение Горизонтальной плоскостью , где , то Следовательно, в
- 16. Сечение эллипсоида плоскостью z=h,при IhI Если , то . Тогда в сечении горизонтальной плоскостью , где
- 17. Сечение эллипсоида плоскостями x=h и y=h Так как уравнение обладает симметрией относительно переменных и , то
- 18. Эллиптический параболоид Эллиптическим параболоидом называется поверхность, определяемая уравнением , где При уравнение называется каноническим уравнением эллиптического
- 19. Сечение эллиптического параболоида плоскостями z=h Рассмотрим сечения поверхности горизонтальными плоскостями , где . В сечении, в
- 20. Сечение эллиптического параболоида плоскостями z=h, при h Так как по условию и , то при любых
- 21. Сечение эллиптического параболоида плоскостями z=h, при h=0 и h>0 При , то есть на плоскости ,
- 22. Сечение эллиптического параболоида плоскостями y=h Рассмотрим сечение вертикальной плоскостью , где . В сечении получим линию:
- 23. Параболоид вращения Если в уравнении , то в сечениях горизонтальными плоскостями образуются окружности. Следовательно, уравнение определяет
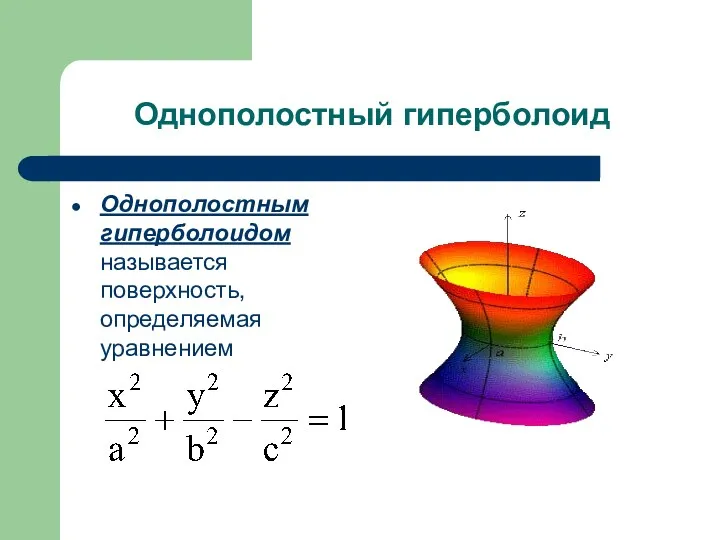
- 24. Однополостный гиперболоид Однополостным гиперболоидом называется поверхность, определяемая уравнением
- 25. Сечение однополостного гиперболоида плоскостями z=h В сечениях горизонтальными плоскостями , где , получим линии где .
- 26. Сечение однополостного гиперболоида плоскостями y=h, при IhI Пусть , где . В сечениях образуются линии Если
- 27. Сечение однополостного гиперболоида плоскостями y=h, при IhI>b Если , то . Тогда на плоскости получим гиперболу
- 28. Сечение однополостного гиперболоида плоскостями y=h, при IhI=b Если , то . Тогда из уравнения получим пару
- 29. Сечение однополостного гиперболоида плоскостями x=h В сечениях вертикальными плоскостями , где , образуются так же, как
- 30. Двуполостный гиперболоид Двуполостным гиперболоидом называется поверхность, заданная уравнением
- 31. Сечение двуполостного гиперболоида плоскостями z=h, при IhI Рассмотрим сечения горизонтальными плоскостями , где . В сечениях
- 32. Сечение двуполостного гиперболоида плоскостями z=h, при IhI=c Если , то Следовательно, в сечениях плоскостями и образуется
- 33. Сечение двуполостного гиперболоида плоскостями z=h, при IhI>c Если , то . Следовательно, первое уравнение из можно
- 34. Сечение двуполостного гиперболоида плоскостями y=h Пусть , где . Тогда в сечениях, получим линии Следовательно, на
- 35. Сечение двуполостного гиперболоида плоскостями x=h В сечениях вертикальными плоскостями , где , так же образуются гиперболы,
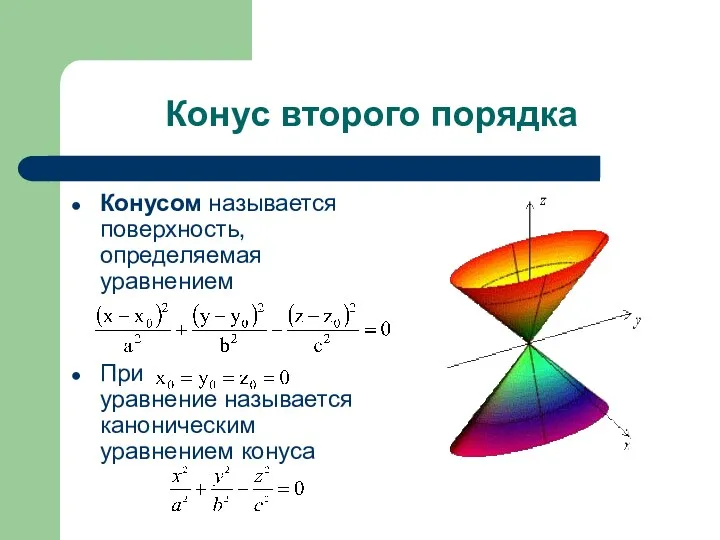
- 36. Конус второго порядка Конусом называется поверхность, определяемая уравнением При уравнение называется каноническим уравнением конуса
- 37. Конусы второго порядка с осями симметрии OX и OY Конусы с осями симметрии и соответственно задаются
- 39. Скачать презентацию





























 Решение текстовых задач. Задание В13, ЕГЭ
Решение текстовых задач. Задание В13, ЕГЭ презентация по математике
презентация по математике Формулы квадрата суммы и разности
Формулы квадрата суммы и разности Первообразная функция и неопределенный интеграл. Методы интегрирования
Первообразная функция и неопределенный интеграл. Методы интегрирования Презентация
Презентация Основные понятия дискретной математики. Теория вероятности
Основные понятия дискретной математики. Теория вероятности Деление на трехзначное число
Деление на трехзначное число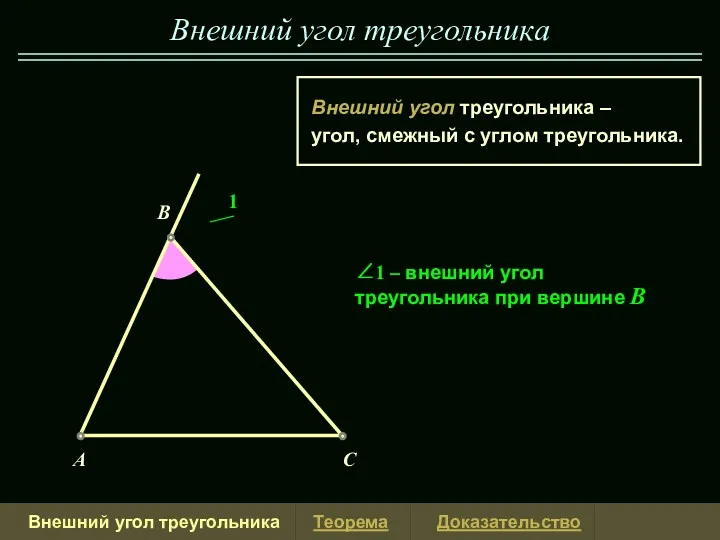 Внешний угол треугольника
Внешний угол треугольника Задачи на проценты
Задачи на проценты Функция нескольких переменных
Функция нескольких переменных Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. 8 класс Приведение подобных членов многочлена
Приведение подобных членов многочлена Математический аппарат физики
Математический аппарат физики Умножение чисел с разными знаками
Умножение чисел с разными знаками Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Решение треугольников
Решение треугольников Приём вычитания вида 12 -
Приём вычитания вида 12 - Урок повторения и обобщения по теме Свойства степени с натуральным показателем
Урок повторения и обобщения по теме Свойства степени с натуральным показателем Приемы деления основанные на связи между компонентами и результатом умножения
Приемы деления основанные на связи между компонентами и результатом умножения Применение производной для нахождения наилучшего решения в прикладных задачах
Применение производной для нахождения наилучшего решения в прикладных задачах Машина Тьюринга. Ограничения, свойственные МТ. Рекурсивность и теорема Геделя
Машина Тьюринга. Ограничения, свойственные МТ. Рекурсивность и теорема Геделя Признаки делимости на 3 и 9
Признаки делимости на 3 и 9 Логарифмическая функция
Логарифмическая функция Умножение и деление чисел с разными знаками. История космонавтики. 6 класс
Умножение и деление чисел с разными знаками. История космонавтики. 6 класс Конкурсный урок геометрии в 7 классе. Тема урока Треугольники
Конкурсный урок геометрии в 7 классе. Тема урока Треугольники Урок математики по теме: Числа от 1 до 10
Урок математики по теме: Числа от 1 до 10 Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Площадь фигур
Площадь фигур