Содержание
- 2. Содержание Четырехугольники Многоугольники Параллелограмм и трапеция Прямоугольник, ромб, квадрат 2. Площадь Площадь многоугольника Площадь параллелограмма, треугольника
- 3. Содержание 3. Подобные треугольники Определение подобных треугольников Признаки подобия треугольников Соотношения между сторонами и углами прямоугольного
- 4. Четырехугольники Многоугольники Параллелограмм и трапеция Прямоугольник, ромб, квадрат
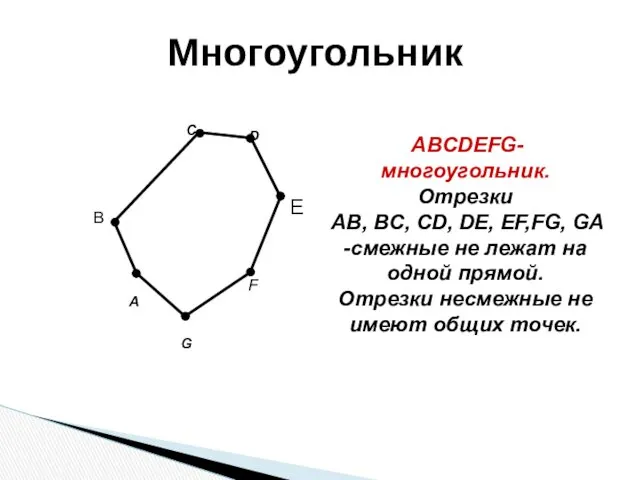
- 5. A C F G B ABCDEFG-многоугольник. Отрезки AB, BC, CD, DE, EF,FG, GA -смежные не лежат
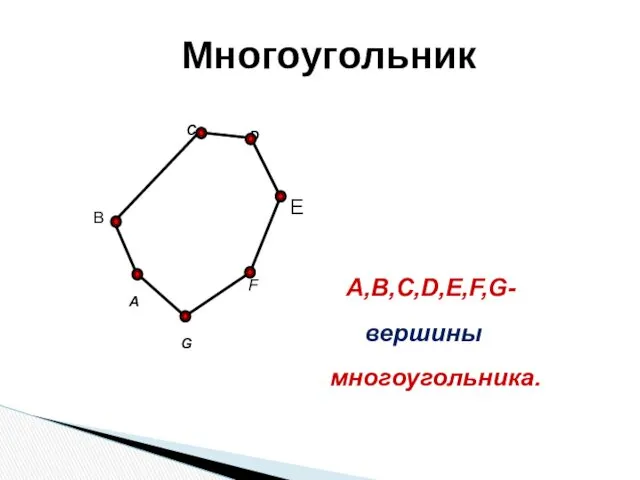
- 6. A C F G B A,B,C,D,E,F,G- многоугольника. D E вершины Многоугольник
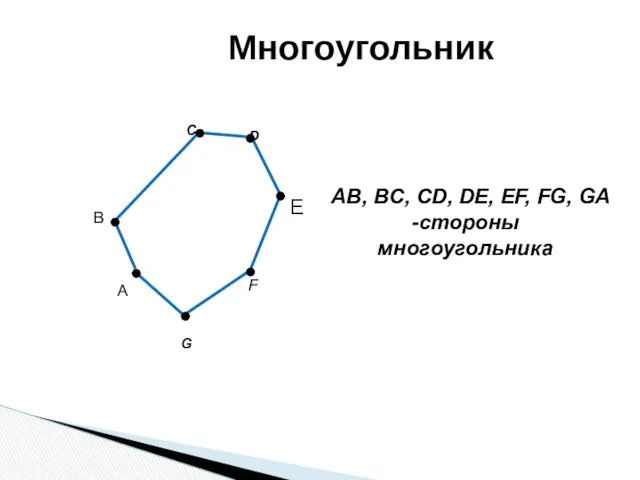
- 7. C F G B AB, BC, CD, DE, EF, FG, GA -стороны многоугольника D Многоугольник E
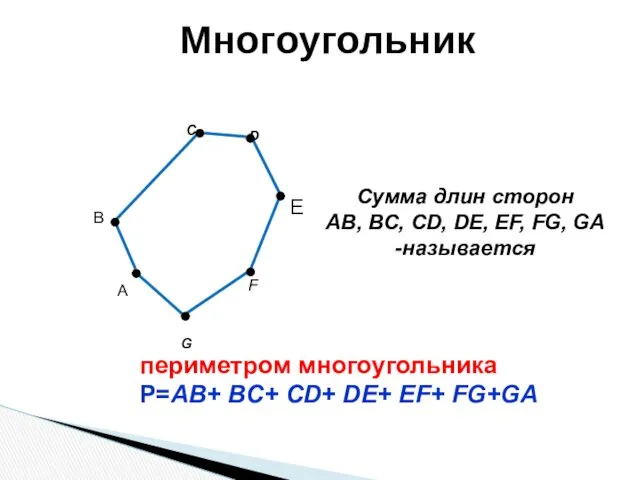
- 8. C F G B Сумма длин сторон AB, BC, CD, DE, EF, FG, GA -называется D
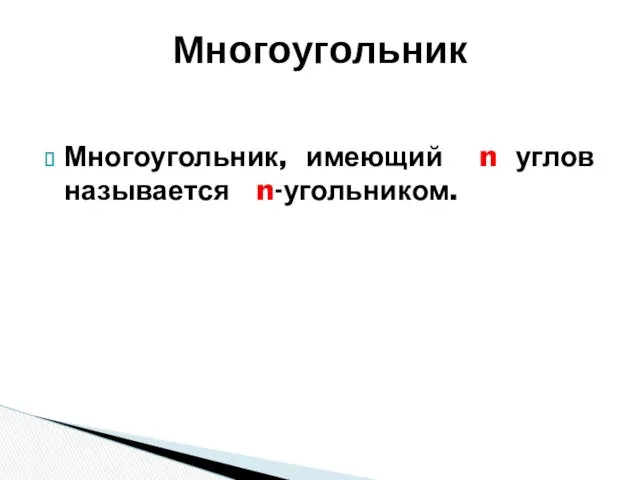
- 9. Многоугольник, имеющий n углов называется n-угольником. Многоугольник
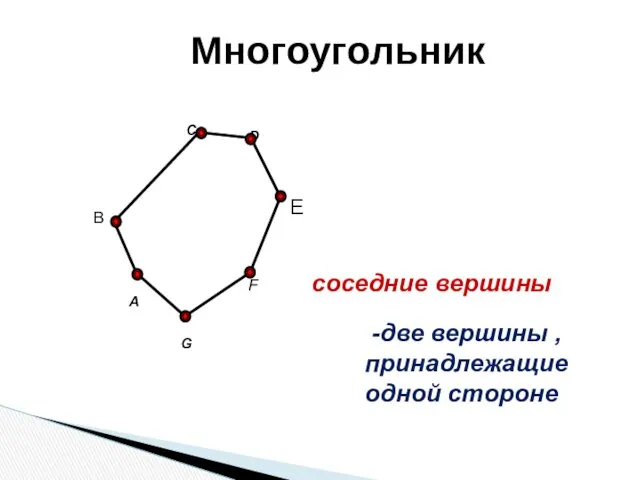
- 10. A C F G B соседние вершины D E -две вершины , принадлежащие одной стороне Многоугольник
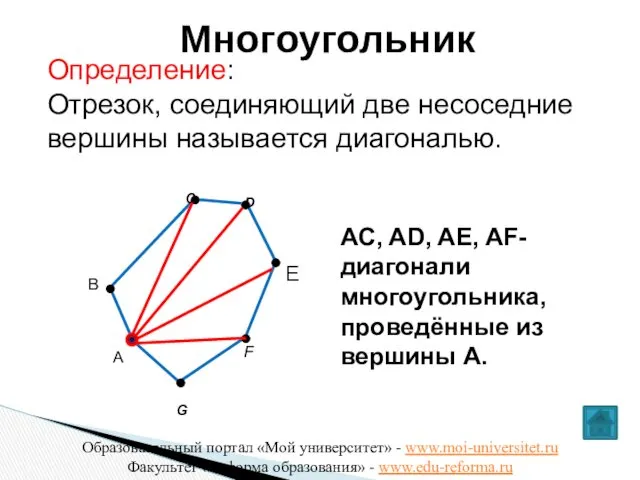
- 11. C F G B D Многоугольник E А AC, AD, AE, AF- диагонали многоугольника, проведённые из
- 12. Выпуклые многоугольники Определение: Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей
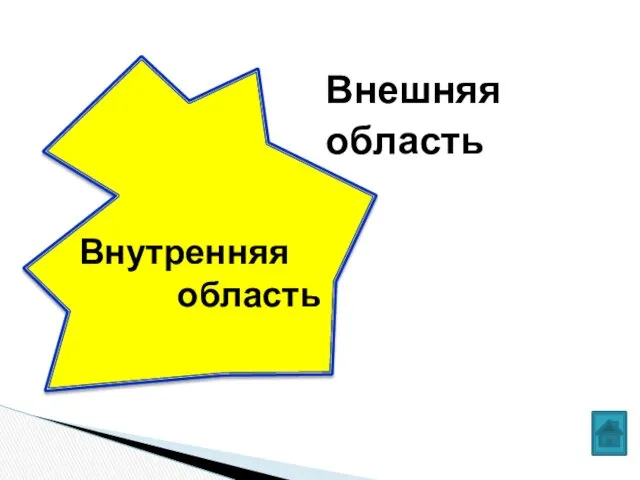
- 13. Внешняя область Внутренняя область
- 14. 30.11.2012 www.konspekturoka.ru Задача Сколько сторон имеет многоугольник, если каждый угол которого равен 120°. Решение Так как
- 15. Четырехугольники Параллелограмм Прямоугольник Ромб Квадрат Трапеция
- 16. Параллелограмм
- 17. Определение Параллелограмм- это четырехугольник, у которого противоположные стороны попарно параллельны. Если в четырехугольнике ABIICD и BCIIAD,
- 18. Свойства параллелограмма 1. В параллелограмме противоположные стороны равны и противоположные углы равны. Если ABCD- параллелограмм, то
- 19. Свойства параллелограмма 2. Диагонали параллелограмма точкой пересечения делятся пополам. Если ABCD- параллелограмм, то AO=OC, BO=OD. В
- 20. Если в задаче дано, что четырехугольник – параллелограмм, то можно использовать свойства параллелограмма.
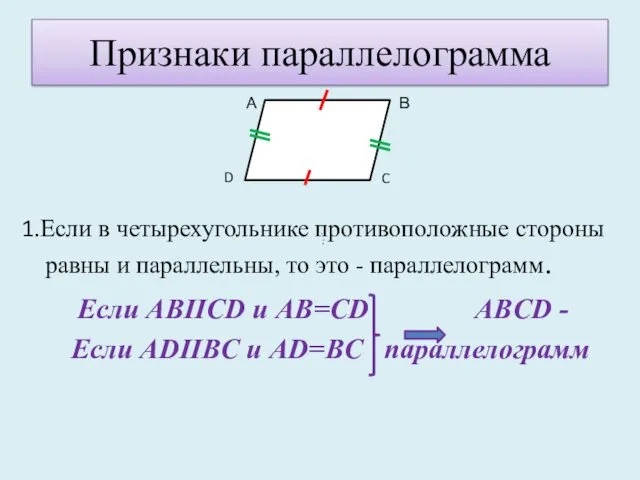
- 21. Признаки параллелограмма 1.Если в четырехугольнике противоположные стороны равны и параллельны, то это - параллелограмм. Если ABIICD
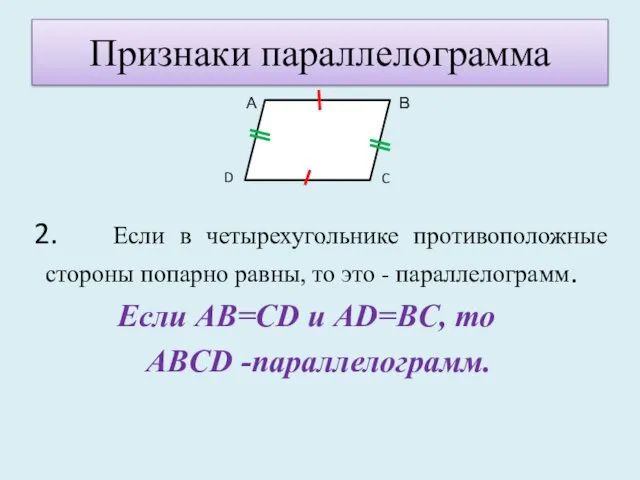
- 22. Признаки параллелограмма 2. Если в четырехугольнике противоположные стороны попарно равны, то это - параллелограмм. Если AB=CD
- 23. Признаки параллелограмма 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то это -
- 24. Если в задаче нужно доказать, что четырехугольник является параллелограммом, то применяют один из признаков параллелограмма.
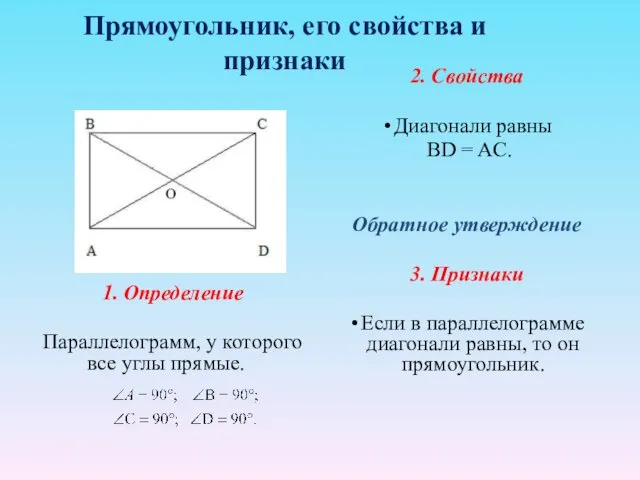
- 25. Прямоугольник, его свойства и признаки 1. Определение Параллелограмм, у которого все углы прямые. 2. Свойства Диагонали
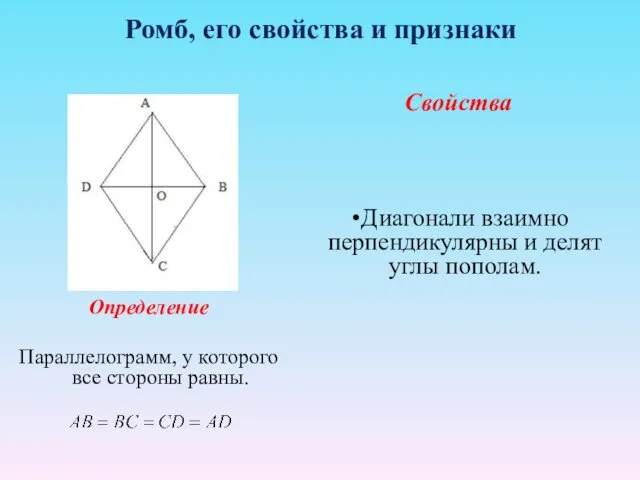
- 26. Ромб, его свойства и признаки Определение Параллелограмм, у которого все стороны равны. Свойства Диагонали взаимно перпендикулярны
- 27. Квадрат, его свойства и признаки Определение Прямоугольник, у которого все стороны равны. Свойства Диагонали равны, взаимно
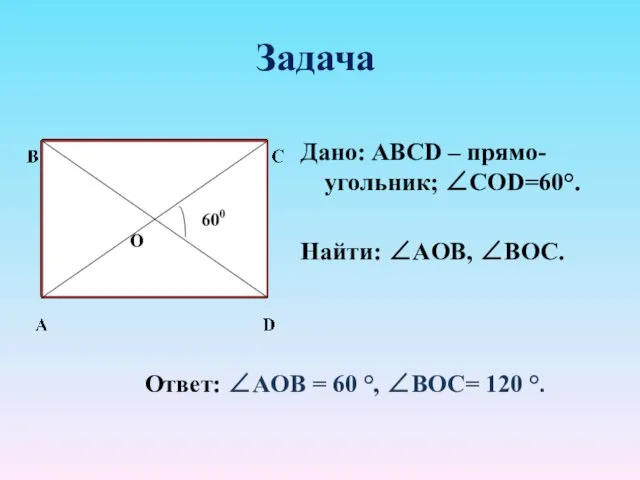
- 28. Задача Дано: ABCD – прямо-угольник; ∠CОD=60°. Найти: ∠АOB, ∠BOC. Ответ: ∠АOB = 60 °, ∠BOC= 120
- 29. Задача Дано: ABCD – прямоугольник; ∠ABD больше ∠СВD на 20°. Найти: углы треугольника АОD. Ответ: ∠А
- 30. Задача В ромбе угол между диагональю и стороной равен 25°. Найдите углы ромба. Ответ: 50°; 130°
- 31. Свойства площадей Равные многоугольники имеют равные площади. Если многоугольник составлен из нескольких многоугольников, то его площадь
- 32. Площадь прямоугольника
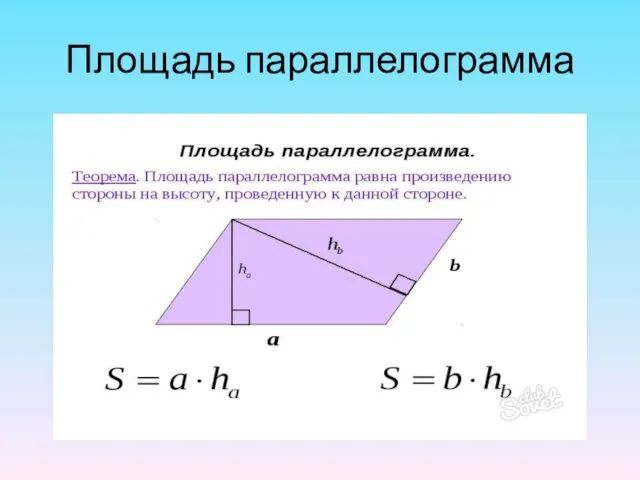
- 33. Площадь параллелограмма
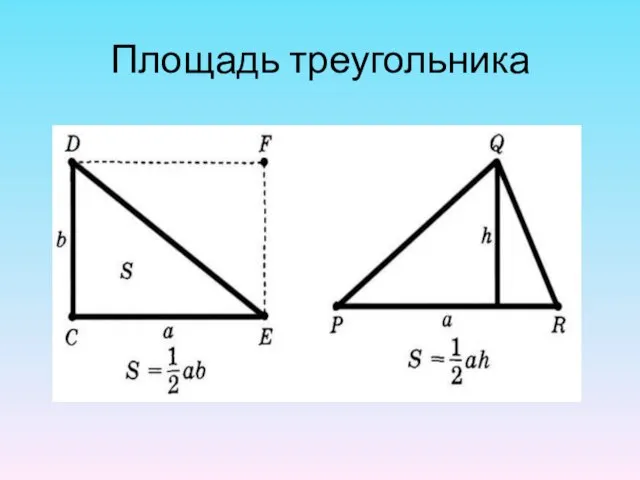
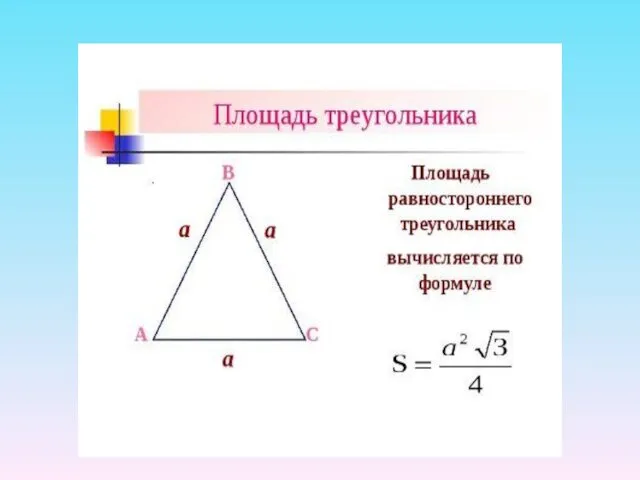
- 34. Площадь треугольника
- 36. Площадь трапеции
- 37. 1. Найти площадь прямоугольника ABCD, если ВС=24, Р=72
- 38. Теорема Пифагора
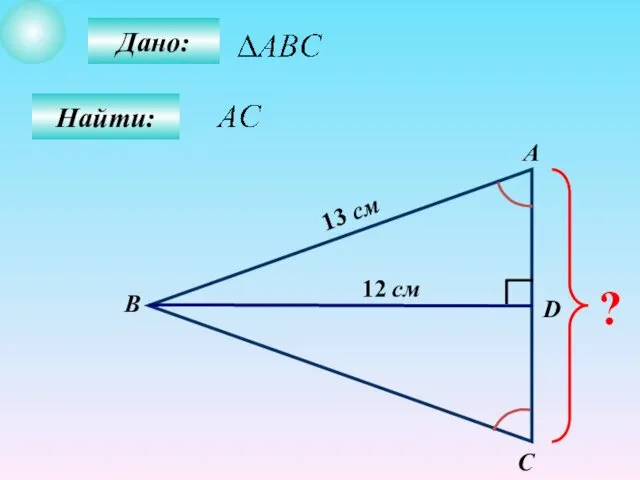
- 39. Дано: Найти: А B C D ? 12 см 13 см
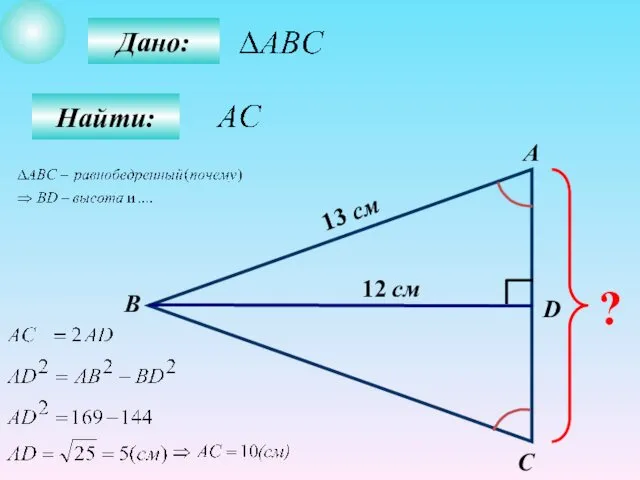
- 40. Дано: Найти: А B C D ? 12 см 13 см
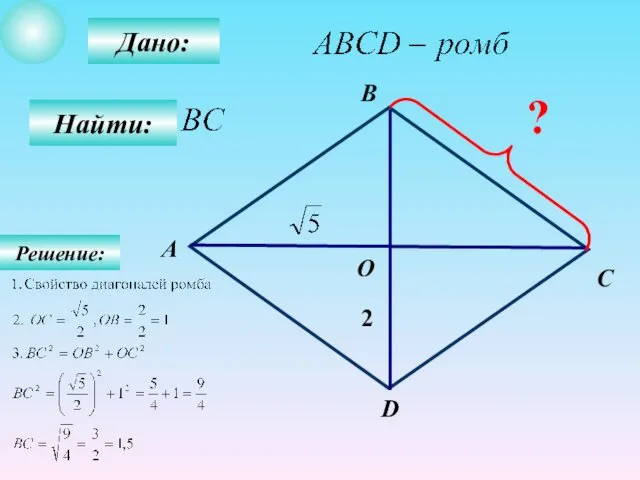
- 41. Дано: Найти: В А С О D 2 ? Решение:
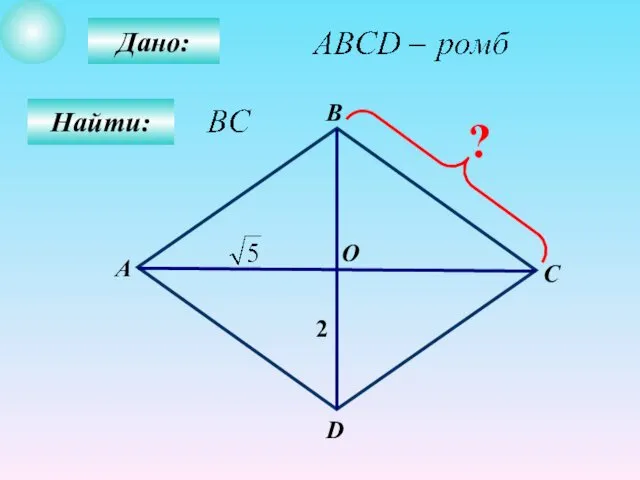
- 42. Дано: Найти: В А С О D 2 ?
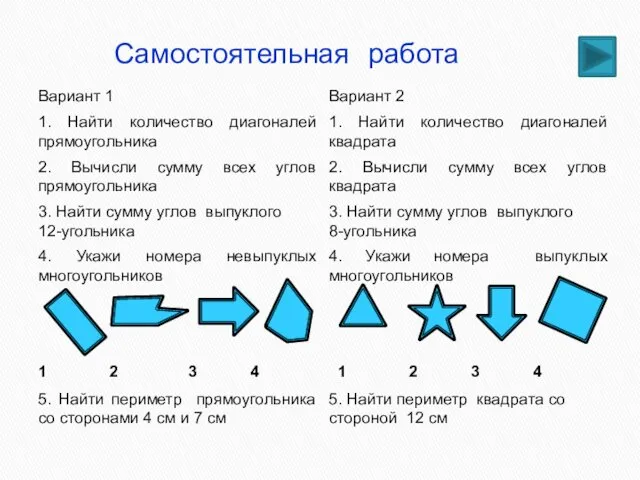
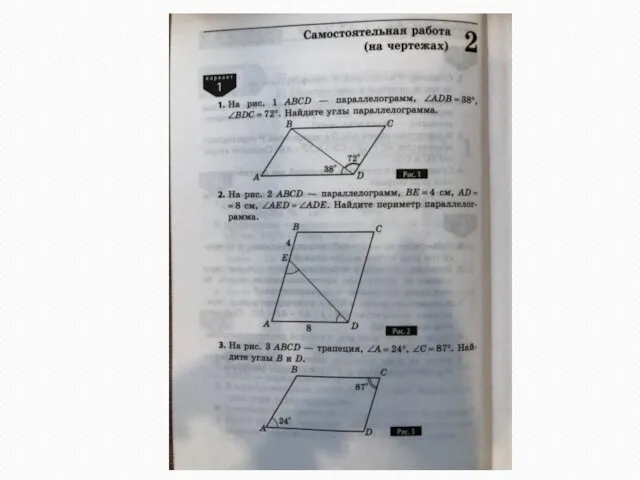
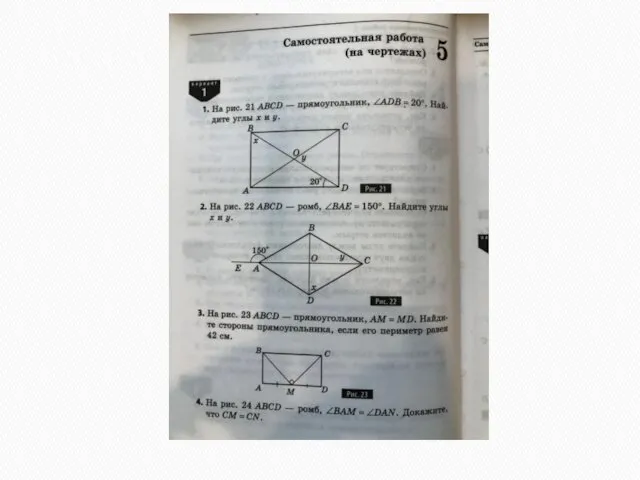
- 43. Самостоятельная работа
- 47. Скачать презентацию





















 презентация таблица сложения с перехдом через десяток
презентация таблица сложения с перехдом через десяток Блез Паскаль (1623-1662 гг.)
Блез Паскаль (1623-1662 гг.) Интересные факты о математике
Интересные факты о математике История возникновения и развития математики
История возникновения и развития математики ЦМР к уроку математики в 1 классе Сложение и вычитание в пределах 10.Закрепление
ЦМР к уроку математики в 1 классе Сложение и вычитание в пределах 10.Закрепление Теорема косинусов
Теорема косинусов Параллель, қиылысатын және айқас түзулер
Параллель, қиылысатын және айқас түзулер Определение окружности, ее основных элементов
Определение окружности, ее основных элементов Вписанные и центральные углы
Вписанные и центральные углы Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения.
Презентация к открытому уроку по математике для 1 класса по теме:Секрет сложения. Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Величины. Длина. (1 класс)
Величины. Длина. (1 класс) Урок математики в 3 классе. По теме: Площадь фигур. Симметричные фигуры. Таблица умножения на 8 и 9.
Урок математики в 3 классе. По теме: Площадь фигур. Симметричные фигуры. Таблица умножения на 8 и 9. Открытый урок математики в 1 классе по теме Табличное сложение +2,+3,+4 (презентация и план-конспект).
Открытый урок математики в 1 классе по теме Табличное сложение +2,+3,+4 (презентация и план-конспект). Стандартный вид числа. Число n
Стандартный вид числа. Число n Математика. Мы с логикой на ТЫ!
Математика. Мы с логикой на ТЫ! Формулы приведения
Формулы приведения ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО.СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДВУХЗНАЧНЫХ ЧИСЕЛ.
ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО.СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДВУХЗНАЧНЫХ ЧИСЕЛ. Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Внеклассное занятие по математике 2 класс Путешествие в Простоквашино. Поиск клада
Внеклассное занятие по математике 2 класс Путешествие в Простоквашино. Поиск клада Урок математики для 2 класса Трёхзначные числа
Урок математики для 2 класса Трёхзначные числа Производная. Решение прикладных задач
Производная. Решение прикладных задач Метод подбора параметра. Экономические задачи
Метод подбора параметра. Экономические задачи Действия с обыкновенными дробями. Умножение и деление
Действия с обыкновенными дробями. Умножение и деление Геометрик фигуралар
Геометрик фигуралар Применение интеграла к решению задач
Применение интеграла к решению задач Презентация сказки Треугольник и Квадрат
Презентация сказки Треугольник и Квадрат Нахождение двух чисел по их сумме и разности
Нахождение двух чисел по их сумме и разности