Содержание
- 2. основным объектом внимания является веро-ятность числа наступлений события А. Пусть P(A) = p. Вероятность того, что
- 3. Формула Бернулли является точной формулой и может применяться при любых n, но, как правило, применяется при
- 4. n = 7 P7,2=C • p2 q7-2 = 2 7 a) m = 2 b) m
- 5. = 0.02799 + 0.13064 + 0.26127 = 0.4199 Наивероятнейшее число наступлений события Пусть проводятся n независимых
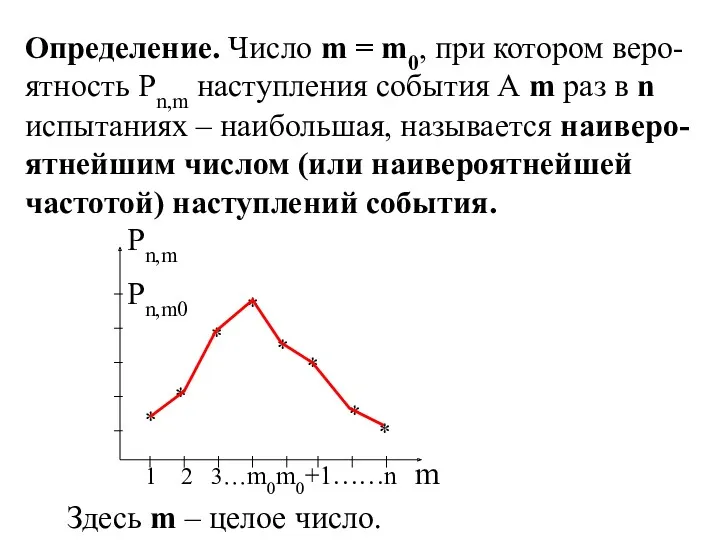
- 6. Определение. Число m = m0, при котором веро-ятность Pn,m наступления события А m раз в n
- 7. np – q ≤ m0 ≤ np+p В этой формуле (np + p) – (np –
- 8. Например: Если 16,4 ≤ m0 ≤ 17,4, то m0 =17. Если 13 ≤ m0 ≤ 14,
- 9. Pn,m0 = C • p2 • q8-2= * 2 8 0.32• 0.76 = 0.296. Локальная теорема
- 10. Здесь Отсюда Свойства малой функции Лапласа φ(x). 1). Функция φ(x) – четна: φ (-x) = φ
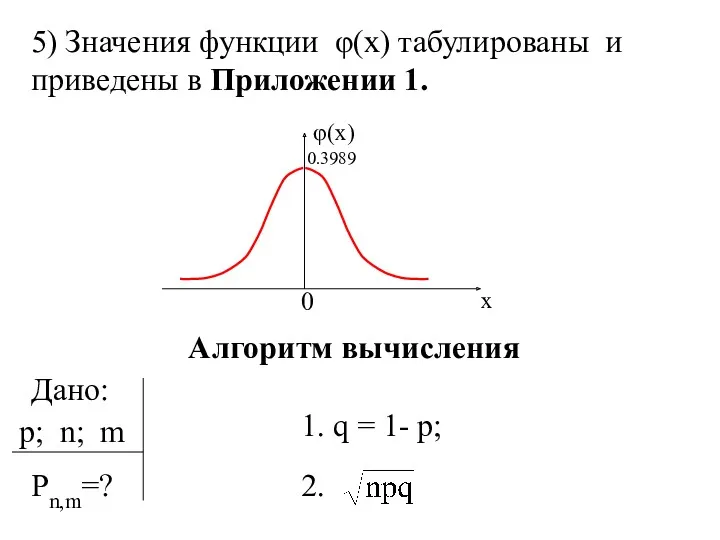
- 11. 5) Значения функции φ(x) табулированы и приведены в Приложении 1. 0 x φ(x) 0.3989 Алгоритм вычисления
- 12. 4. φ(x) – по таблице; 5. Задача. Вероятность того, что посаженное де-рево приживется, равна 0.8. Посажено
- 13. Дано: p = 0.8 n = 100 Pn,m=0.01087 m =? q = 1 – 0.8 =
- 14. x = m – 80 = 2.1*4 = 8.4. m = 80 + 8.4 = 88.
- 15. приближенно равна: P(a ≤ m ≤ b) ≈ ( Φ(β) - Φ(α) ), где Функция Лапласа
- 16. Φ(x) приведены в таблице Приложения 2. Свойства функции Лапласа Φ(x). 1). Φ(x) – нечетна: Φ(- x)
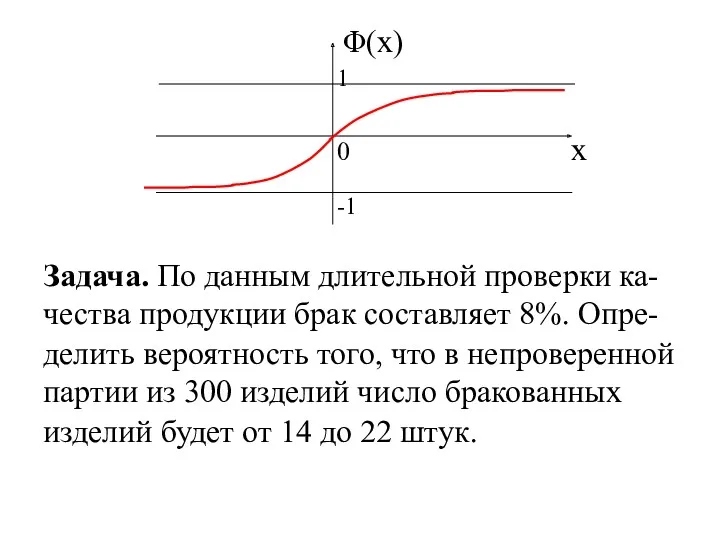
- 17. x Φ(x) 0 Задача. По данным длительной проверки ка-чества продукции брак составляет 8%. Опре- делить вероятность
- 18. Дано: p = 0.08 n = 300 a =14, b =22 P(a ≤ m ≤ b)=?
- 19. = ( - 0.3328 + 0.9668) = 0.317. Следствие из интегральной теоремы Лапласа Теорема. С вероятностью,
- 20. P(│ │≤ ε ) ≈ ≈ Φ(β) Здесь β = Задача. Вероятность того, что покупателю необ-ходима
- 22. Скачать презентацию


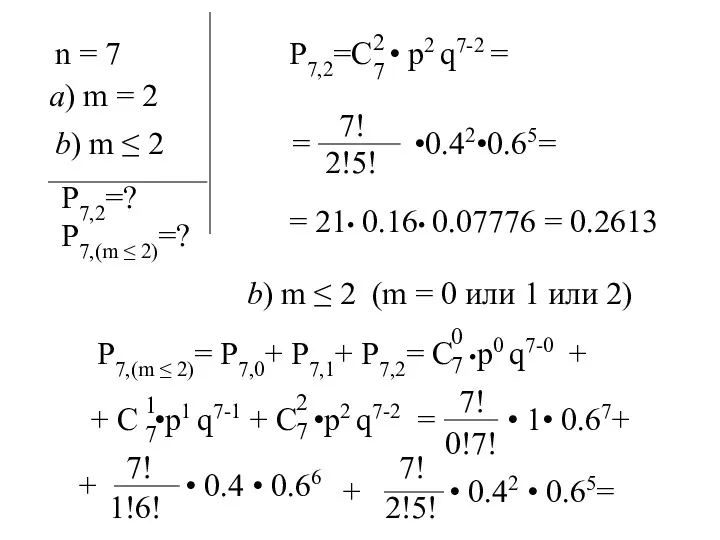










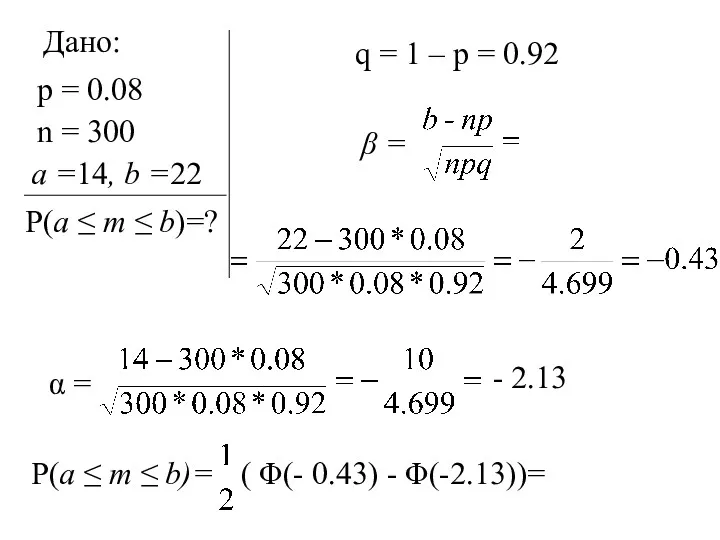


 Повторение. Алгебра 9 класс
Повторение. Алгебра 9 класс Сфера и её элементы. Уравнение сферы в заданной системе координат
Сфера и её элементы. Уравнение сферы в заданной системе координат Задача 3. Определение оптимальных размеров здания по минимуму теплопотерь
Задача 3. Определение оптимальных размеров здания по минимуму теплопотерь Составные задачи 2 класс
Составные задачи 2 класс Методы и алгоритмы цифровой обработки сигналов на базе MATLAB. Адаптивные фильтры
Методы и алгоритмы цифровой обработки сигналов на базе MATLAB. Адаптивные фильтры Тела вращения
Тела вращения Алгоритм решения неравенств методом интервалов
Алгоритм решения неравенств методом интервалов Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Задачи на проценты
Задачи на проценты Имитационные модели
Имитационные модели теория вероятностей в зад ЕГЭ
теория вероятностей в зад ЕГЭ Найти параметр в уравнении
Найти параметр в уравнении Подобие в геометрии. Подобные треугольники
Подобие в геометрии. Подобные треугольники Умножение и деление десятичной дроби на разрядную единицу
Умножение и деление десятичной дроби на разрядную единицу Общее уравнение кривой второго порядка. Аналитическая геометрия
Общее уравнение кривой второго порядка. Аналитическая геометрия Простейшие задачи в координатах
Простейшие задачи в координатах Векторы в пространстве
Векторы в пространстве Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Наглядное представление статистической информации
Наглядное представление статистической информации Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м
Обучение детей измерению с помощью общепринятыхединиц измерения: см, дм, м Решение примеров
Решение примеров Викторина по математике для 6 класса (итоги года)
Викторина по математике для 6 класса (итоги года) Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте
Использование игр-головоломок для развития самостоятельности в выборе способов решения в старшем дошкольном возрасте Игровые задания по обучению решения задач на вычетание
Игровые задания по обучению решения задач на вычетание Математические предложения
Математические предложения Параллельные прямые, перпендикулярные плоскости
Параллельные прямые, перпендикулярные плоскости Дидактические игры в процессе формирования сенсорных эталонов у детей 2-3 лет
Дидактические игры в процессе формирования сенсорных эталонов у детей 2-3 лет Счастливый случай. Игра
Счастливый случай. Игра