Содержание
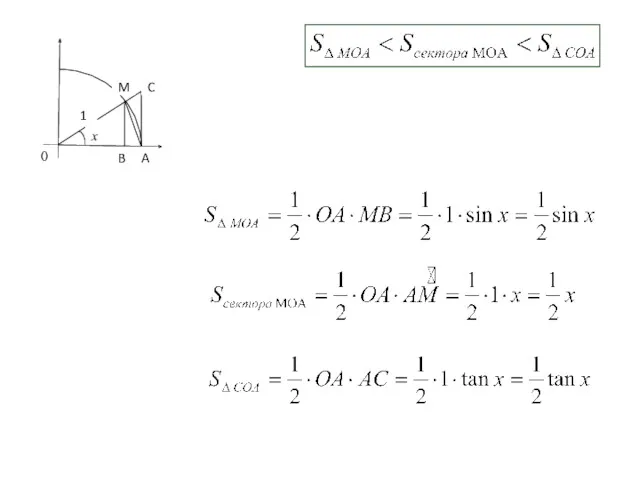
- 2. Замечательные пределы. Доказательство: I. Первый замечательный предел C M A B 1 x 0 Обозначим
- 3. C M A B 1 x 0
- 4. C M A B 1 x 0
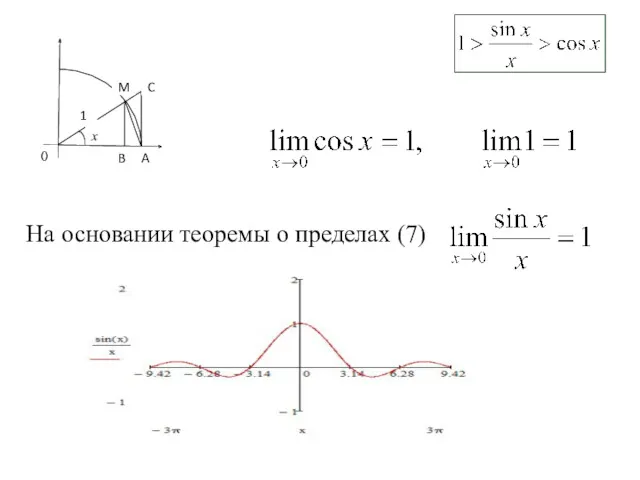
- 5. C M A B 1 x 0 На основании теоремы о пределах (7)
- 6. Вычисление пределов функций Вычислить
- 7. Вычисление пределов функций 2) Вычислить
- 8. II. Второй замечательный предел Теорема 1. Переменная величина при n→∞ имеет предел, заключенный между 2 и
- 9. Определение. Предел переменной величины при n→∞ называется числом е: Из теоремы 1 и определения следует, что
- 10. Теорема 2. Функция при х→∞ имеет предел, равный числу е.
- 11. Доказательство: 1) пусть х→+∞
- 12. Если х→∞ , то и n→∞.
- 13. На основании теоремы о пределах (7): 2) пусть х→-∞. Введем При t→+∞ ,будет х→-∞.
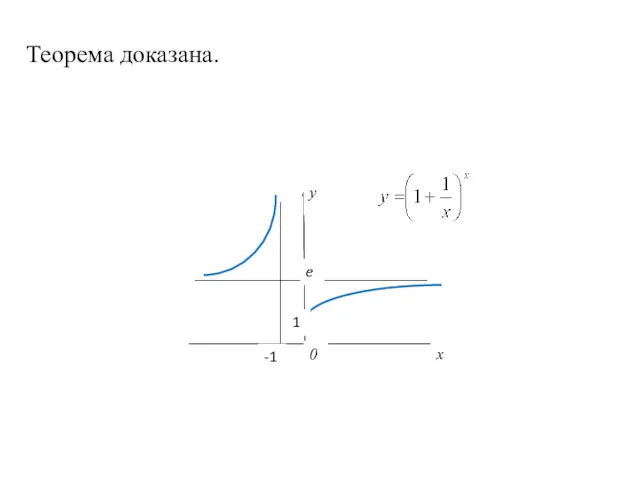
- 14. Теорема доказана. 1 e -1 0 y x
- 15. Если , то при х→∞ имеем α→0 . Тогда
- 16. Вычисление пределов функций Вычислить
- 17. Вычисление пределов функций Вычислить пусть х=2t, тогда
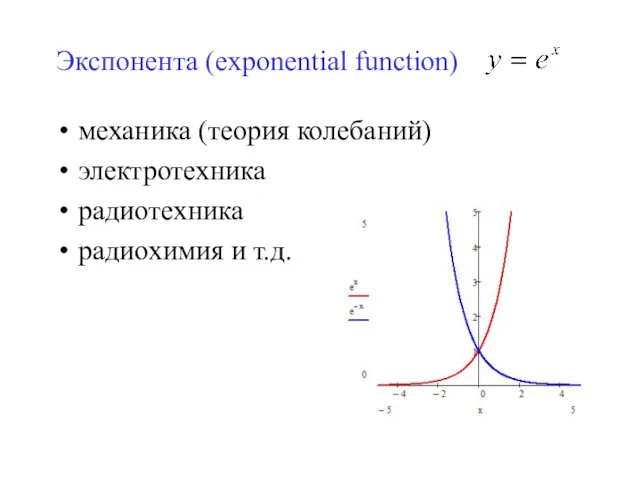
- 18. Экспонента (exponential function) механика (теория колебаний) электротехника радиотехника радиохимия и т.д.
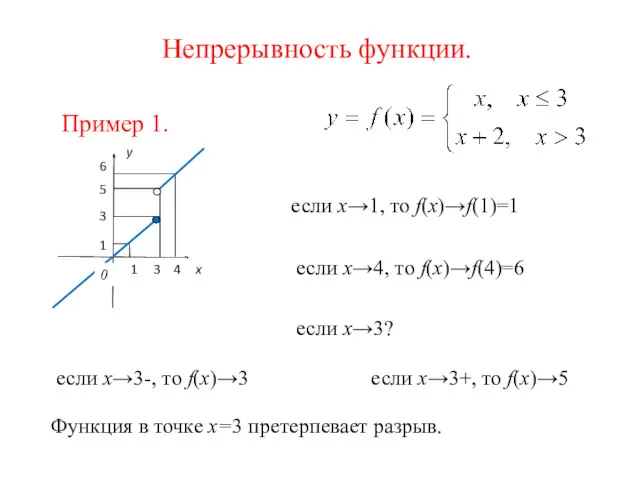
- 19. Непрерывность функции. Пример 1. если х→1, то f(x)→f(1)=1 если х→4, то f(x)→f(4)=6 если х→3? если х→3-,
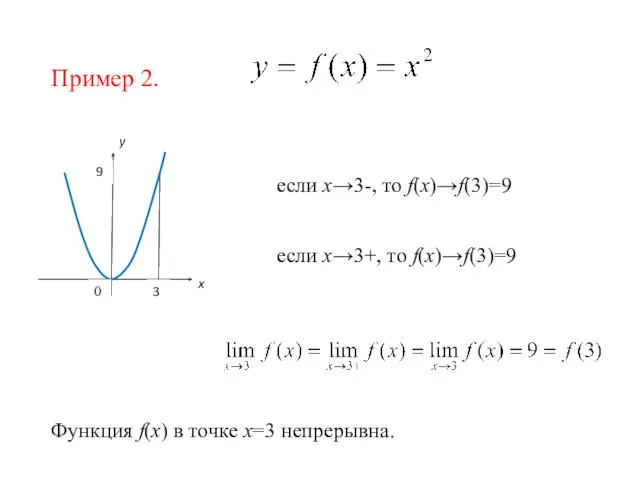
- 20. Пример 2. если х→3-, то f(x)→f(3)=9 Функция f(x) в точке х=3 непрерывна. если х→3+, то f(x)→f(3)=9
- 21. Определение 1. Функция f(x) называется непрерывной в точке х0, если (функция непрерывна в точке х0, если
- 22. Исследовать данную функцию на непрерывность Для х1=0: Функция f(x) в точке х1=0 имеет разрыв.
- 23. т.е. Для х2=2: Функция f(x) в точке х2=2 непрерывна.
- 24. 1 2 0 y x
- 25. так как , то Если функция непрерывна, то при отыскании её предела можно вместо аргумента подставить
- 26. Вычислить предел функции:
- 27. Определение 2. Функция f(x) называется непрерывной, если бесконечно малому приращению аргумента отвечает бесконечно малое же приращение
- 28. Сравнение бесконечно малых. Пусть при х→х0 функции α(х)→0 и β(х)→0. Тогда: 1) если , то α(х)
- 29. пример. Пусть α(х) есть бесконечно малая более высокого порядка, чем β(х).
- 30. если , то α(х) и β(х) называются бесконечно малыми одного порядка . Пример. Функции sin3x и
- 31. если , то α(х) и β(х) называются эквивалентными бесконечно малыми. (α(х)∽ β(х)) Пример. Функции sinx и
- 32. Пример. Функции ln(1+x) и x являются при х→0 эквивалентными бесконечно малыми (ln(1+x)∽x) , т.к.
- 33. если , то α(х) называется бесконечно малой n-го порядка относительно β(х) Пример. Функция 1-cosx является при
- 34. Для бесконечно больших функций имеют место аналогичные правила сравнения. Пример. Функция является при х→∞ бесконечно большой
- 35. Примеры эквивалентных бесконечно малых функций:. sin x ~ x arctan x ~ x arcsin x ~
- 37. Скачать презентацию

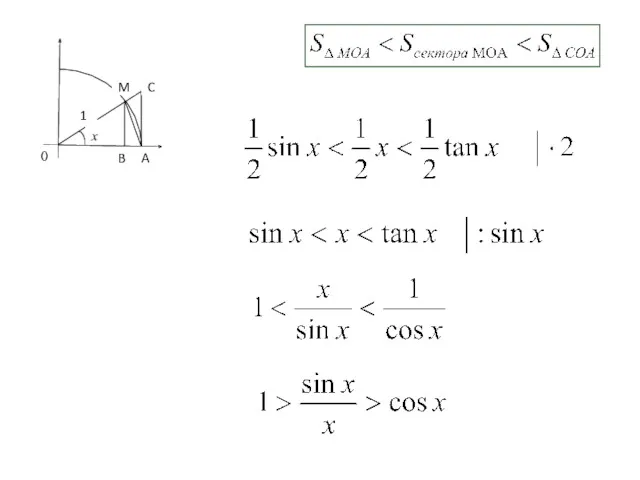






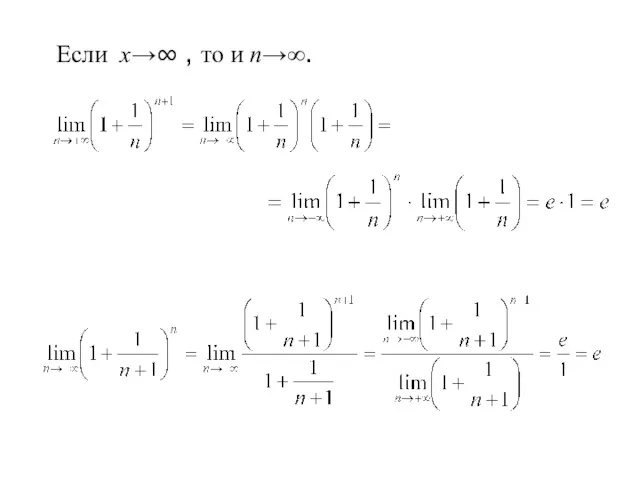







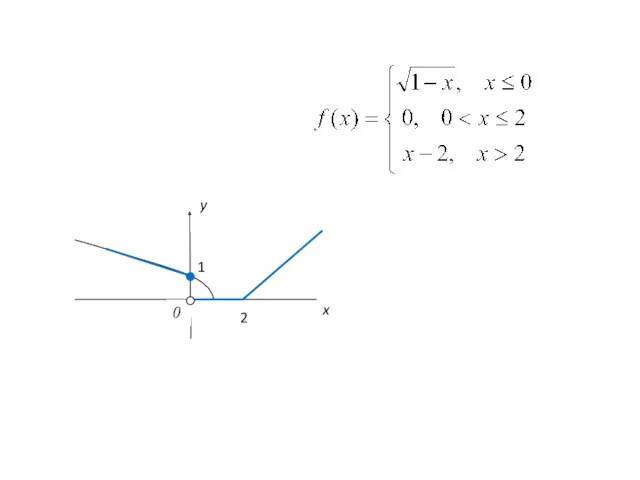











 Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов Знакомство с новой единицей измерения длины. Дециметр
Знакомство с новой единицей измерения длины. Дециметр Урок 1. Таблица сложения однозначных чисел
Урок 1. Таблица сложения однозначных чисел Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений Cложение и вычитание чисел с разными знаками. Обобщающий урок. 6 класс
Cложение и вычитание чисел с разными знаками. Обобщающий урок. 6 класс Состав числа 10
Состав числа 10 Знаки < или >
Знаки < или > Эконометрика: Постановка задачи
Эконометрика: Постановка задачи Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Теорема Пифагора
Теорема Пифагора Внешний угол треугольника. Задания для устного счета. Упражнение 10. 7 класс
Внешний угол треугольника. Задания для устного счета. Упражнение 10. 7 класс Геометрическое место точек
Геометрическое место точек Парная регрессия и корреляция. Статистическая зависимость (независимость) случайных переменных
Парная регрессия и корреляция. Статистическая зависимость (независимость) случайных переменных Стандартный вид числа
Стандартный вид числа Открытый урок Числа от 0 до 10 Диск
Открытый урок Числа от 0 до 10 Диск Измерение отрезков
Измерение отрезков Задачи на умножение и деление
Задачи на умножение и деление Умножение натуральных чисел
Умножение натуральных чисел Презентация: Составляем задачи на разностное и кратное сравнение по математике о животных.
Презентация: Составляем задачи на разностное и кратное сравнение по математике о животных. Теоремы. Применение теорем
Теоремы. Применение теорем Приемы вычисления вида 30-7
Приемы вычисления вида 30-7 Множества. Операции над множествами
Множества. Операции над множествами Круговые диаграммы
Круговые диаграммы Производная функции. Возрастание и убывание функций
Производная функции. Возрастание и убывание функций Первообразная функции. Неопределенный интеграл
Первообразная функции. Неопределенный интеграл Количественное описание математических объектов
Количественное описание математических объектов Перетворення подібності. Гомотетія
Перетворення подібності. Гомотетія Приращение аргумента, приращение функции
Приращение аргумента, приращение функции