Содержание
- 2. Понятие числовой последовательности Рассмотрим ряд натуральных чисел N: 1, 2, 3, …, n – 1, n,
- 3. Примеры числовых последовательностей 1, 2, 3, 4, 5, … – ряд натуральных чисел; 2, 4, 6,
- 4. Способы задания последовательностей Перечислением членов последовательности (словесно). Заданием аналитической формулы. Заданием рекуррентной формулы. Примеры: Последовательность простых
- 5. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной сверху, если все ее члены не больше некоторого числа.
- 6. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной снизу, если все ее члены не меньше некоторого числа.
- 7. Возрастание и убывание числовой последовательности Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего:
- 8. Предел числовой последовательности Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении
- 9. Предел числовой последовательности Это определение означает, что a есть предел числовой последовательности, если её общий член
- 10. Рассмотрим последовательность: – гармонический ряд Если │q│ Если │q│> 1, то последовательность уn = q n
- 11. Свойства пределов предел частного равен частному пределов: предел произведения равен произведению пределов: предел суммы равен сумме
- 12. Примеры:
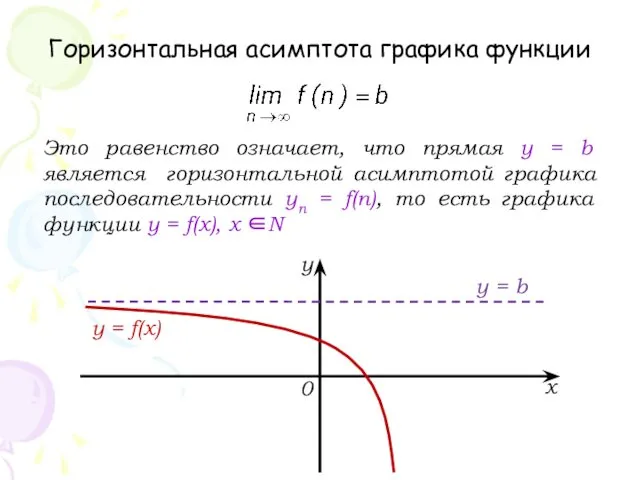
- 13. Это равенство означает, что прямая у = b является горизонтальной асимптотой графика последовательности yn = f(n),
- 14. Предел функции
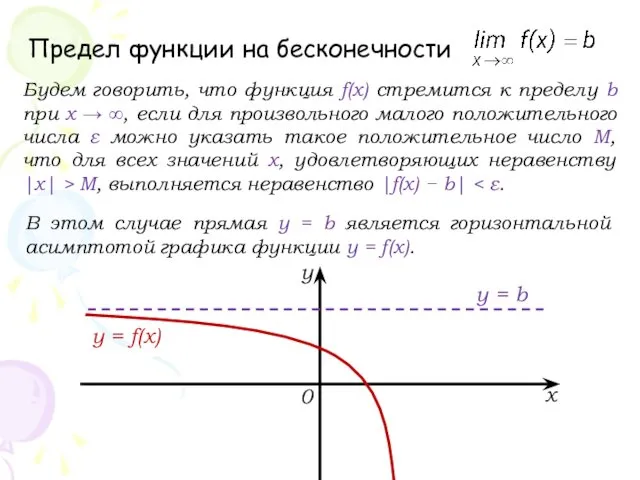
- 15. Предел функции на бесконечности В этом случае прямая у = b является горизонтальной асимптотой графика функции
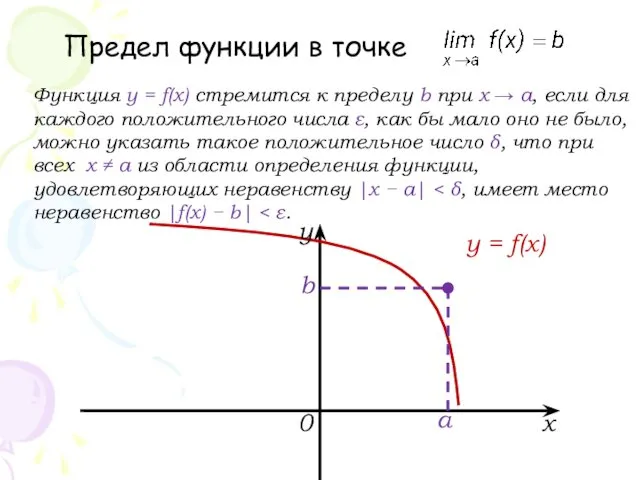
- 16. Предел функции в точке Функция y = f(x) стремится к пределу b при x → a,
- 17. Бесконечно малые и Бесконечно большие
- 18. Функция α(x) называется бесконечно малой величиной при x → a (или при x → ∞), если
- 19. Функция f (x) называется бесконечно большой величиной при x → a (или при x → ∞),
- 20. Таблица эквивалентности Если предел отношения двух бесконечно малых равен единице: то их называют эквивалентными при x
- 21. Теоремы о пределах. Вычисление пределов Первый и второй замечательные пределы
- 22. Рассмотрим теоремы, которые облегчают нахождение пределов функций. Предел суммы (разности) двух функций равен сумме (разности) пределов:
- 23. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: Предел
- 24. Если между соответствующими значениями трех функций при этом: тогда: выполняются неравенства: Если функция f(x) монотонна и
- 25. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 26. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 27. Первый замечательный предел Это означает, что синус малого угла есть бесконечно малая того же порядка, что
- 29. Скачать презентацию























 Квадрат и куб числа
Квадрат и куб числа Правило умножения для комбинаторных задач
Правило умножения для комбинаторных задач Средняя линия треугольника
Средняя линия треугольника Теорема синусов. Теорема косинусов
Теорема синусов. Теорема косинусов презентация по математике Геометрические фигуры для младшей группы
презентация по математике Геометрические фигуры для младшей группы Простые и составные числа
Простые и составные числа Вычитание вида 12 -
Вычитание вида 12 - Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Признаки параллельности двух прямых
Признаки параллельности двух прямых Решение практикоориентированных задач при подготовке к ГИА в 9 классе
Решение практикоориентированных задач при подготовке к ГИА в 9 классе Булевы функции и алгебра логики
Булевы функции и алгебра логики Организация и этапы статистического исследования
Организация и этапы статистического исследования Десятичная запись дробных чисел
Десятичная запись дробных чисел Умножение рациональных чисел
Умножение рациональных чисел Что? Где? Почему? Урок – игра
Что? Где? Почему? Урок – игра Умножение и деление многозначных чисел на однозначное. Закрепление.
Умножение и деление многозначных чисел на однозначное. Закрепление. Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Построение графиков сложных функций на основе свойства монотонности
Построение графиков сложных функций на основе свойства монотонности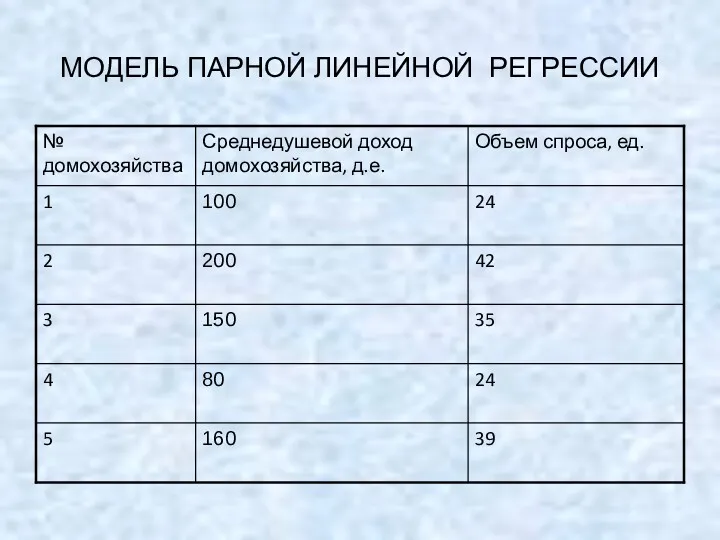 Модель парной линейной регрессии
Модель парной линейной регрессии Тест по теме: Комбинации тел вращения. Вариант 2
Тест по теме: Комбинации тел вращения. Вариант 2 Физико–математический турнир для учащихся 10-11 классов
Физико–математический турнир для учащихся 10-11 классов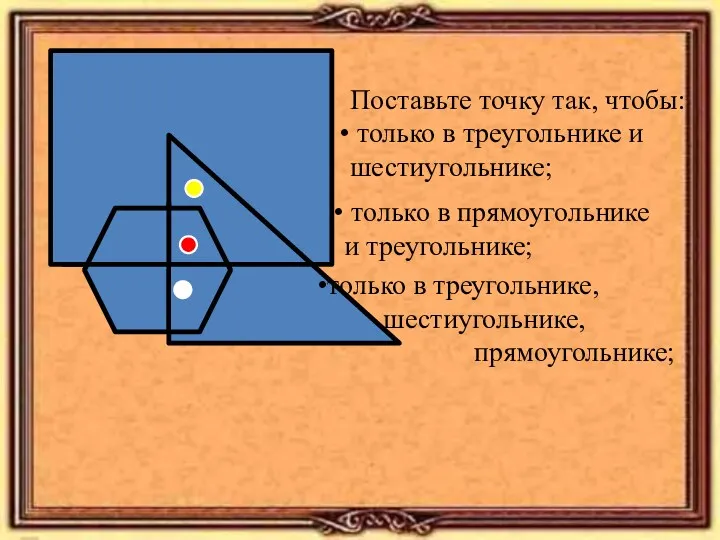 Работа с геометрическими фигурами.
Работа с геометрическими фигурами. Действия с обыкновенными дробями. 6 класс
Действия с обыкновенными дробями. 6 класс Индивидуальная самостоятельная работа Решение задач.
Индивидуальная самостоятельная работа Решение задач. Метод математической индукции
Метод математической индукции Скалярное произведение векторов
Скалярное произведение векторов Игра – тренажёр. Где чей домик? Математика 1 - 2 класс
Игра – тренажёр. Где чей домик? Математика 1 - 2 класс Презентация. Задачи на конкретный смысл умножения
Презентация. Задачи на конкретный смысл умножения