Содержание
- 2. Рассмотрим преобразования графика функции у = f (x) в график функции у = k f (
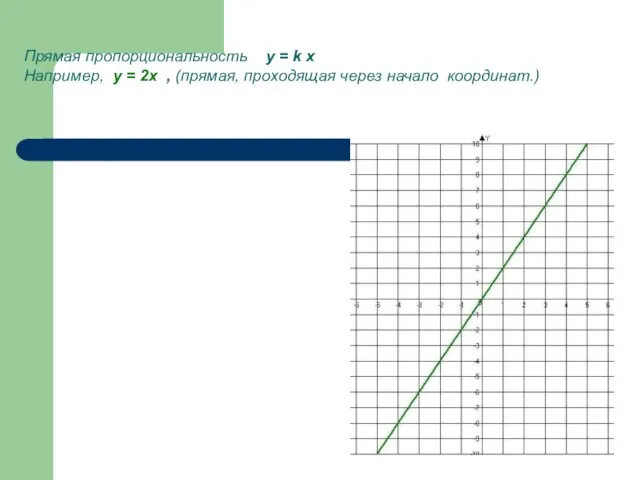
- 3. Прямая пропорциональность y = k x Например, у = 2х , (прямая, проходящая через начало координат.)
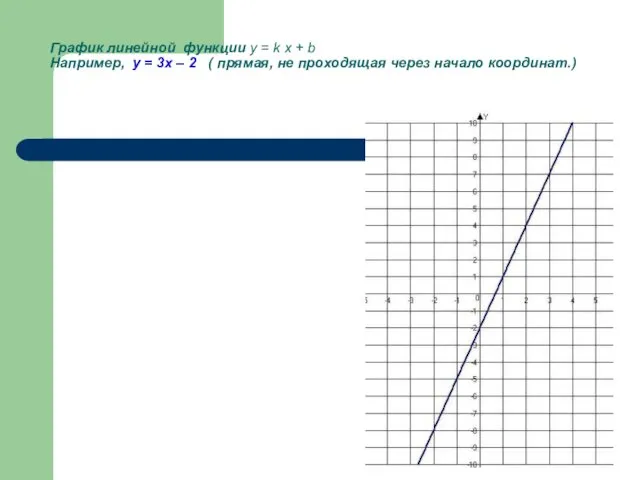
- 4. График линейной функции y = k x + b Например, у = 3х – 2 (
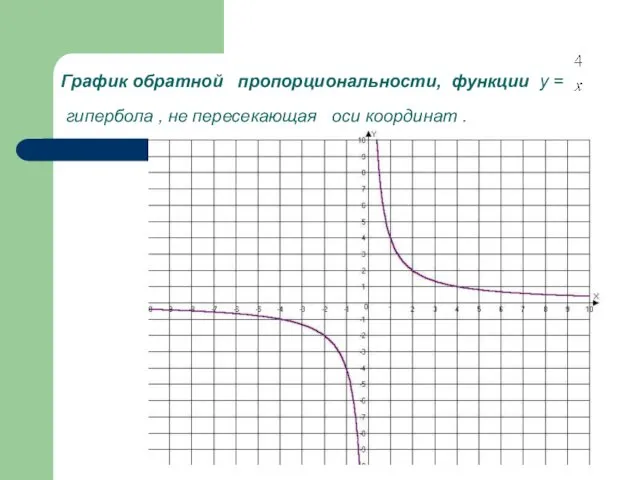
- 5. График обратной пропорциональности, функции у = гипербола , не пересекающая оси координат .
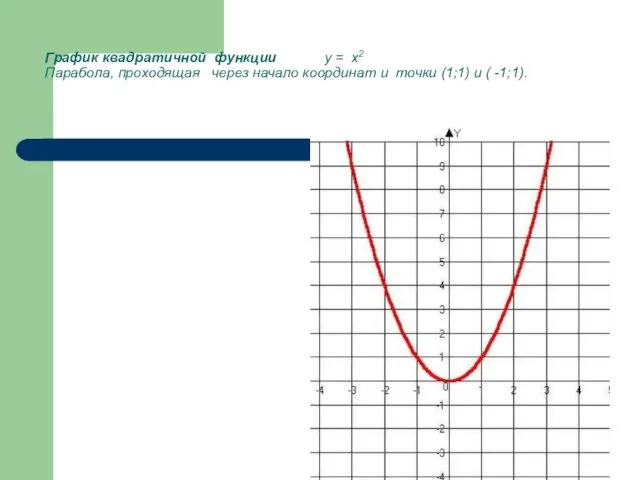
- 6. График квадратичной функции y = x2 Парабола, проходящая через начало координат и точки (1;1) и (
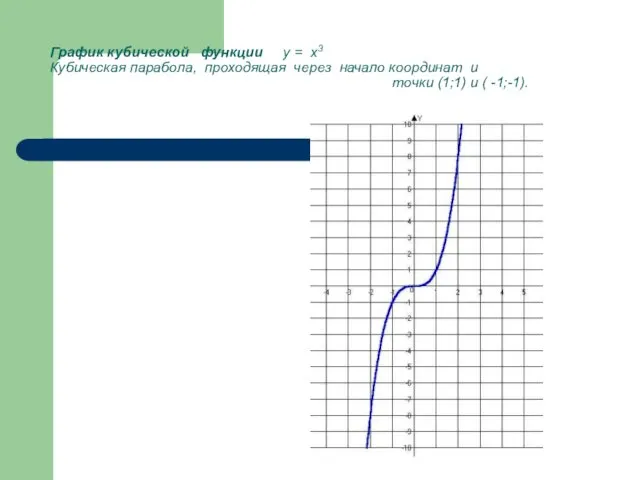
- 7. График кубической функции y = x3 Кубическая парабола, проходящая через начало координат и точки (1;1) и
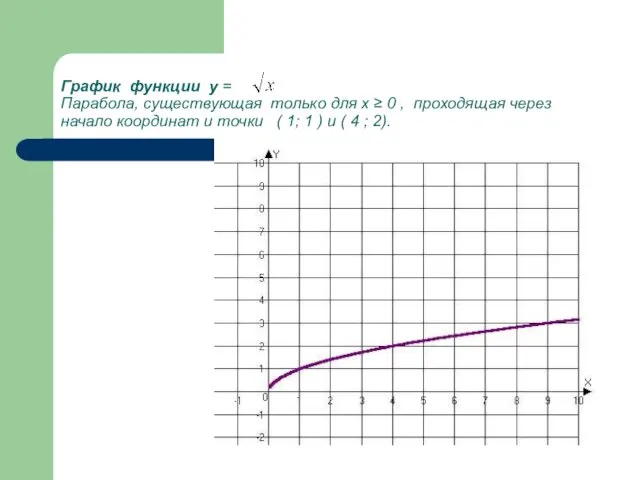
- 8. График функции y = Парабола, существующая только для х ≥ 0 , проходящая через начало координат
- 9. Теперь повторим материал 8 класса по уравнению прямой y = k∙x + b Как проходит прямая
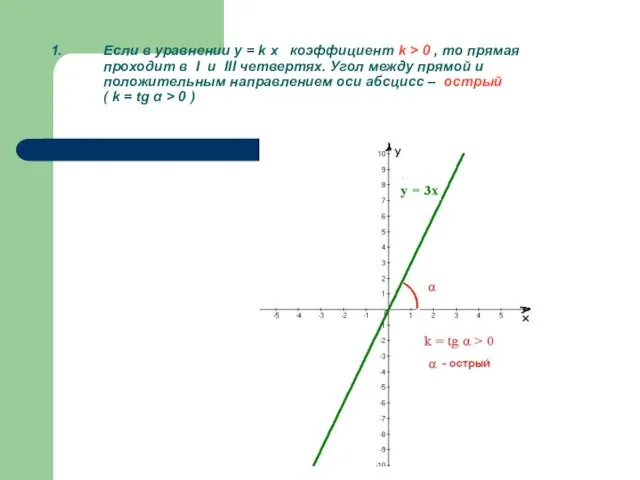
- 10. Если в уравнении y = k x коэффициент k > 0 , то прямая проходит в
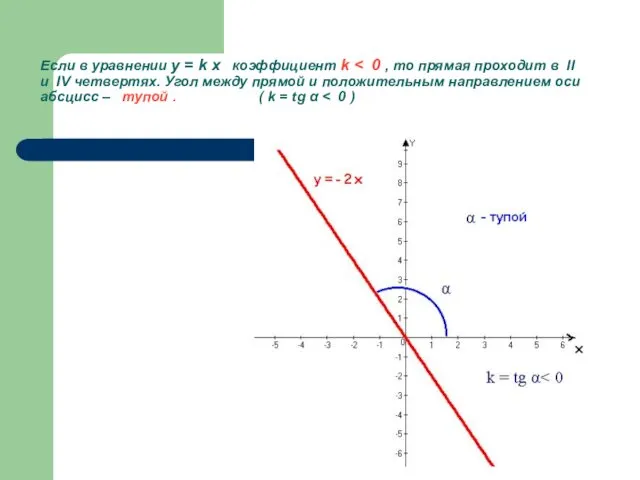
- 11. Если в уравнении y = k x коэффициент k
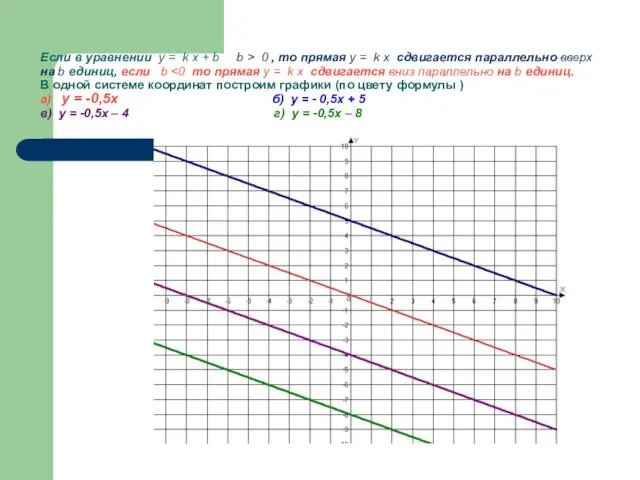
- 12. Если в уравнении y = k x + b b > 0 , то прямая y
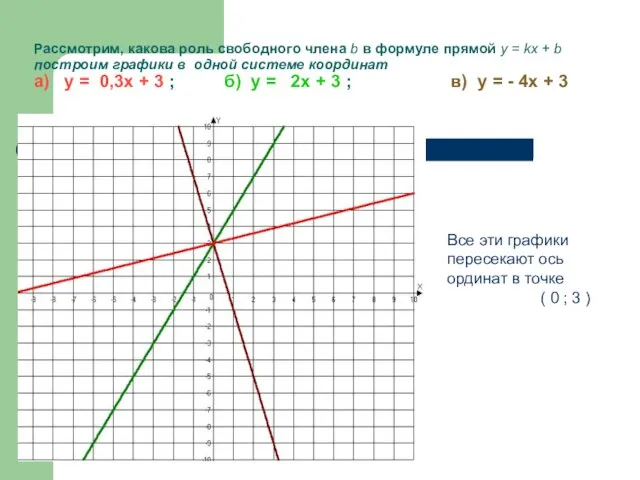
- 13. Рассмотрим, какова роль свободного члена b в формуле прямой у = kx + b построим графики
- 14. Мы всё ближе к осознанию преобразования графика функции у = f (x) в график функции у
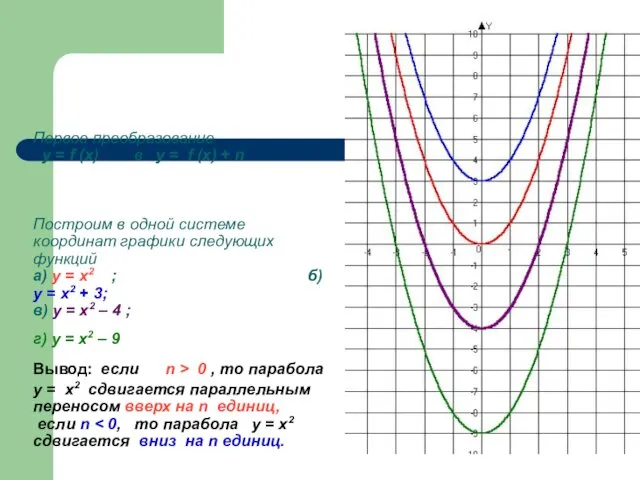
- 15. Первое преобразование у = f (x) в у = f (x) + n Построим в одной
- 16. Рассмотрим преобразование, которое мы не могли наблюдать с графиками прямых. Общий вид преобразования у = f
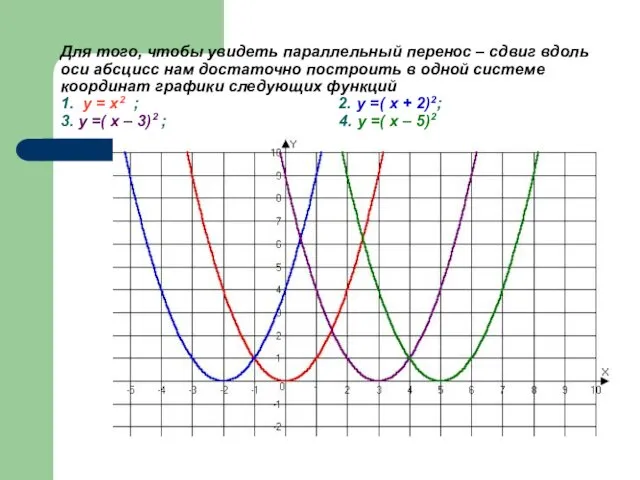
- 17. Для того, чтобы увидеть параллельный перенос – сдвиг вдоль оси абсцисс нам достаточно построить в одной
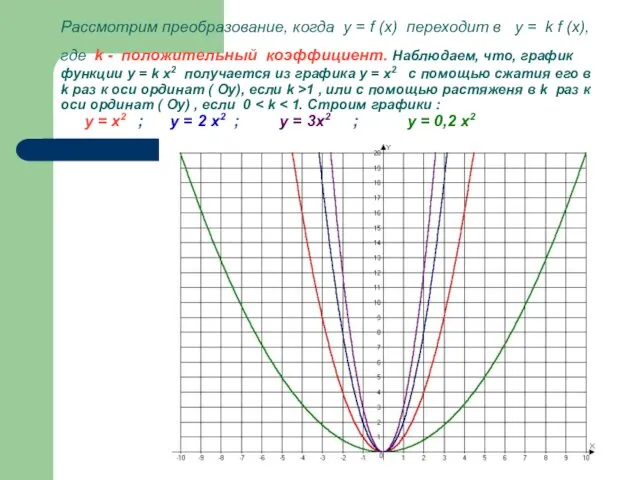
- 18. Теперь рассмотрим преобразование у = f (x) и у = k f (x). Оценим роль коэффициента
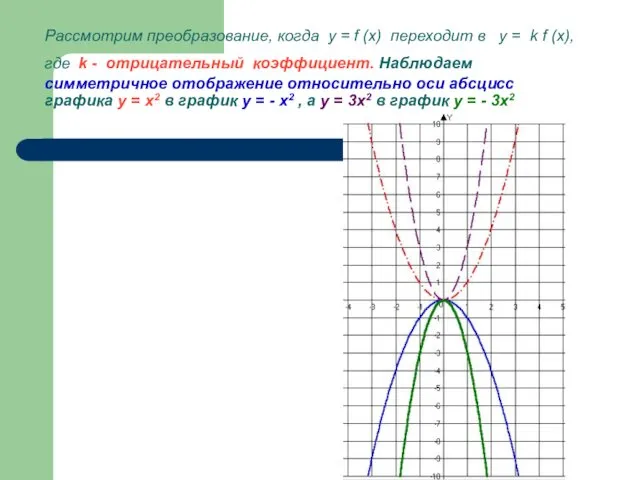
- 19. Рассмотрим преобразование, когда у = f (x) переходит в у = k f (x), где k
- 20. Рассмотрим преобразование, когда у = f (x) переходит в у = k f (x), где k
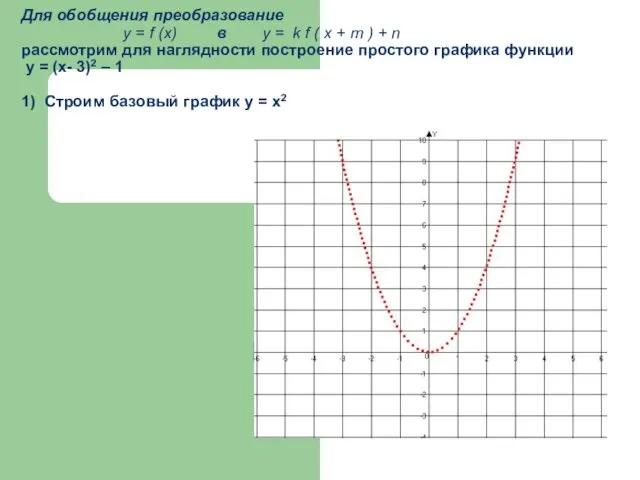
- 21. Для обобщения преобразование у = f (x) в у = k f ( x + m
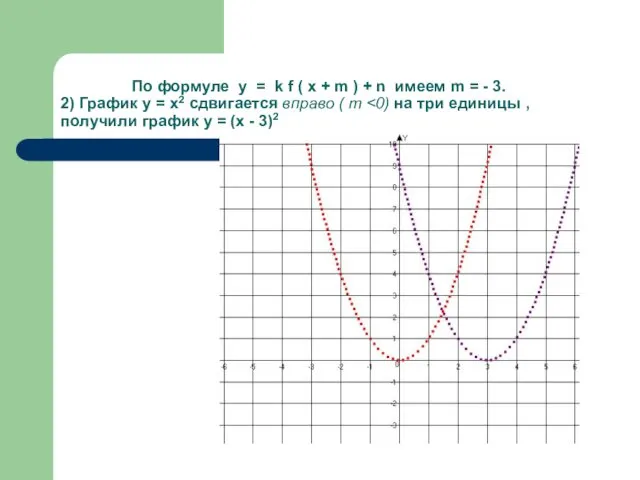
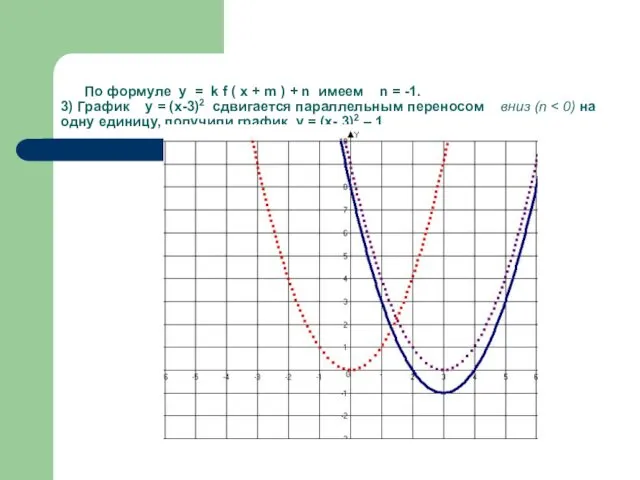
- 22. По формуле у = k f ( x + m ) + n имеем m =
- 23. По формуле у = k f ( x + m ) + n имеем n =
- 24. Подведем итоговое преобразование, комплексно объединяющее все предыдущие преобразования у = f (x) в у = k
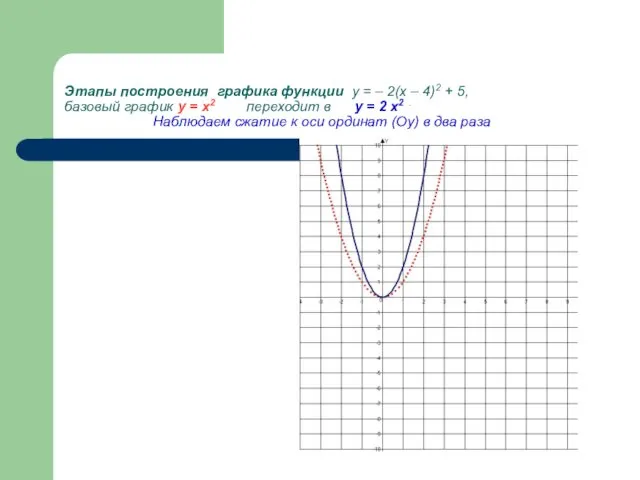
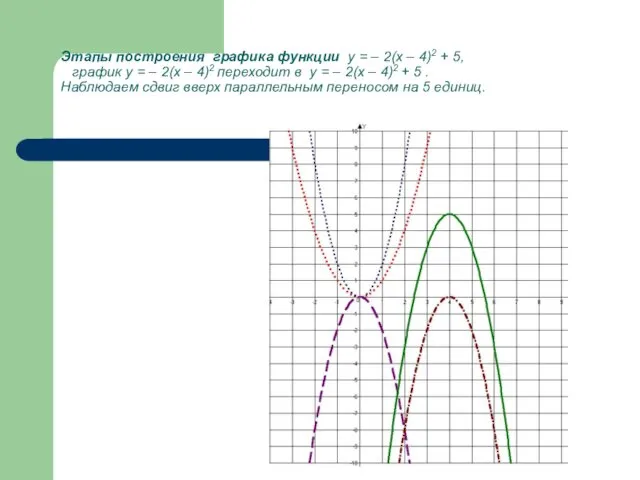
- 25. Этапы построения графика функции у = – 2(х – 4)2 + 5, базовый график у =
- 26. Этапы построения графика функции у = – 2(х – 4)2 + 5, график у = 2х2
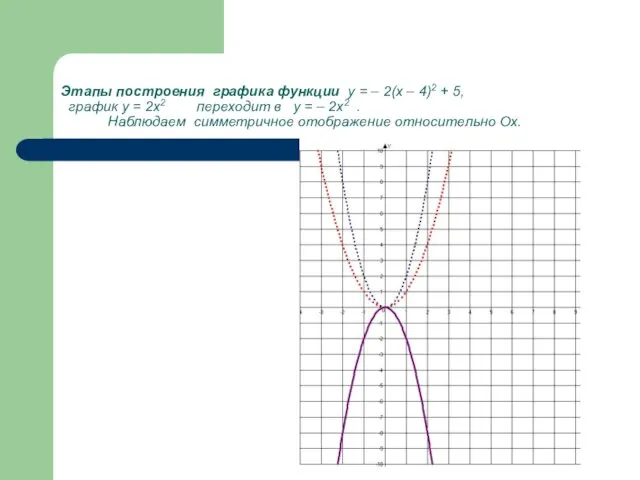
- 27. Этапы построения графика функции у = – 2(х – 4)2 + 5, график у = –
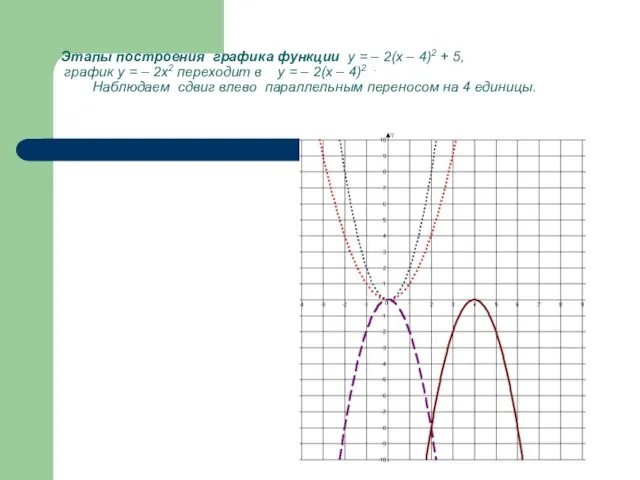
- 28. Этапы построения графика функции у = – 2(х – 4)2 + 5, график у = –
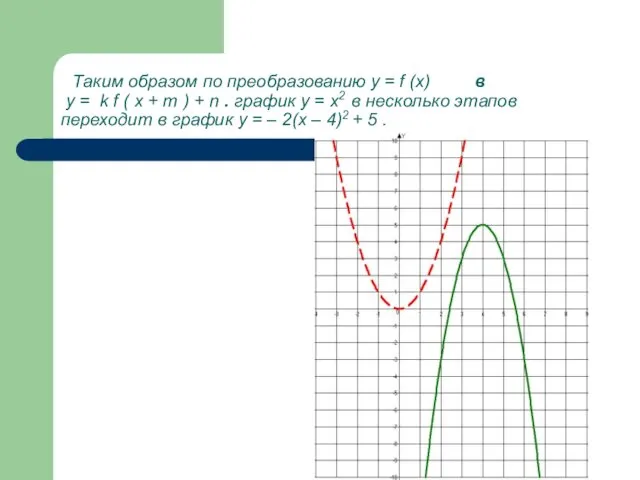
- 29. Таким образом по преобразованию у = f (x) в у = k f ( x +
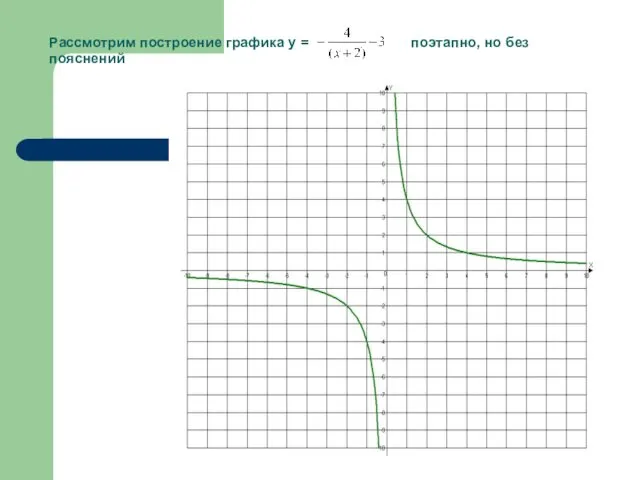
- 30. Рассмотрим построение графика у = поэтапно, но без пояснений
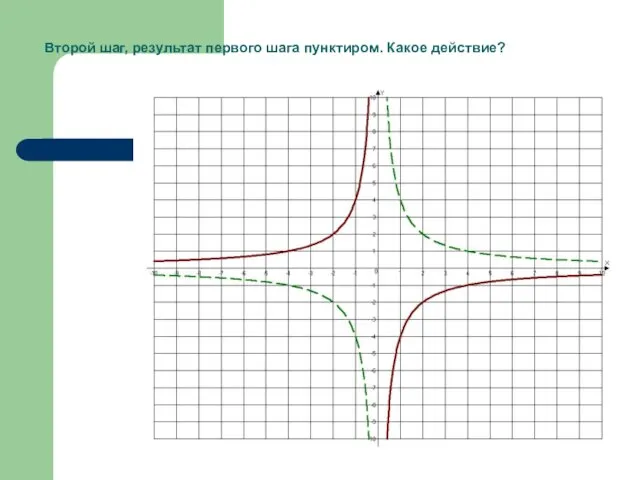
- 31. Второй шаг, результат первого шага пунктиром. Какое действие?
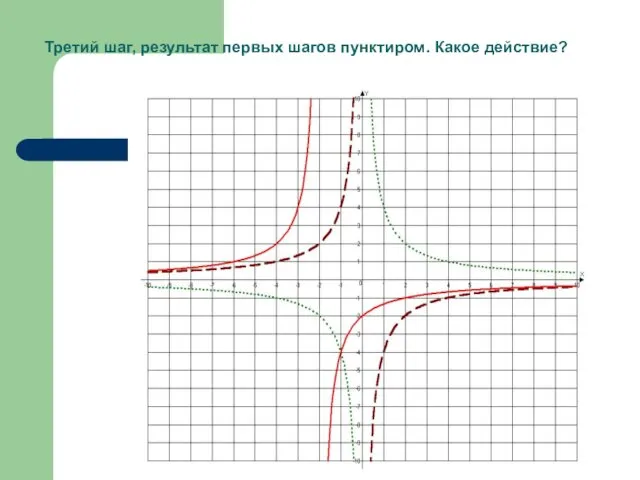
- 32. Третий шаг, результат первых шагов пунктиром. Какое действие?
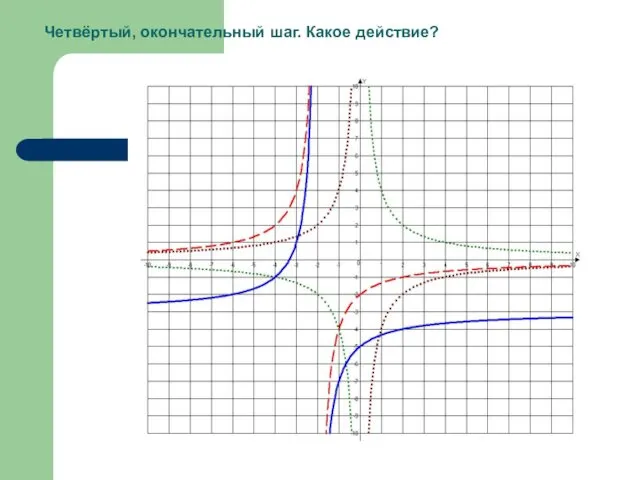
- 33. Четвёртый, окончательный шаг. Какое действие?
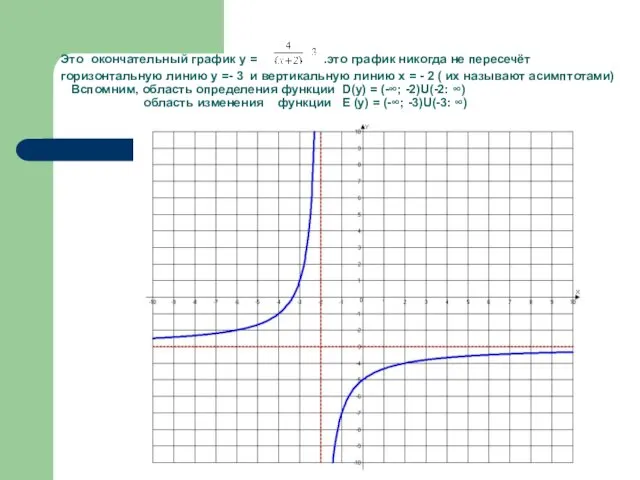
- 34. Это окончательный график у = .это график никогда не пересечёт горизонтальную линию у =- 3 и
- 35. В преобразовании у = f (x) в у = k f ( x + m )
- 37. Проверьте степень усвоения учебного материала, ответив на тесты. Нажмите клавишу Esc и заполните тесты. Сравните свои
- 38. B-1 русский яз B-2 украинский язык
- 39. Проверим результаты усвоения материала
- 40. B-1 B-2
- 42. Скачать презентацию











 Признаки параллельности двух прямых
Признаки параллельности двух прямых Свойства диагоналей четырехугольников
Свойства диагоналей четырехугольников Взаимно обратные числа
Взаимно обратные числа Геометрияның негізгі ұғымдары
Геометрияның негізгі ұғымдары Деление. Знак деления
Деление. Знак деления Вычитание числа 4
Вычитание числа 4 Сравнение по модулю m
Сравнение по модулю m История числа и цифры 1
История числа и цифры 1 Умножение обыкновенных дробей. Правила умножения
Умножение обыкновенных дробей. Правила умножения Занимательная математика для детей (устный счёт + учимся писать цифры)
Занимательная математика для детей (устный счёт + учимся писать цифры) История математики. Развитие и становление. Возникновение арифметики и геометрии
История математики. Развитие и становление. Возникновение арифметики и геометрии Базисная процедура. Линейность в переменных и параметрах
Базисная процедура. Линейность в переменных и параметрах Дискретные структуры. Теория множеств. Отношения
Дискретные структуры. Теория множеств. Отношения Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Көпжақтар
Көпжақтар Неизвестное об известных квадратных уравнениях
Неизвестное об известных квадратных уравнениях Средства измерений. Метрологические характеристики. Метрологические характеристики средств измерений
Средства измерений. Метрологические характеристики. Метрологические характеристики средств измерений Кому нужна математика
Кому нужна математика Тела вращения
Тела вращения Математические отношения
Математические отношения Циліндр, його елементи. Переріз площинами
Циліндр, його елементи. Переріз площинами Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов Случаи вычитания 15 -
Случаи вычитания 15 - Математика. Решение задач. 2 класс Школа России
Математика. Решение задач. 2 класс Школа России Презентация Урок математики в 4 классе
Презентация Урок математики в 4 классе Элементы дифференциального исчисления. Производые. Исследование (лекция 2)
Элементы дифференциального исчисления. Производые. Исследование (лекция 2) Третий признак равенства треугольников. Урок 21
Третий признак равенства треугольников. Урок 21 Координатная плоскость
Координатная плоскость