Содержание
- 2. Основная литература 1. Шипачев В. С. Высшая математика. Базовый курс: учебник и практикум для бакалавров [Гриф
- 3. Отчетность Контрольная работа №1 (рабочая программа, стр. 16-21, задачи с 1 по 6 включительно). Выполняется в
- 4. Основатели математической логики: – греческий философ Аристотеля (384–322 гг. до н.э.); – немецкий математик Готфрид Вильгельм
- 5. Математическая логика – это наука о средствах и методах математических доказательств. Алгебра логики применима к любым
- 6. На практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно
- 7. Высказывание – это утверждение о чем-либо, которое может быть либо истинным, либо ложным. Примеры высказываний: 1.
- 8. Истинные и ложные высказывания "Все учащиеся русской школы программистов умеют говорить по-русски". 2. "Основные предметы, преподаваемые
- 9. Повелительные, вопросительные, восклицательные и бессмысленные предложения не являются высказываниями «Уходя, гасите свет!» «Да здравствует мыло душистое
- 10. Высказывание, представляющее собой одно утверждение принято называть простым. Сложное высказывание получается путем объединения простых высказываний, связанных
- 11. Булевой функцией y=f(x1,x2,…,xn) от п переменных x1,x2,...,xn называется любая функция, в которой аргументы и функция могут
- 12. Отрицание (инверсия) . Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не
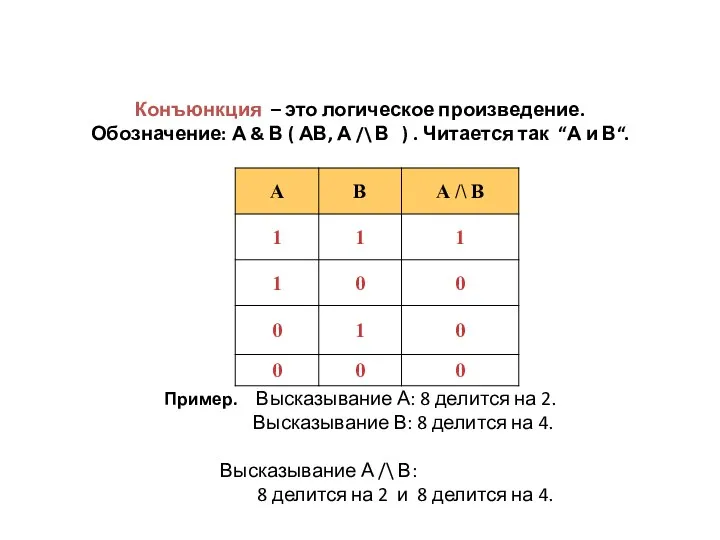
- 13. Конъюнкция – это логическое произведение. Обозначение: А & В ( АВ, А /\ В ) .
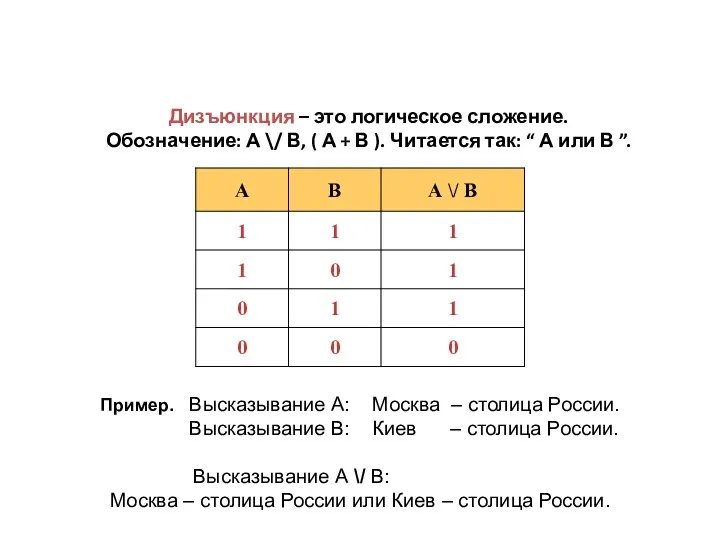
- 14. Дизъюнкция – это логическое сложение. Обозначение: А \/ В, ( А + В ). Читается так:
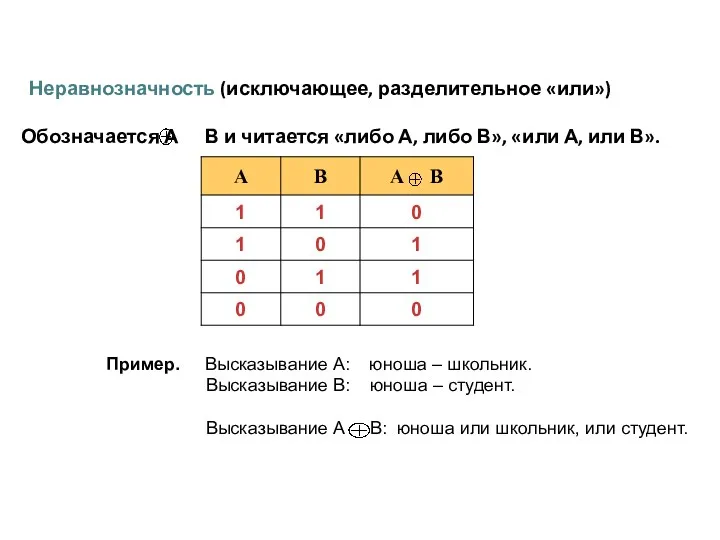
- 15. Неравнозначность (исключающее, разделительное «или») Обозначается А В и читается «либо А, либо В», «или А, или
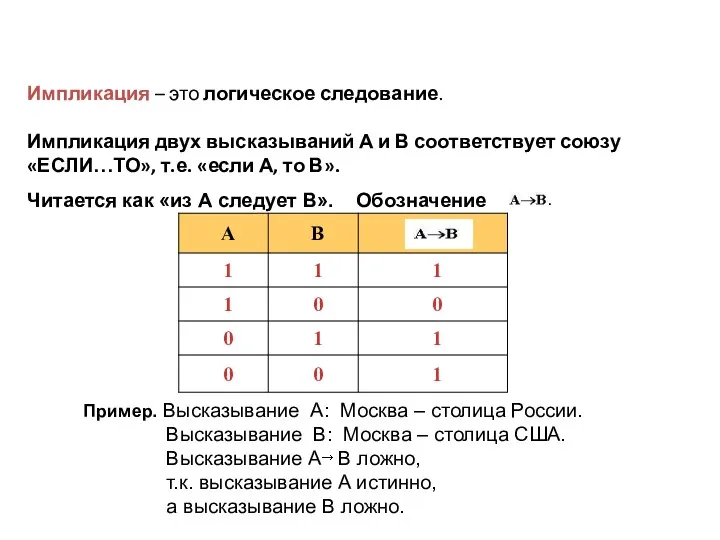
- 16. Импликация – это логическое следование. Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО», т.е. «если
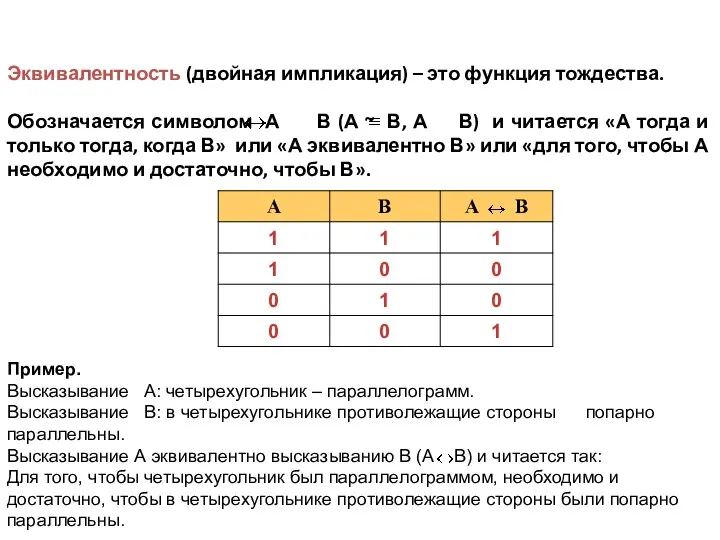
- 17. Эквивалентность (двойная импликация) – это функция тождества. Обозначается символом А В (А ~ В, А В)
- 18. С помощью алгебры логики над высказываниями можно выполнять следующие операции: из заданной совокупности элементарных высказываний строить
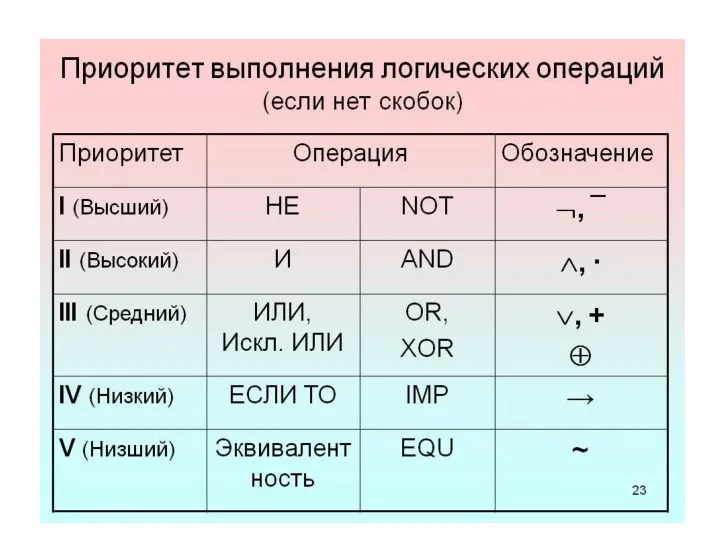
- 19. Порядок выполнения операций указывается скобками, которые можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем
- 20. СПАСИБО ЗА ВНИМАНИЕ!
- 21. Пример. Записать логической цепочкой следующее сложное высказывание: «Если спортсмен интенсивно тренируется и при этом принимает запрещенные
- 22. Переведем на язык алгебры логики следующее высказывание: 1. «Я поеду в Москву, и если встречу там
- 23. 3. «Если будет солнечная погода, то ребята пойдут в лес, а если будет пасмурная погода, то
- 24. 4. Если у меня будет свободное время и я сдам экзамены по педагогике и психологии, то
- 25. Интегральное исчисление функций одной переменной Первообразная и неопределенный интеграл
- 29. Свойства интеграла Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:
- 30. Свойства интеграла 3. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью
- 31. Свойства интеграла
- 32. Таблица неопределенных интегралов
- 33. Таблица неопределенных интегралов
- 34. Свойства дифференциалов При интегрировании удобно пользоваться свойствами:
- 35. Примеры
- 36. Примеры
- 37. Независимость от вида переменной
- 38. Пример Вычислим
- 39. Методы интегрирования Интегрирование по частям
- 40. Примеры
- 41. Примеры
- 42. Метод замены переменной
- 43. Интегрирование функций, содержащих квадратный трехчлен
- 44. Пример
- 45. Пример Найти
- 46. Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла. К понятию определенного интеграла приводит
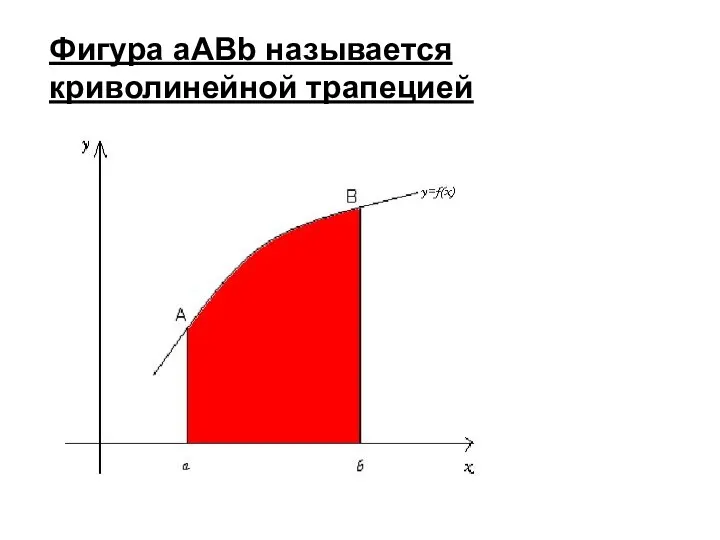
- 47. Фигура aABb называется криволинейной трапецией
- 48. Определение Под определенным интегралом от данной непрерывной функции f(x) на данном отрезке [a;b] понимается соответствующее приращение
- 49. Правило: Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования. Введя
- 50. Основные свойства определенного интеграла. 1)Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. где x
- 51. 3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный (свойство аддитивности) 4) Если
- 52. 5)Постоянный множитель можно выносить за знак определенного интеграла. 6)Определенный интеграл от алгебраической суммы конечного числа непрерывных
- 53. 3. Замена переменной в определенном интеграле. где для , функции и непрерывны на Пример: = =
- 54. Несобственные интегралы. Определение. Пусть функция f(x) определена на бесконечном интервале [a; + ∞) и интегрируется на
- 55. Таким образом, по определению, Если этот предел - некоторое число, то интеграл называется сходящимся, если предела
- 56. Пример. Интеграл Пуассона: если а = 1, то Интеграл сходится, и его значение .
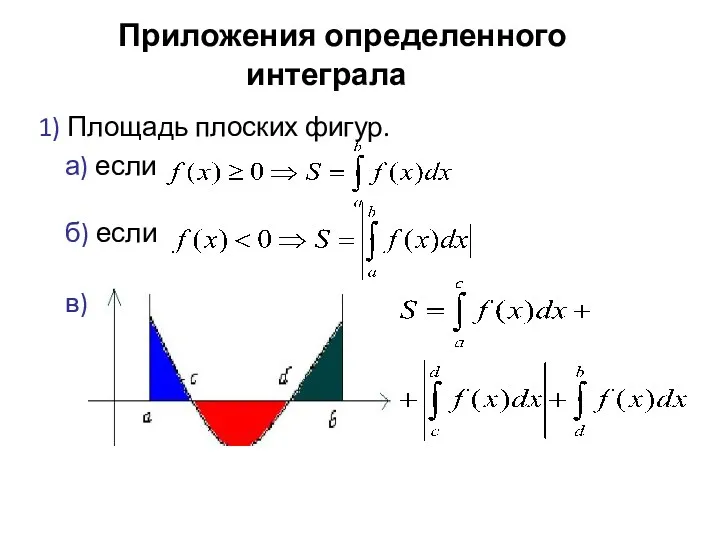
- 57. 5. Приложения определенного интеграла 1) Площадь плоских фигур. а) если б) если в)
- 58. г) 2) Многие физические величины можно определить и задать через понятие интеграла. Например, работа для любой
- 59. 1. Основные определения Числовые и функциональные ряды
- 60. Основные определения
- 61. 2. Числовые ряды с неотрицательными членами
- 62. Числовые ряды с неотрицательными членами
- 63. Числовые ряды с неотрицательными членами
- 64. Числовые ряды с неотрицательными членами
- 65. Числовые ряды с неотрицательными членами
- 66. 3. Знакопеременные ряды, абсолютная сходимость
- 67. Знакопеременные ряды, абсолютная сходимость
- 68. Знакопеременные ряды, абсолютная сходимость
- 69. 1. Степенные ряды, радиус сходимости Степенные ряды
- 70. Степенные ряды, радиус сходимости
- 71. 2. Ряд Тейлора
- 72. Ряд Тейлора
- 73. Ряд Тейлора. Разложение в степенной ряд элементарных функций
- 74. Ряд Тейлора. Разложение в степенной ряд элементарных функций
- 75. Ряд Тейлора. Разложение решения дифференциального уравнения в степенной ряд
- 76. Ряд Тейлора. Разложение решения дифференциального уравнения в степенной ряд
- 78. Скачать презентацию







































![Определение Под определенным интегралом от данной непрерывной функции f(x) на данном отрезке [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/586748/slide-47.jpg)



























 Презентация к уроку математики в 1 классе Сложение и вычитание в пределах 20
Презентация к уроку математики в 1 классе Сложение и вычитание в пределах 20 Презентация по математике Умножение в Простоквашино
Презентация по математике Умножение в Простоквашино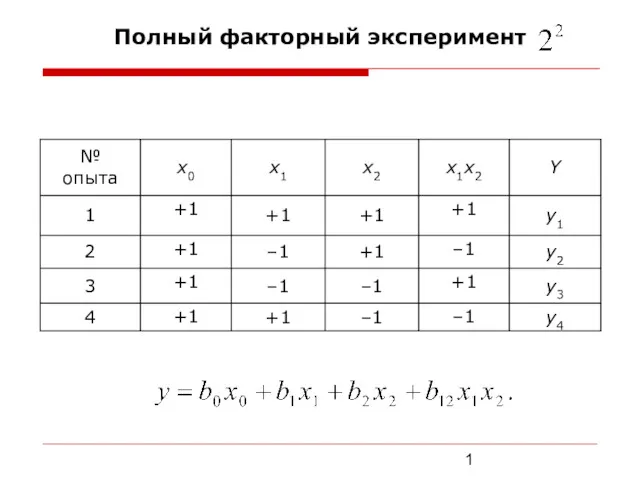 Полный факторный эксперимент
Полный факторный эксперимент Применение основных тригонометрических тождеств для преобразования выражений
Применение основных тригонометрических тождеств для преобразования выражений Деление и умножение трехзначных чисел (устные вычисления).
Деление и умножение трехзначных чисел (устные вычисления). Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану
Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану презентация к уроку Умножение на однозначное число.
презентация к уроку Умножение на однозначное число. Формулирование факторов для использования их в статистической модели
Формулирование факторов для использования их в статистической модели История появления математики
История появления математики Уравнения
Уравнения Теорема про три перпендикуляри
Теорема про три перпендикуляри Задачи о земледелии в горных районах. Решение практико-ориентированных задач
Задачи о земледелии в горных районах. Решение практико-ориентированных задач Великие математические умы
Великие математические умы Рациональные дроби и их свойства
Рациональные дроби и их свойства Математические задачи в стихах
Математические задачи в стихах Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Решение логических задач
Решение логических задач презентация к конспекту по математике Диск
презентация к конспекту по математике Диск Сложение натуральных чисел и его свойства. 5 класс
Сложение натуральных чисел и его свойства. 5 класс Промежутки возрастания и убывания функции. Точки экстремума
Промежутки возрастания и убывания функции. Точки экстремума Математика. 1 класс. Урок 15. Равенства и неравенства. Презентация
Математика. 1 класс. Урок 15. Равенства и неравенства. Презентация Математическая раскраска Колобок
Математическая раскраска Колобок Средняя линия треугольника
Средняя линия треугольника Метрология — наука об измерениях, методах и средствах обеспечения их единства
Метрология — наука об измерениях, методах и средствах обеспечения их единства Цилиндр. Решение задач
Цилиндр. Решение задач Урок закрепления по теме : Сложение и вычитание вида +1,-1.
Урок закрепления по теме : Сложение и вычитание вида +1,-1. Обобщающий урок по теме: Треугольники
Обобщающий урок по теме: Треугольники ОФОРМЛЕНИЕ ПИСЬМЕННЫХ РАБОТ ПО МАТЕМАТИКЕ
ОФОРМЛЕНИЕ ПИСЬМЕННЫХ РАБОТ ПО МАТЕМАТИКЕ