Содержание
- 2. История симплекс-метода Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в
- 3. Решение задачи симплекс-методом Пусть x1, x2, x3 - количество реализованных товаров, в тыс. руб., 1, 2,
- 4. В качестве базиса возьмем x4 = 240; x5 = 200; x6 = 160. Данные заносим в
- 5. Вычисляем оценки по формуле: Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка: Δ2 =
- 6. Выводим переменную x6 из базиса
- 7. Получаем новую таблицу: Симплекс таблица № 2
- 8. Поскольку есть отрицательная оценка Δ1 = – 2/3, то план не оптимален. Вводим переменную x1 в
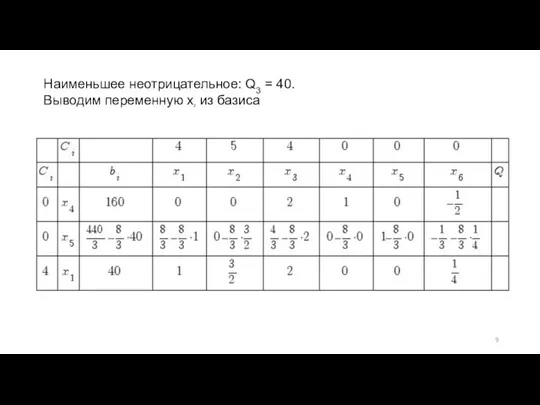
- 9. Наименьшее неотрицательное: Q3 = 40. Выводим переменную x2 из базиса
- 10. Получаем новую симплекс – таблицу 3
- 11. Поскольку отрицательных оценок нет, то план оптимален. Решение задачи: x1 = 40; x2 = 0; x3
- 12. На основе симплекс-метода задачу можно продолжить решать с помощью следующих методов Значительная часть задач, относящихся к
- 13. Метод Гомори Идея: если добавить новые ограничения, связывающие граничные целочисленные точки, а затем в качестве многогранника
- 14. Метод ветвей и границ Суть: упорядоченный перебор вариантов и рассмотрение лишь тех из них, которые оказываются
- 15. Условия задачи Найти оптимальное решение стандартной задачи максимизации для целевой функции L= X1 + 3Х2 +
- 16. Ответ Соответствующее значение целевой функции равно Lmax = 4 X = (1, 1, 0)
- 18. Скачать презентацию














 Метод математических моделей в экономике
Метод математических моделей в экономике Викторина по математике для 6 класса (итоги года)
Викторина по математике для 6 класса (итоги года) Закрепление + - 3. Сравнение отрезков. 1 класс Школа России
Закрепление + - 3. Сравнение отрезков. 1 класс Школа России Координаты на прямой. 6 класс
Координаты на прямой. 6 класс Ықтималдық теориясы.математикалық статистика
Ықтималдық теориясы.математикалық статистика Презентация СПОСОБ СЛОЖЕНИЯ СТОЛБИКОМ. СЛОЖЕНИЕ ДВУЗНАЧНЫХ И ТРЕХЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ ЧЕРЕЗ РАЗРЯД
Презентация СПОСОБ СЛОЖЕНИЯ СТОЛБИКОМ. СЛОЖЕНИЕ ДВУЗНАЧНЫХ И ТРЕХЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ ЧЕРЕЗ РАЗРЯД Вопросы к экзамену
Вопросы к экзамену Correlation and Regression
Correlation and Regression Аксиомы параллельных прямых
Аксиомы параллельных прямых Каллиграфия цифр. Математика для начальных классов
Каллиграфия цифр. Математика для начальных классов Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Сравнение дробей с разными знаменателями
Сравнение дробей с разными знаменателями Презентация+конспект урока по математике. 1 класс. Составление и решение задач
Презентация+конспект урока по математике. 1 класс. Составление и решение задач Помощь учащимся при подготовке к ЕГЭ по математике
Помощь учащимся при подготовке к ЕГЭ по математике Математическая викторина для 5-7 класса
Математическая викторина для 5-7 класса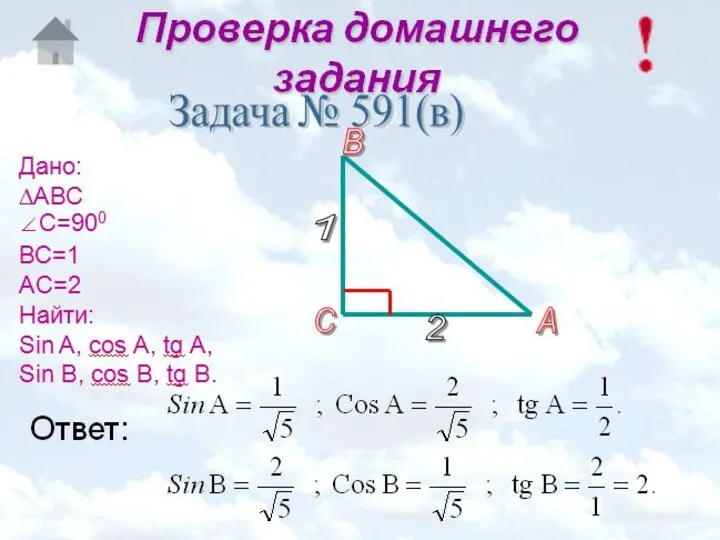 Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. Решение задач по готовым чертежам
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. Решение задач по готовым чертежам Степенные функции, их свойства и графики. Урок алгебры в 11 классе
Степенные функции, их свойства и графики. Урок алгебры в 11 классе Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Порівняння чисел. Задачі на зменшення числа на кілька одиниць (урок № 75)
Порівняння чисел. Задачі на зменшення числа на кілька одиниць (урок № 75) Математика в подготовительной группе
Математика в подготовительной группе Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Многогранник - геометрическое тело
Многогранник - геометрическое тело Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач
Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач Математика в строительстве
Математика в строительстве Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Математическая игра ДМШата в стране математики
Математическая игра ДМШата в стране математики Теория предельной полезности и поведения потребителя
Теория предельной полезности и поведения потребителя Математический диктант
Математический диктант