Содержание
- 2. «НЕТ НИ ОДНОЙ ОБЛАСТИ МАТЕМАТИКИ, КАК БЫ АБСТРАКТНА ОНА НИ БЫЛА, КОТОРАЯ КОГДА-НИБУДЬ НЕ ОКАЖЕТСЯ ПРИМЕНИМОЙ
- 3. ЦЕЛИ ЗАНЯТИЯ: узнать историю открытия производной; узнать основные направления применения производной в разных областях науки и
- 4. НЕМНОГО ИЗ ИСТОРИИ Производная – одно из фундаментальных понятий математики, характеризующее скорость изменения функции в данной
- 10. ПРИРАЩЕНИЕ АРГУМЕНТА, ПРИРАЩЕНИЕ ФУНКЦИИ. Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х0.
- 12. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Если функции u и v дифференцируемы в точке х0, то справедливы следующие правила:
- 13. ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 14. ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ. Решая примеры, проговаривайте вслух. Помните: «Мысль рождается с собственной речи!»
- 15. ТЕСТ ПО ТЕМЕ «ПРОИЗВОДНАЯ ФУНКЦИИ»
- 16. 1. Выражение вида Δf появилось уже в конце 17 в. и означает «приращение». 2. Термин производная
- 17. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Геометрический смысл производной со- стоит в том, что производная в точке х0 равна
- 19. Уравнение касательной y = f / (x0) · (x - x0) + f(x0) (x0; f(x0)) –
- 20. Найдите угловой коэффициент касательной к кривой в точке с абсциссой х0= - 2.
- 21. Алгоритм нахождения уравнения касательной к графику функции y=f(x). Вычислим . Найдем Вычислим Подставим найденные числа a
- 22. К ГРАФИКУ ФУНКЦИИ В ТОЧКЕ СОСТАВИТЬ УРАВНЕНИЕ КАСАТЕЛЬНОЙ.
- 23. МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ (ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ) Механический смысл производной состоит в том, что производная пути по
- 24. РЕШАЕМ ЗАДАЧИ! Точка движется по закону а) выведите формулу для вычисления скорости движения точки в любой
- 25. а) V(t) = - t 2 + 4 t + 5. б) V(2) = - 2
- 26. Материальная точка движется прямолинейно по закону x(t) = t 3 – 4 t 2 Перемещение измеряется
- 27. Решение. V(t) = x′(t) = 3 t 2 - 8 t ; V(5) = 3 ∙
- 28. ОТВЕТИМ НА СЛЕДУЮЩИЕ ВОПРОСЫ: Сформулируйте определение производной функции? Как называется математическая операция нахождения производной функции? В
- 30. Скачать презентацию




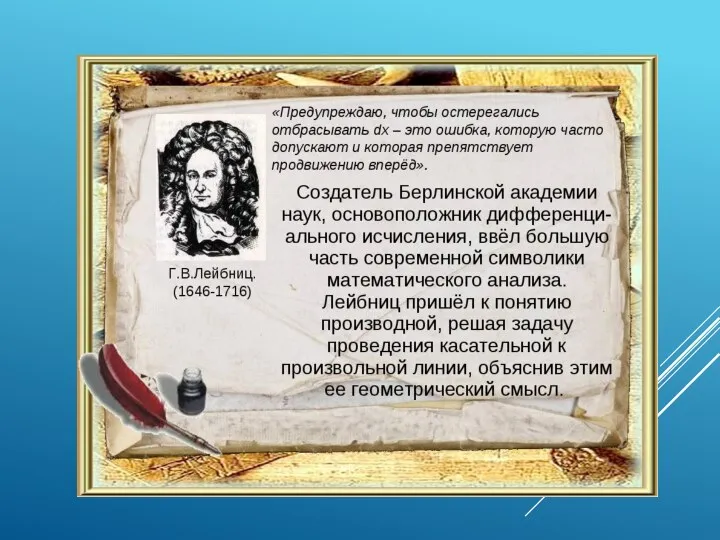














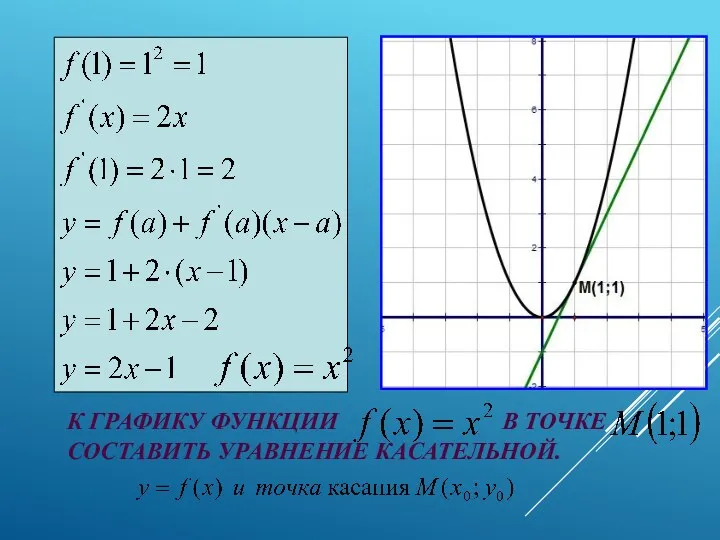




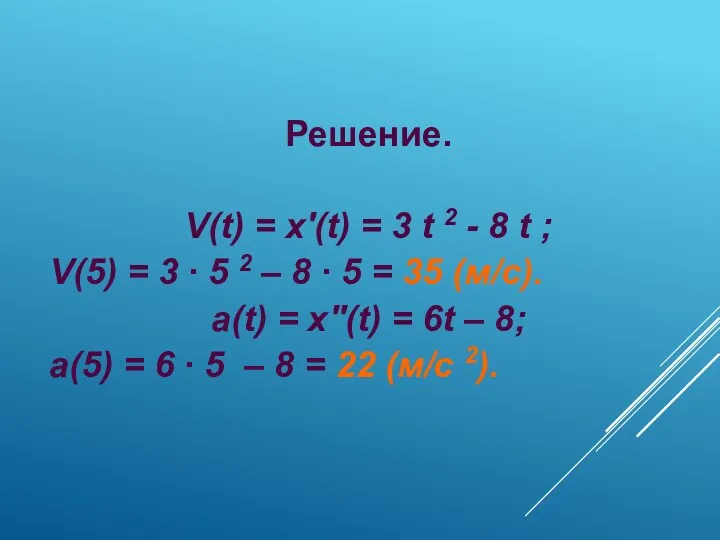

 Таблица умножения двух
Таблица умножения двух Образование чисел из одного десятка и нескольких единиц. 1 класс
Образование чисел из одного десятка и нескольких единиц. 1 класс Деление дробей. Урок 127
Деление дробей. Урок 127 Урок Сложение двузначных чисел в столбик, технология проблемного обучения
Урок Сложение двузначных чисел в столбик, технология проблемного обучения Тест по логике № 1. Тема Понятие
Тест по логике № 1. Тема Понятие тренажёр по математике 1 класс
тренажёр по математике 1 класс Линейная функция и её график
Линейная функция и её график О проверке статистических гипотез
О проверке статистических гипотез Логарифмические уравнения. Уравнения, решаемые с использованием теорем о логарифмах
Логарифмические уравнения. Уравнения, решаемые с использованием теорем о логарифмах Действия с геометрическими фигурами. Прототип задания B3, ЕГЭ
Действия с геометрическими фигурами. Прототип задания B3, ЕГЭ Математика. 1 класс. Урок 86. Числа от 10 до 20 - Презентация
Математика. 1 класс. Урок 86. Числа от 10 до 20 - Презентация Признаки параллельности прямых
Признаки параллельности прямых Симметрия
Симметрия Замечательные точки треугольника. Урок 1. Свойство биссектрисы угла
Замечательные точки треугольника. Урок 1. Свойство биссектрисы угла Окружность. Радиус и диаметр окружности
Окружность. Радиус и диаметр окружности Комплексные числа. Основные понятия. Формы записи
Комплексные числа. Основные понятия. Формы записи Решение задач. Урок математики для 4 класса
Решение задач. Урок математики для 4 класса Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Свойства параллелограмма
Свойства параллелограмма Тела вращения. Цилиндр
Тела вращения. Цилиндр Слайд-шоу с методическим сопровождениемВ царстве геометрических фигур
Слайд-шоу с методическим сопровождениемВ царстве геометрических фигур Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Порядок действий в примерах со скобками. Презентация
Порядок действий в примерах со скобками. Презентация Комбинация призмы и цилиндра
Комбинация призмы и цилиндра Разработка урока математики Вычитание числа 1 1 класс
Разработка урока математики Вычитание числа 1 1 класс Тригонометрические формулы
Тригонометрические формулы Тела вращения
Тела вращения Презентация к уроку математики 2 кл. Угол. Виды углов и треугольников.
Презентация к уроку математики 2 кл. Угол. Виды углов и треугольников.