Содержание
- 2. Происхождение производной. Первую задачу: о связи скорости и пути прямолинейно и неравномерно движущейся точки впервые решил
- 3. Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке х этого
- 4. Нахождение производной называют дифференцированием
- 5. Таблица производных
- 6. Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 7. Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 8. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 9. Примеры
- 10. Примеры
- 11. подсказка Тело, подброшенное вверх движется по закону s(t) = 4+ 8t – 5t 2 . Найдите:
- 12. ЗАДАЧА №2 При каких значениях х значение производной функции равно 0
- 13. Примеры
- 15. Производная и ее применение
- 16. Правильный ответ Правильный ответ Правильный ответ Правильный ответ Правильный ответ Найдите производные функций:
- 17. Найдите производную функции(устно): а) у = 6х5 – 7х3 + 2х2 – 5, у/ = 30
- 18. Найдите производную функции(устно): Правильный ответ Правильный ответ Правильный ответ Правильный ответ
- 20. 3. 4. 5.
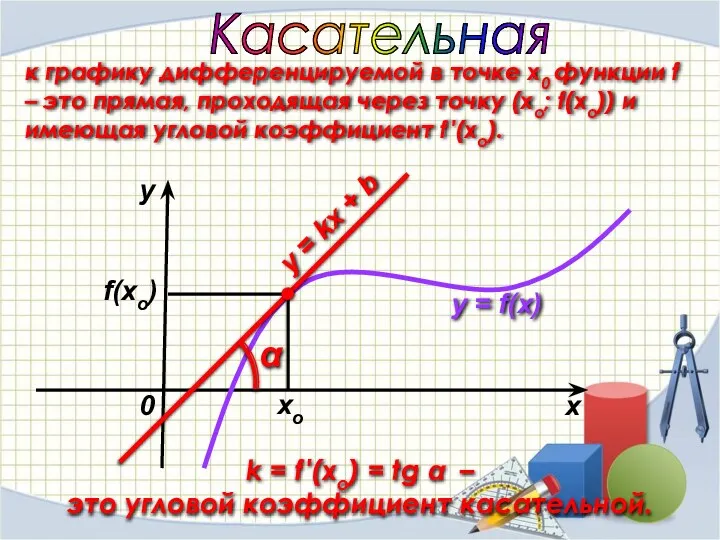
- 21. k = f ′(xo) = tg α – это угловой коэффициент касательной. f(xo) Касательная к графику
- 22. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 23. Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания. Признак возрастания
- 24. Алгоритм решения неравенств методом интервалов: Выделить функцию y=f(x). Найти область определения функции D(f). Указать промежутки непрерывности.
- 25. Решите неравенство: 1. 2x+5≠0, х ≠-2,5 2. f(x)=0, если x1= 8, x2= -2 3. Ответ:
- 26. Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x): Найти производную функции f´(x). Решить уравнение f´ (x) =0.
- 27. Найдите промежутки возрастания и убывания функции: 1. 2. f´(x)=0, если 3. Ответ:
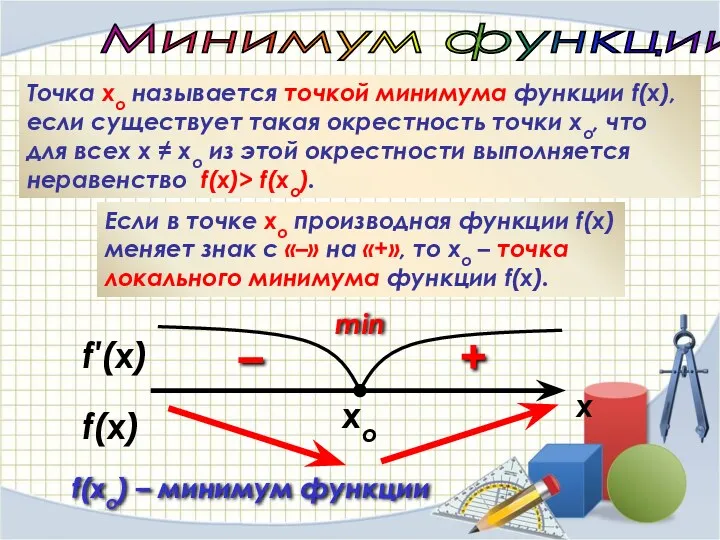
- 28. f′(x) xo Минимум функции Точка хо называется точкой минимума функции f(x), если существует такая окрестность точки
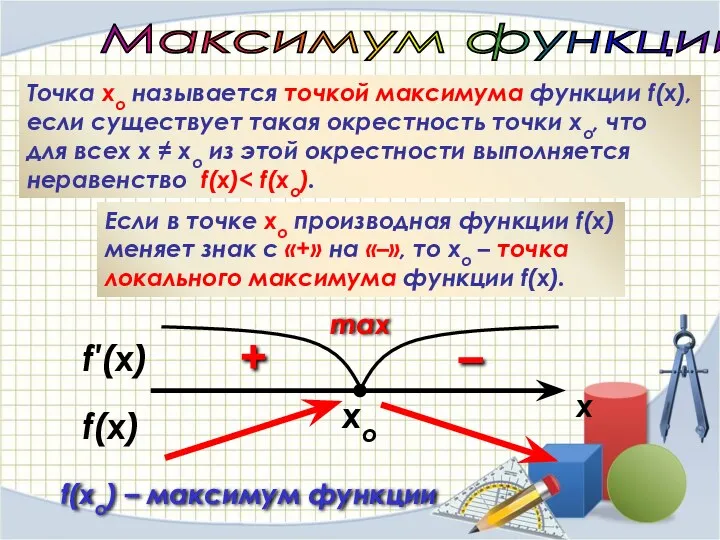
- 29. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
- 30. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
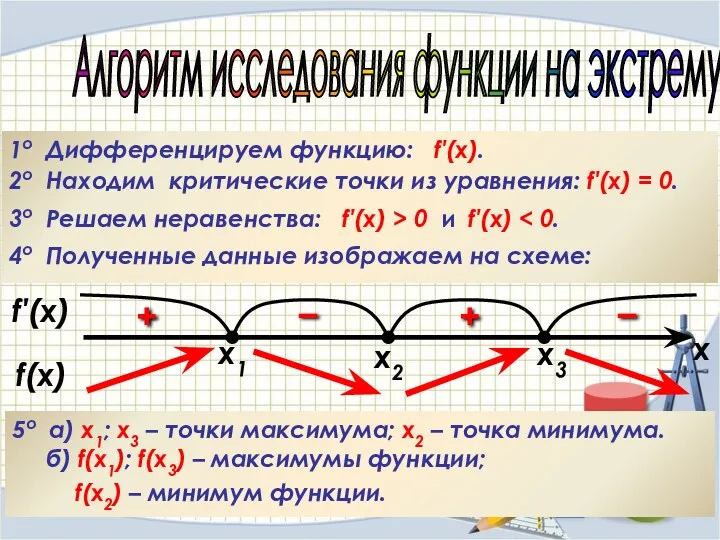
- 31. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 32. Примеры
- 34. + + + – –
- 36. Скачать презентацию





























 Уравнение прямой на плоскости
Уравнение прямой на плоскости Параллельные прямые. Урок геометрии в 7 классе
Параллельные прямые. Урок геометрии в 7 классе Многомерный анализ данных ( лекция 9)
Многомерный анализ данных ( лекция 9) Презентация: Деление многозначного числа с нулём на конце делимого(и остатком).
Презентация: Деление многозначного числа с нулём на конце делимого(и остатком). Додавання і віднімання по одному і частинами. Задачі на знаходження суми
Додавання і віднімання по одному і частинами. Задачі на знаходження суми Вступ до математичного аналізу
Вступ до математичного аналізу Умножение дробей. Нахождение дроби от числа. Обобщающий урок -экскурсия
Умножение дробей. Нахождение дроби от числа. Обобщающий урок -экскурсия Множественный корреляционный анализ
Множественный корреляционный анализ Понятие эксперимента. Классификация видов экспериментальных исследований
Понятие эксперимента. Классификация видов экспериментальных исследований Диаметр окружности. Круг. К уроку №59. Математика. 3 класс
Диаметр окружности. Круг. К уроку №59. Математика. 3 класс Решение нестандартных задач по математике
Решение нестандартных задач по математике Пропорциональные величины. Решение задач
Пропорциональные величины. Решение задач Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Касательная. Уравнение касательной
Касательная. Уравнение касательной Сложение двузначных чисел. (2 класс)
Сложение двузначных чисел. (2 класс) Среднее арифметическое
Среднее арифметическое Делители и кратные
Делители и кратные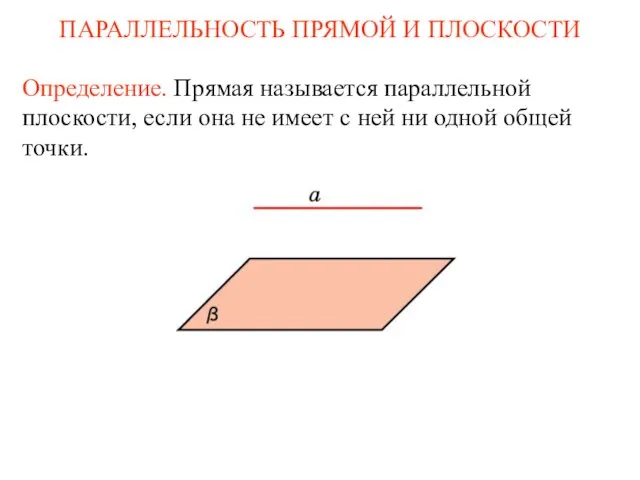 Параллельность прямой и плоскости
Параллельность прямой и плоскости Статистические характеристики
Статистические характеристики Объем пирамиды. Инструкция по решению задач
Объем пирамиды. Инструкция по решению задач Проектная задача
Проектная задача Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Невизначений інтеграл, його властивості і обчислення
Невизначений інтеграл, його властивості і обчислення Прямая призма. Решение задач
Прямая призма. Решение задач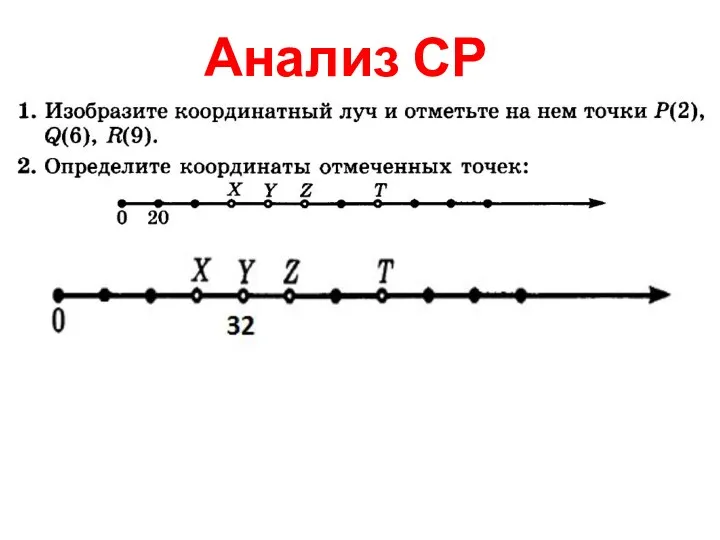 Обозначения натуральных чисел. Меры длины и массы. Луч, прямая, отрезок
Обозначения натуральных чисел. Меры длины и массы. Луч, прямая, отрезок Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Счёт в пределах 100 Помоги Незнайке
Счёт в пределах 100 Помоги Незнайке Конструкт урока по математике. Решение уравнений
Конструкт урока по математике. Решение уравнений