Содержание
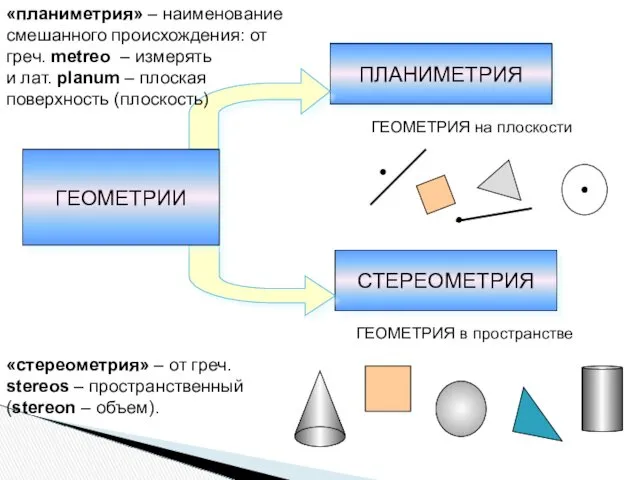
- 2. ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ ГЕОМЕТРИЯ на плоскости ГЕОМЕТРИЯ в пространстве «планиметрия» – наименование смешанного происхождения: от греч. metreo
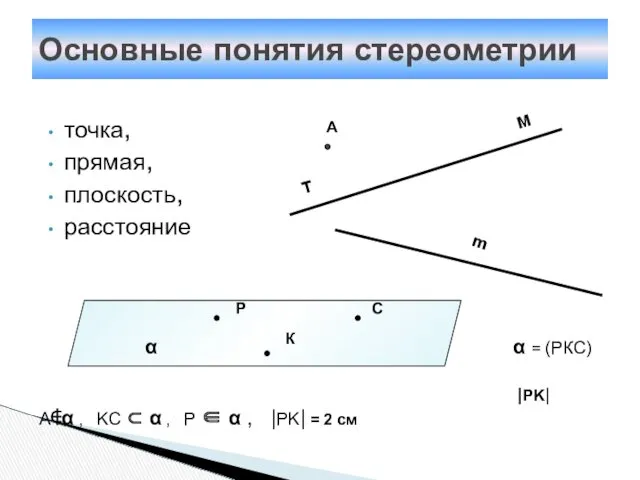
- 3. точка, прямая, плоскость, расстояние Основные понятия стереометрии α = (РКС) |PK| A∉α , KC ⊂ α
- 4. ВСПОМНИМ ПЛАНИМЕТРИЮ Каково может быть взаимное расположение двух прямых на плоскости? Какие прямые в планиметрии называются
- 5. ВСПОМНИМ ПЛАНИМЕТРИЮ Аксиома параллельных прямых - ? Через точку, не лежащую на данной прямой, проходит прямая,
- 6. ВСПОМНИМ ПЛАНИМЕТРИЮ Следствия аксиомы параллельных прямых - ? Если прямая пересекает одну из параллельных прямых, то
- 7. Аксиомы стереометрии А-1 Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом
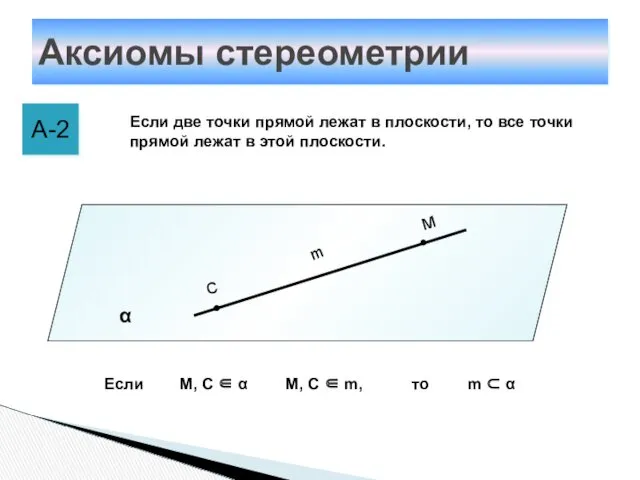
- 8. Аксиомы стереометрии А-2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в
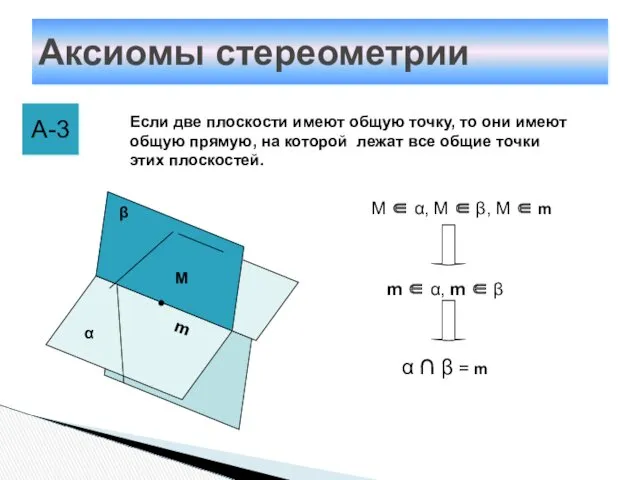
- 9. Аксиомы стереометрии А-3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой
- 10. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
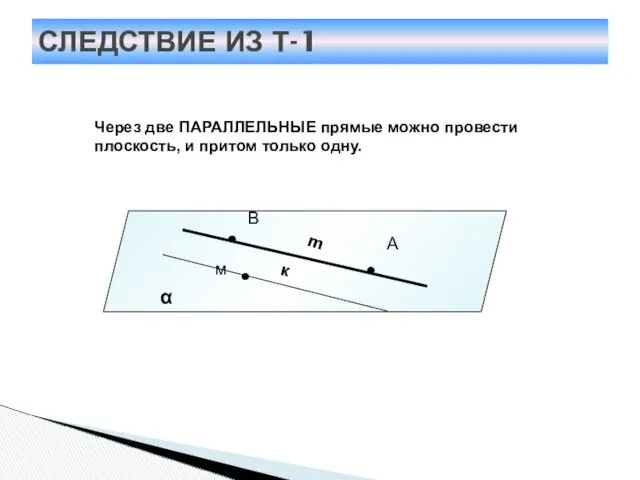
- 11. СЛЕДСТВИЕ ИЗ Т-1 Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну. к
- 12. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
- 13. По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой
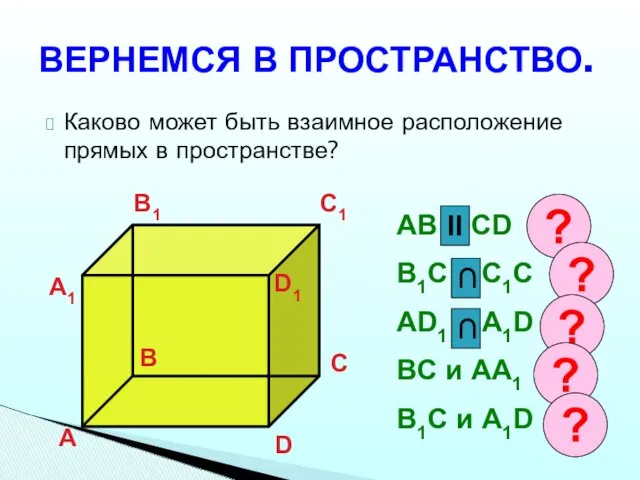
- 14. ВЕРНЕМСЯ В ПРОСТРАНСТВО. Каково может быть взаимное расположение прямых в пространстве? А B C D А1
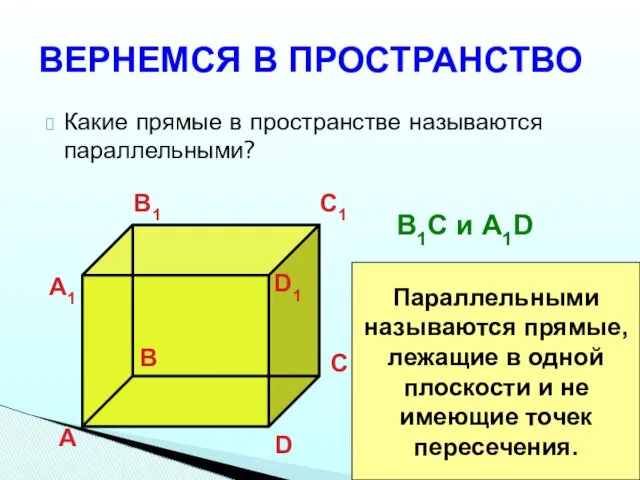
- 15. ВЕРНЕМСЯ В ПРОСТРАНСТВО Какие прямые в пространстве называются параллельными? А B C D А1 B1 C1
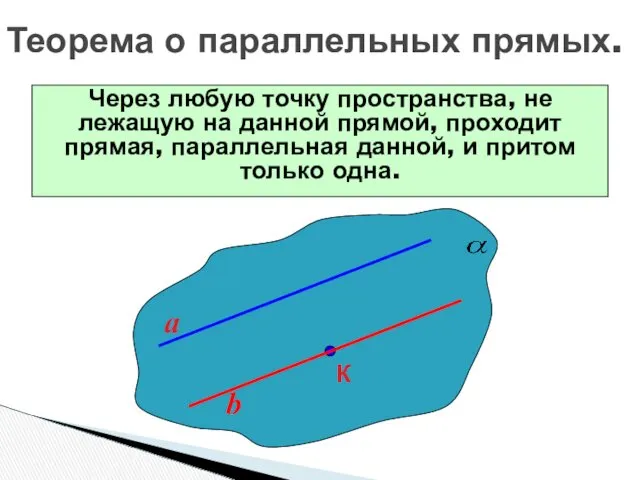
- 16. Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная
- 17. …они лежат на параллельных прямых Отрезки в пространстве называются параллельными, если … Лучи в пространстве называются
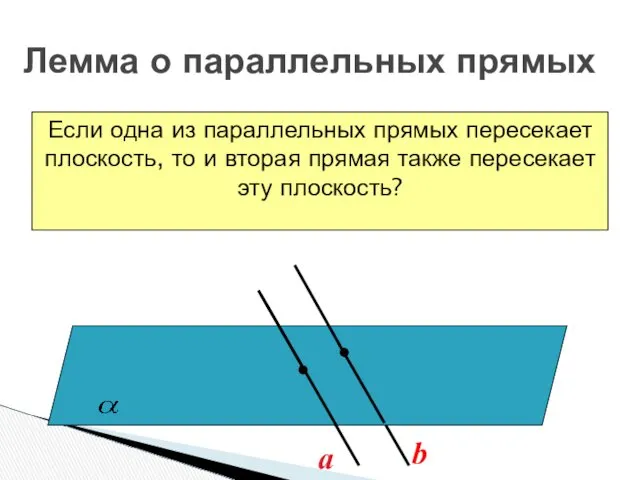
- 18. Лемма о параллельных прямых Если одна из параллельных прямых пересекает плоскость, то и вторая прямая также
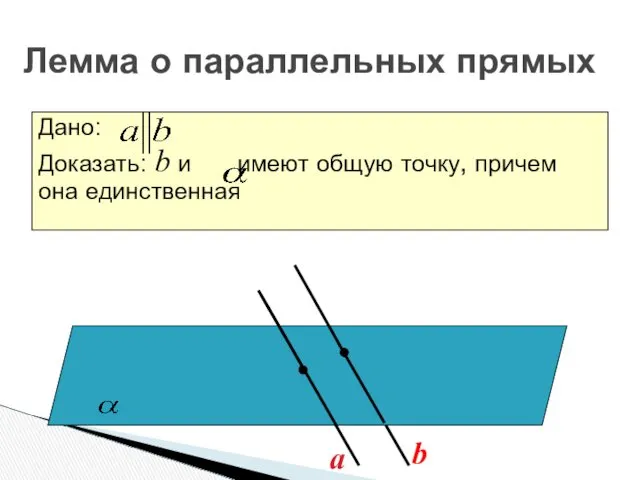
- 19. Лемма о параллельных прямых Дано: Доказать: b и имеют общую точку, причем она единственная a b
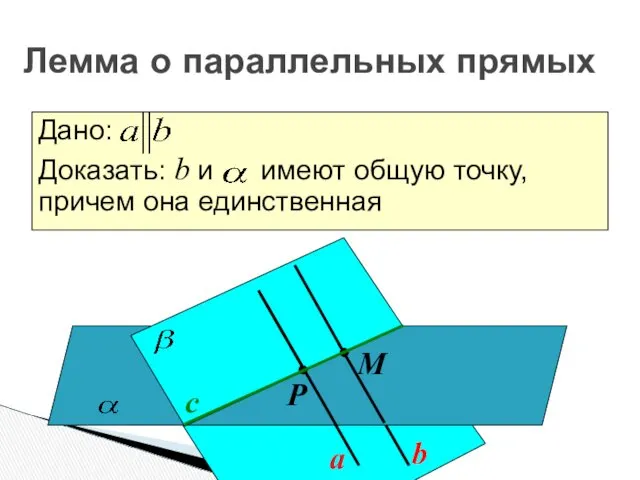
- 20. a b с Р М Дано: Доказать: b и имеют общую точку, причем она единственная Лемма
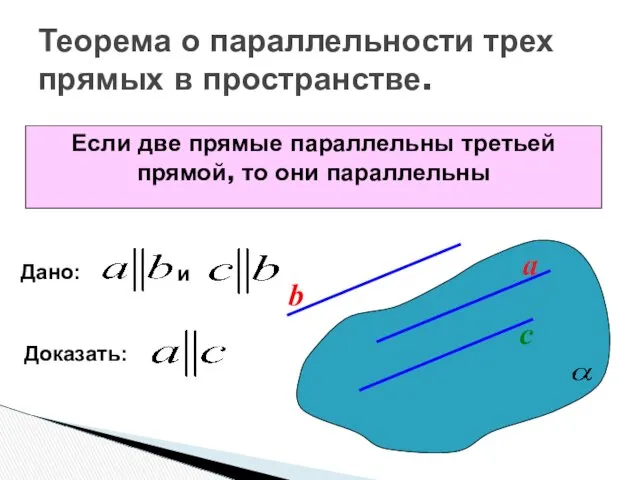
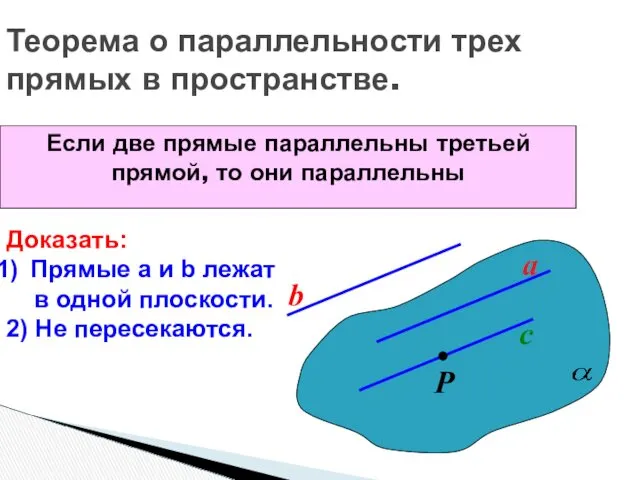
- 21. Теорема о параллельности трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны
- 22. Теорема о параллельности трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны
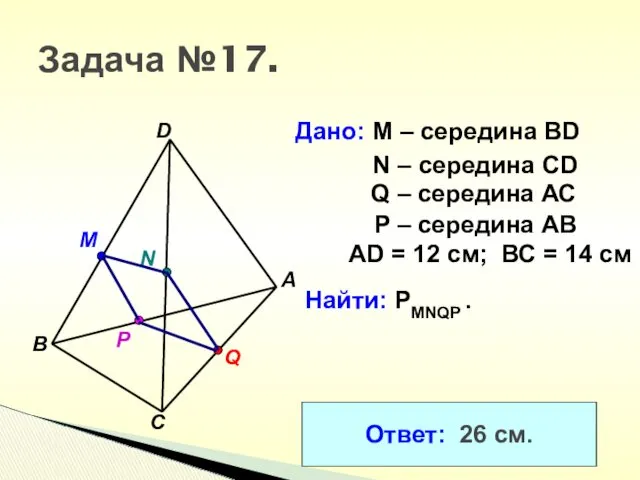
- 23. Задача №17. Дано: М – середина BD A B D C N M Р Q N
- 25. Скачать презентацию








 Вычитание удобным способом
Вычитание удобным способом Признаки деления на 3, на 9
Признаки деления на 3, на 9 Физкультминутка(презентация)
Физкультминутка(презентация) Транспортная задача
Транспортная задача Некоторые свойства прямоугольного треугольника. Урок 47
Некоторые свойства прямоугольного треугольника. Урок 47 Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения устный счет
устный счет Сумматор
Сумматор Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Свойства функции. 10 класс
Свойства функции. 10 класс Геометрический смысл производной. Подготовка к ЕГЭ
Геометрический смысл производной. Подготовка к ЕГЭ Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Счастливый случай. Игра
Счастливый случай. Игра Инновационный опыт
Инновационный опыт Задачи на нахождение значений параметра
Задачи на нахождение значений параметра Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Прямоугольная система координат на плоскости. 6 класс
Прямоугольная система координат на плоскости. 6 класс Ряд натуральных чисел
Ряд натуральных чисел Многогранники и их виды
Многогранники и их виды Понятие движения в геометрии
Понятие движения в геометрии Системы двух уравнений с двумя неизвестными. 7 класс
Системы двух уравнений с двумя неизвестными. 7 класс Треугольники. Виды треугольников. Основные свойства треугольников
Треугольники. Виды треугольников. Основные свойства треугольников Decimals
Decimals Взаимно простые числа. Признак делимости на произведение
Взаимно простые числа. Признак делимости на произведение Сложение и вычитание векторов
Сложение и вычитание векторов устный счёт в виде теста 2 класс Табличное умножение
устный счёт в виде теста 2 класс Табличное умножение Перпендикулярные прямые. Решение задач
Перпендикулярные прямые. Решение задач