Содержание
- 2. Маршрут урока:
- 3. Иррациональными называются уравнения, в которых переменная содержится под знаком корня (радикала) или под знаком операции возведения
- 4. Основная идея при решении уравнений данного типа – это освобождение их от иррациональности. Ее можно достичь
- 5. Либо путем извлечения корня из соответствующей степени выражения.
- 6. При возведении обеих частей уравнения в нечетную степень (3,5,7,..) выполняется равносильное преобразование уравнения, поэтому посторонние решения
- 7. Пример решения уравнения: Ответ: 0; 1.
- 8. Возведение обеих частей уравнения в одну и ту же четную степень является неравносильным преобразованием уравнений, поэтому
- 9. Для отсеивания посторонних корней необходимо выполнять проверку или находить ОДЗ. Рассмотрим примеры решения подобных уравнений:
- 10. Возведем обе части уравнения в квадрат:
- 11. Выполним проверку: Ответ: 2.
- 12. Найдем ОДЗ: 5 х
- 13. Аналогично рассмотренному примеру возведем обе части уравнения в квадрат и решим уравнение:
- 16. Также при решении иррациональных уравнений необходимо учитывать не равносильность преобразований корня четной степени вида:
- 17. При разбиении подкоренного выражения возможна потеря корней из-за сужения ОДЗ.
- 18. При слиянии корней возможно получение посторонних корней из-за расширения исходного ОДЗ. Посторонние корни, которые появляются при
- 19. Алгоритм решения иррациональных уравнений основными методами: Найти ОДЗ или после нахождения корней уравнения выполнить проверку. Возвести
- 20. Методы решения иррациональных уравнений: Уединение корня в одной из частей уравнения, а потом возведение обеих частей
- 21. Уединение корня в одной из частей уравнения, а потом возведение обеих частей уравнения в одну и
- 22. Возведем обе части в квадрат и приравняем уравнение к нулю. Ответ: 0.
- 23. Введение новой переменной и решение полученного уравнения любым из известных методов. Решить уравнение: Возведем обе части
- 24. Возвращаясь к исходной переменной получаем уравнение: Ответ: -1; 2.
- 25. Умножение на сопряженное выражение. Решить уравнение:
- 26. Итак, левая часть уравнения равна 6х, значит наше уравнение принимает вид: то есть оно имеет решения,
- 27. Для упрощения решения, сложим полученное и исходное уравнения, в итоге получаем уравнение следствие: Решаем его методом
- 28. Метод применения свойств функции. № 1. Решить уравнение: (При решении данного уравнения основными методами необходимо будет
- 29. Метод применения свойств функции. № 2. Решить уравнение: (Попытка решить данное уравнение основными методами к успеху
- 30. Значит, данное уравнение, имеет корни только из данного промежутка. Проверяя целые значения (1,2,3) , находим, что
- 31. Уравнения приводимые к уравнениям с модулями. Решить уравнение: Каждое подкоренное выражение можно свернуть, как квадрат двучлена:
- 32. При уравнение принимает вид: При уравнение принимает вид: откуда откуда и не имеет корней. Ответ: -6;
- 33. Искусственные приемы решения иррациональных уравнений. Решить уравнение: Уединение корня и возведение обеих частей уравнения в квадрат
- 34. Введем новую переменную, пусть Получаем квадратное уравнение Его корни: Значит, исходное уравнение равносильно совокупности:
- 35. Второе уравнение корней не имеет, а из первого следует, что корни уравнения равны: Так как совокупность
- 36. Примеры для самостоятельного решения дома:
- 37. Если натуральные числа возникли в процессе счета, а рациональные — из потребности оперировать частями целого, то
- 39. Несоизмеримые величины, были названы еще в древности иррациональными. Первоначально термины “рациональный” и “иррациональный” относились не к
- 40. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число
- 41. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими
- 42. Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных
- 43. В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об
- 45. Современный знак корня произошел от обозначения, примяемого немецкими математиками XV-XVI вв.: Скорее всего, в последствии от
- 46. Автором этого знака был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Эти знаком пользовались А.Жирар,
- 47. Такая форма записи начала вытеснять прежний знак R. Однако некоторое время знак корня писали разрывая верхнюю
- 48. Блиц опрос. Какие уравнения называются иррациональными? 2. Какой метод является основным при решении иррациональных уравнений? 3.
- 50. Скачать презентацию














































 Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Представление результатов измерений. Неопределённость в измерениях
Представление результатов измерений. Неопределённость в измерениях Ознайомлення з дією множення
Ознайомлення з дією множення Считаем до 10. Тренажёр 1 класс
Считаем до 10. Тренажёр 1 класс Презентация к уроку математики во 2 классе на тему Контрольная работа
Презентация к уроку математики во 2 классе на тему Контрольная работа Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Прибавить и вычесть 1.Веселое путешествие
Прибавить и вычесть 1.Веселое путешествие Віднімання натуральних чисел. Властивості віднімання
Віднімання натуральних чисел. Властивості віднімання Занимательный материал №3
Занимательный материал №3 Математические ребусы
Математические ребусы Устный счёт 4 класс
Устный счёт 4 класс презентация .по математике Единица времени. Час
презентация .по математике Единица времени. Час Решение задач
Решение задач Сложение и вычитание многочленов
Сложение и вычитание многочленов Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число.
Математика. 4 класс.Прием письменного деления многозначных чисел на однозначное число. Организация современного урока математики в условиях реализации ФГОС
Организация современного урока математики в условиях реализации ФГОС Презентация к уроку математике Присчитывание и отсчитывание по 1 по программе Гармония
Презентация к уроку математике Присчитывание и отсчитывание по 1 по программе Гармония Геометрические преобразования пространства
Геометрические преобразования пространства Все действия с десятичными дробями
Все действия с десятичными дробями Координатная плоскость
Координатная плоскость Анализ геометрической формы предмета
Анализ геометрической формы предмета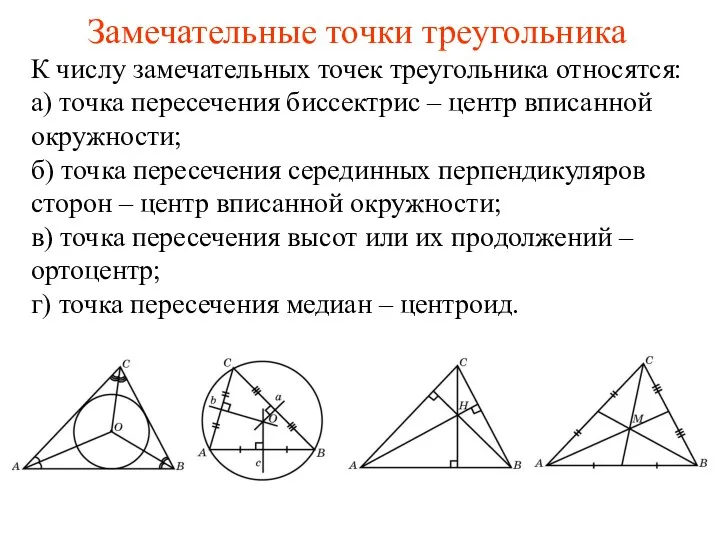 Замечательные точки в треугольнике
Замечательные точки в треугольнике Сложение и вычитание десятичных дробей. Урок 111
Сложение и вычитание десятичных дробей. Урок 111 Кратные и криволинейные интегралы
Кратные и криволинейные интегралы Сантиметр
Сантиметр Определенный интеграл как функция верхнего предела
Определенный интеграл как функция верхнего предела Среднее арифметическое
Среднее арифметическое Меры объема. Методика преподавания математики
Меры объема. Методика преподавания математики