Содержание
- 2. ////////////////// ////////////////// Числовые промежутки интервал a отрезок a ≤ x ≤ b [a;b] полуинтервал a ≤
- 3. 1. Определите, на каких рисунках изображены отрезки, а на каких – интервалы, и сделайте соответствующие записи
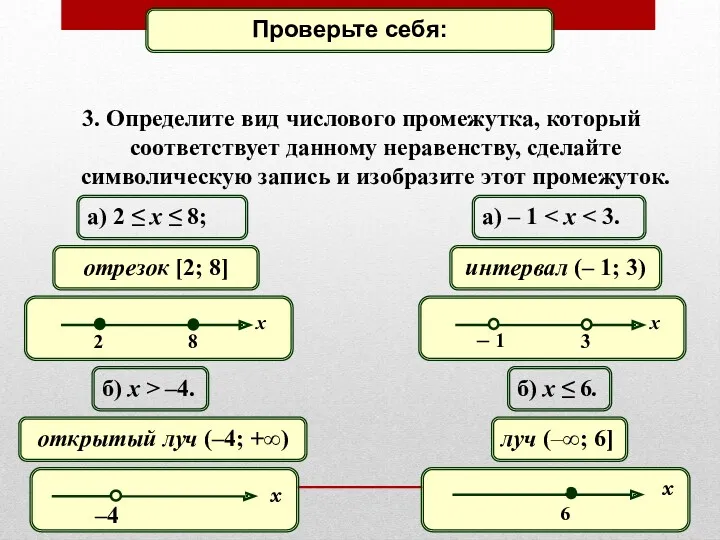
- 4. 3. Определите вид числового промежутка, который соответствует данному неравенству, сделайте символическую запись и изобразите этот промежуток.
- 5. Неравенство – это два числа или выражения, соединенные одним из знаков: > (больше), Линейное неравенство –
- 6. Правила решения линейных неравенств: Любой член неравенства можно перенести из одной части неравенства в другую с
- 7. Правила решения линейных неравенств 5х х - 4 x > 6
- 8. Решить неравенство 3х – 5 ≤ 7х – 15 перенесем слагаемое 7х в левую часть, а
- 9. 4 х Ответ: (4; + ∞)
- 11. Скачать презентацию







 Открытый урок математики во 2 классе. Тема Вычитание суммы из числа
Открытый урок математики во 2 классе. Тема Вычитание суммы из числа Модуль числа
Модуль числа Квадратные уравнения с параметром
Квадратные уравнения с параметром Деление дробей
Деление дробей Призма. Об’єм, площа поверхні призми
Призма. Об’єм, площа поверхні призми Математические задачки
Математические задачки Сложение рациональных чисел
Сложение рациональных чисел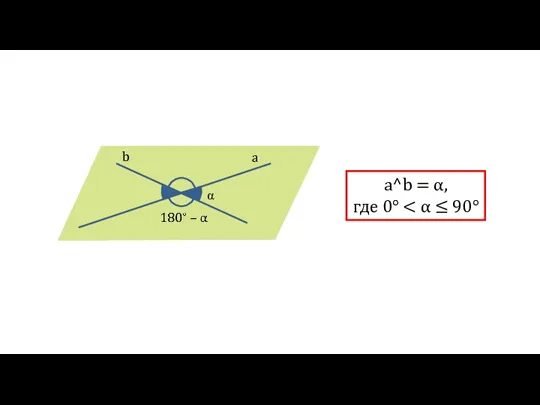 Перпендикулярные прямые
Перпендикулярные прямые Задачи по теме: Касательная к окружности
Задачи по теме: Касательная к окружности Старинные задачи по элементарной математике (Россия)
Старинные задачи по элементарной математике (Россия) Тригонометрические неравенства
Тригонометрические неравенства Отклик линейных систем. Свёртка
Отклик линейных систем. Свёртка Наука для детей. Книги
Наука для детей. Книги Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Действительные числа. 10 класс
Действительные числа. 10 класс Производная. Геометрический смысл производной. Возрастание и убывание
Производная. Геометрический смысл производной. Возрастание и убывание Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Применение систем нечеткой логики
Применение систем нечеткой логики Визначник другого та третього порядків. Алгебраїчні доповнення
Визначник другого та третього порядків. Алгебраїчні доповнення Дискретные и интервальные вариационные ряды
Дискретные и интервальные вариационные ряды Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Класифікація простих задач. Методичні основи роботи по розв'язуванню простих задач на додавання і віднімання
Класифікація простих задач. Методичні основи роботи по розв'язуванню простих задач на додавання і віднімання Умножение суммы на число
Умножение суммы на число урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск
урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск Сложение и вычитание десятичных дробей с одинаковым количеством знаков после запятой
Сложение и вычитание десятичных дробей с одинаковым количеством знаков после запятой Мир математики. Игра Счастливый случай
Мир математики. Игра Счастливый случай Зерттеу мәліметтерді негізгі статистикалық өңдеу әдістері
Зерттеу мәліметтерді негізгі статистикалық өңдеу әдістері Десятичные дроби и действия над ними
Десятичные дроби и действия над ними