Содержание
- 2. 2-е правило: |f(x)| = g(x) ⇔ 1-е правило: |f(x)| = g(x) ⇔ ЗАМЕЧАНИЕ. Фигурные скобки обозначают
- 3. Пример . Решить уравнение |x2 – x – 6| = |2x2 + x – 1|. Решение.
- 4. Третий способ освобождения от модуля – замена переменной Пример . Решить уравнение: Решение. Заметим, что ,
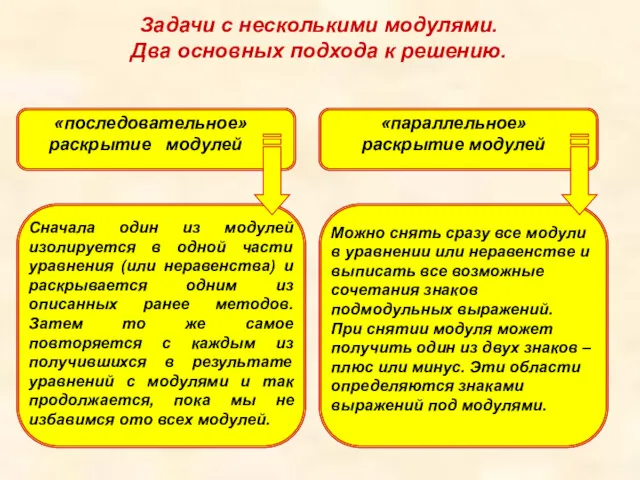
- 5. Задачи с несколькими модулями. Два основных подхода к решению. Сначала один из модулей изолируется в одной
- 6. Решение. Уединим второй модуль и раскроем его, пользуясь первым способом, то есть просто определением абсолютной величины:
- 7. Лишь первый и третий из этих корней удовлетворяют соответствующим неравенствам, а значит, и исходному уравнению. 2способ
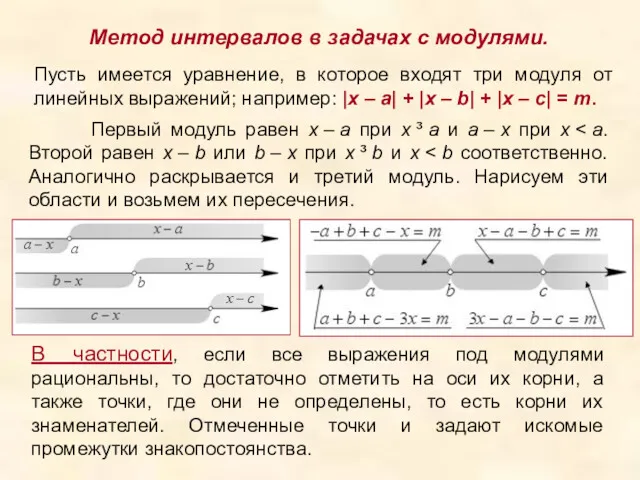
- 8. Метод интервалов в задачах с модулями. Пусть имеется уравнение, в которое входят три модуля от линейных
- 9. . Решение. Найдем нули функции x+2=0 или x+3=0 , откуда x=-2 , x=-3. Рассмотрим 3 возможных
- 10. Вложенные модули Последовательное раскрытие модулей наиболее эффективно в "задачах-матрешках", где внутри одного модуля находится другой, а
- 11. Модули и квадраты Он основан на двух очевидных соображениях. Во-первых, из двух неотрицательных чисел то больше,
- 12. Модули неотрицательных выражений. Решение. Нетрудно догадаться, что все выражения, стоящие под знаком второго, третьего и т.д.
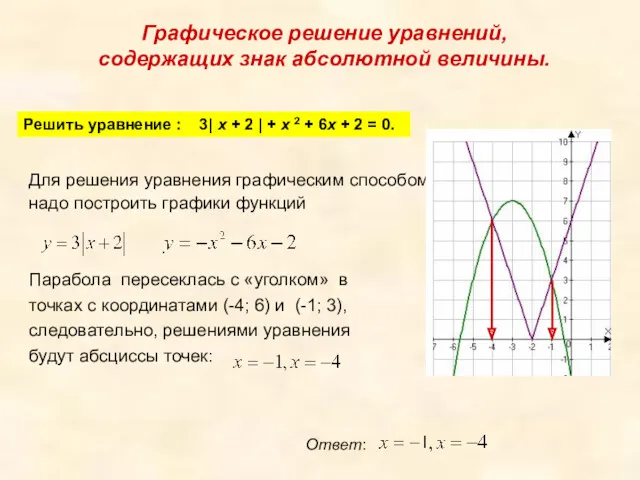
- 13. Графическое решение уравнений, содержащих знак абсолютной величины. Решить уравнение : 3| x + 2 | +
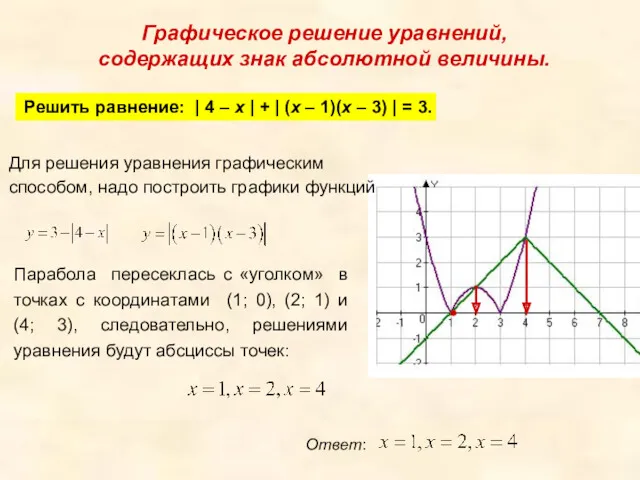
- 14. Графическое решение уравнений, содержащих знак абсолютной величины. Решить равнение: | 4 – x | + |
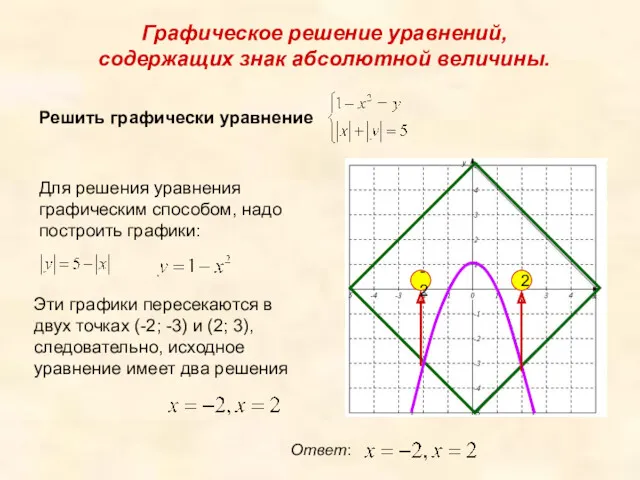
- 15. Графическое решение уравнений, содержащих знак абсолютной величины. Решить графически уравнение
- 17. Скачать презентацию









 Округление натуральных чисел. Повторение изученного
Округление натуральных чисел. Повторение изученного Общий приём сложения однозначных чисел с переходом через десяток
Общий приём сложения однозначных чисел с переходом через десяток Экстремум функции двух переменных (пример 2)
Экстремум функции двух переменных (пример 2) Повторення вивченого. Робота з малюнками й текстами (урок № 137)
Повторення вивченого. Робота з малюнками й текстами (урок № 137)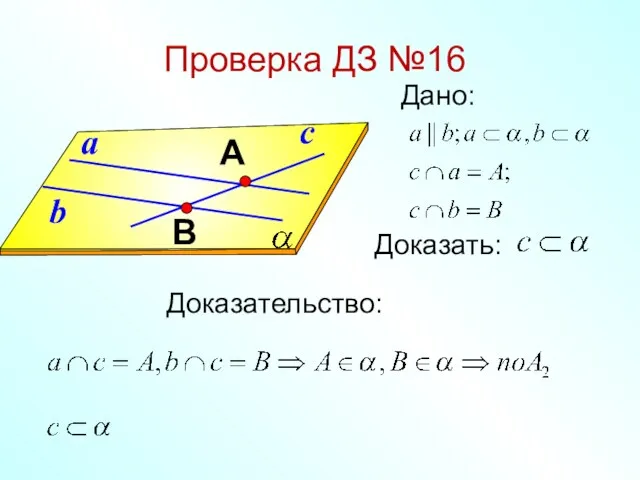 Параллельность прямой и плоскости
Параллельность прямой и плоскости Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2 Интеграл. Формула Ньютона – Лейбница
Интеграл. Формула Ньютона – Лейбница Урок Угол. Виды углов 2 класс
Урок Угол. Виды углов 2 класс Разметка прямоугольника с помощью угольника
Разметка прямоугольника с помощью угольника В гости к Бабе Яге Счёт до 10
В гости к Бабе Яге Счёт до 10 Решение задач с помощью уравнений
Решение задач с помощью уравнений Дискретне перетворення Фур’є. Лекція 2
Дискретне перетворення Фур’є. Лекція 2 Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей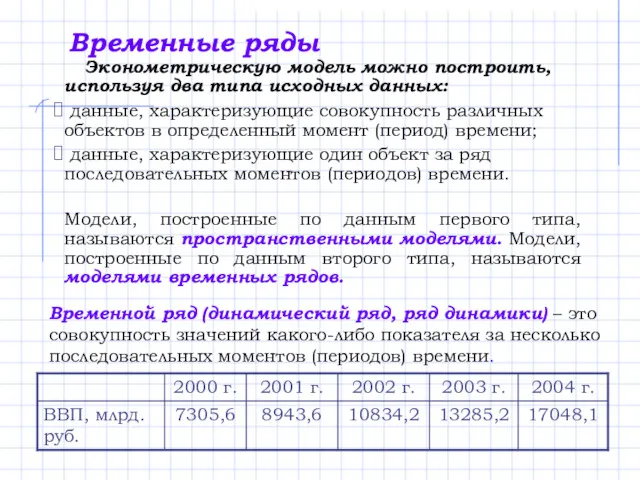 Временные ряды
Временные ряды ЕГЭ. Текстовые задачи. Теория вероятностей. (Лекция 1)
ЕГЭ. Текстовые задачи. Теория вероятностей. (Лекция 1) Десятичные дроби
Десятичные дроби Учимся решать задачи на смеси, растворы и сплавы
Учимся решать задачи на смеси, растворы и сплавы Умножение. Табличные случаи умножения числа 9. (математика, 2 класс. УМК Гармония).
Умножение. Табличные случаи умножения числа 9. (математика, 2 класс. УМК Гармония). Математика в юриспруденции
Математика в юриспруденции Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ
Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Арифметические действия (повторение)
Арифметические действия (повторение) Отношения и предикаты. (Лекция 7)
Отношения и предикаты. (Лекция 7) Аналіз зв’язку між змінними: кореляція і регресія
Аналіз зв’язку між змінними: кореляція і регресія Комплексные числа
Комплексные числа Формирование метапредметных результатов на уроках математики. Классификация задач с практическим содержанием
Формирование метапредметных результатов на уроках математики. Классификация задач с практическим содержанием Презентация Состав чисел первого десятка
Презентация Состав чисел первого десятка Знатоки математики. Конкурс эрудитов в начальной школе
Знатоки математики. Конкурс эрудитов в начальной школе