ВСПОМНИМ…
Граф
Простейшая модель системы.Отображает элементарный состав системы и структуру связей
Сеть
Граф с возможностью
множества различных путей перемещения по ребрам между некоторыми парами вершин
Граф называется связным
если любая пара его вершин — связная.
Ребро соединяет две вершины графа
элемент (точка) графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом
Вершина
Ребро
это ориентированное ребро.
Дуга
ребро, начало и конец которого находятся в одной и той же вершине
Петля
любой связный граф, не имеющий циклов.
Дерево



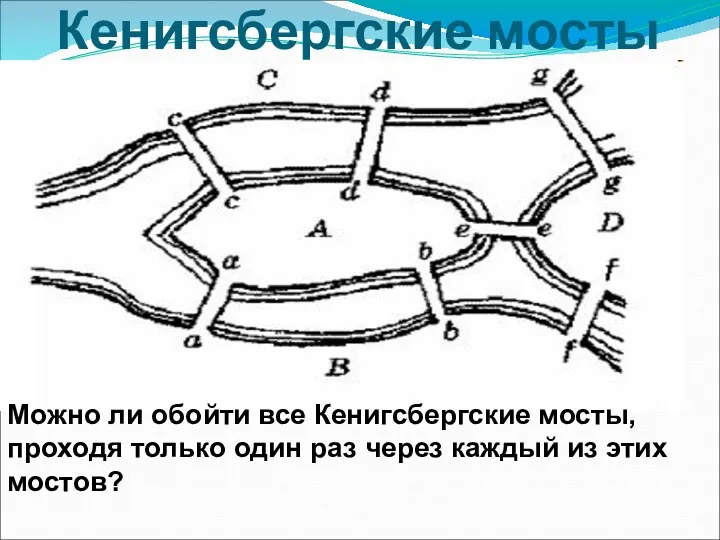
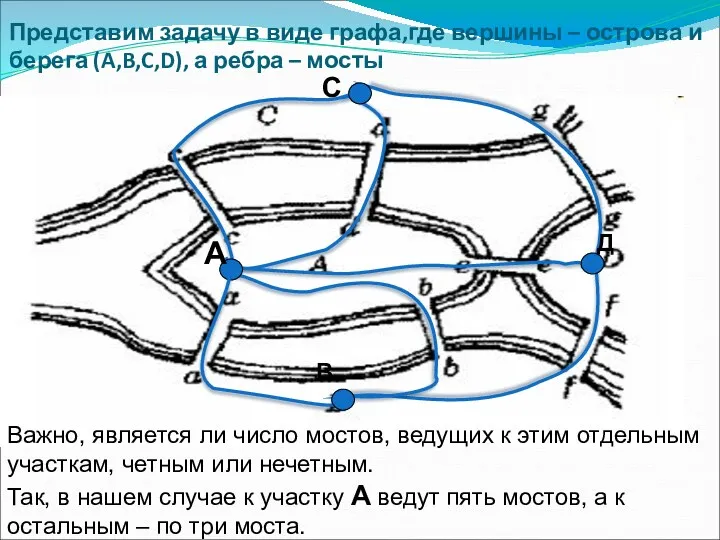
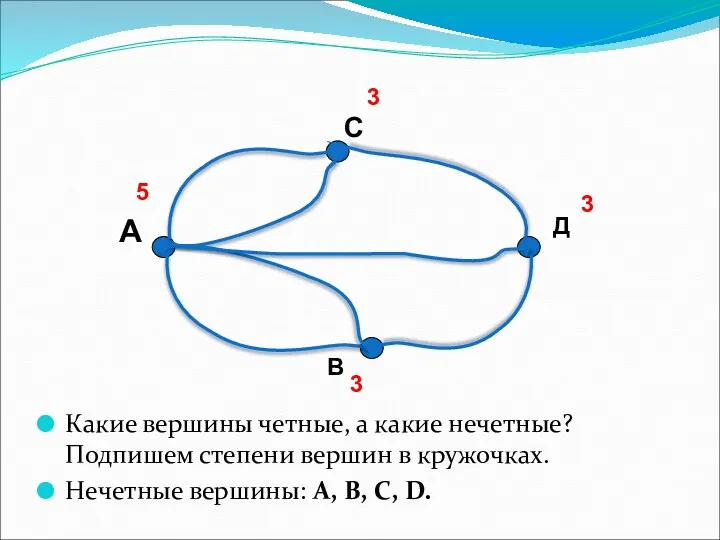


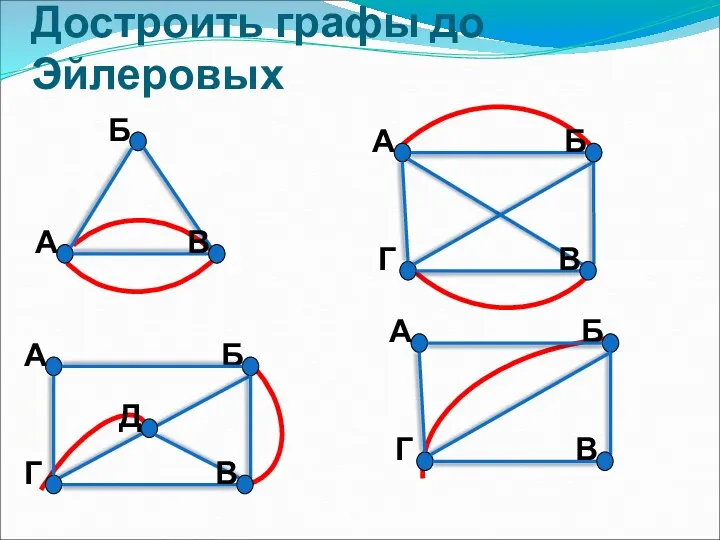
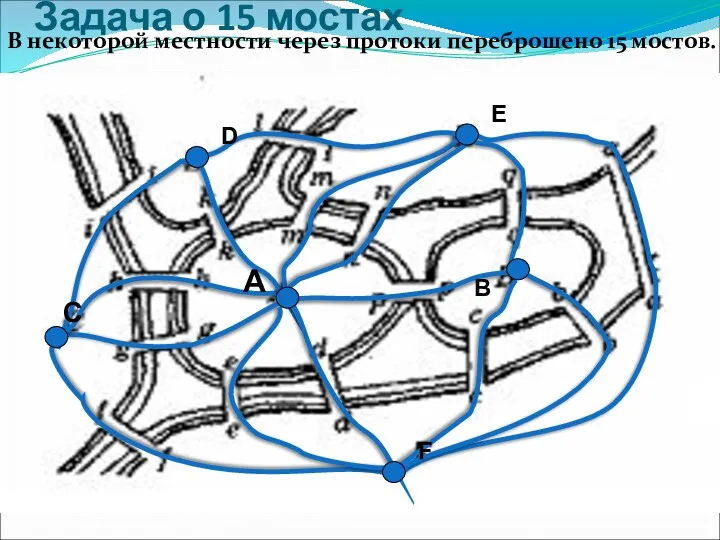
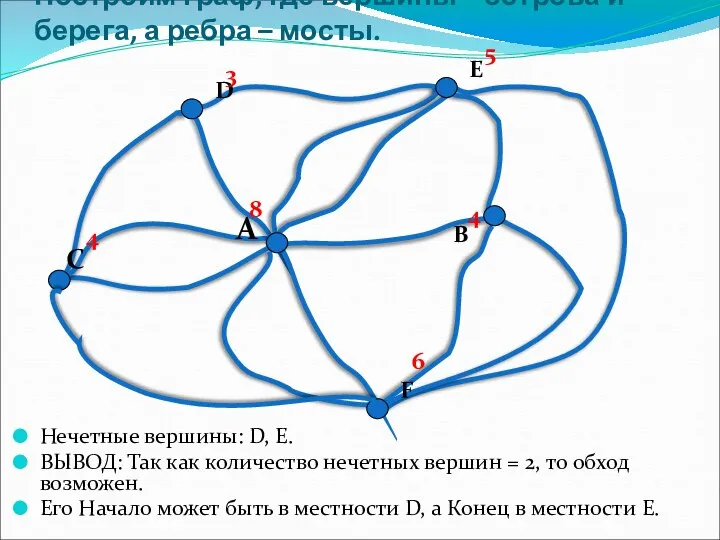
 Взаимосвязь компонентов и результатов действия сложения и вычитания
Взаимосвязь компонентов и результатов действия сложения и вычитания Моделирование систем. Классификация моделей
Моделирование систем. Классификация моделей Презентация к уроку математики Решение задач
Презентация к уроку математики Решение задач Контрольная работа по математике 4 класс
Контрольная работа по математике 4 класс Единицы массы. Грамм
Единицы массы. Грамм Работа с текстовой математической задачей
Работа с текстовой математической задачей Задачи на расстояние
Задачи на расстояние Правильные многоугольники
Правильные многоугольники Презентация урока-сказки на тему Решение задач
Презентация урока-сказки на тему Решение задач урок по программе Школа России 4 класс. Задачи на движение. Закрепление
урок по программе Школа России 4 класс. Задачи на движение. Закрепление Подготовка к ЕГЭ – 2014 по математике. Подробное решение задачи С2
Подготовка к ЕГЭ – 2014 по математике. Подробное решение задачи С2 Презентации к 3м урокам математики
Презентации к 3м урокам математики презентация Космическое путешествие
презентация Космическое путешествие Статистика и теория вероятностей. 9 класс
Статистика и теория вероятностей. 9 класс Числа от 11 до 20
Числа от 11 до 20 Графическое решений квадратных уравнений
Графическое решений квадратных уравнений презентация по ФМЭП Играем с Машей и медведем
презентация по ФМЭП Играем с Машей и медведем Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов Арифметическая прогрессия
Арифметическая прогрессия Математичні моделі міжгалузевого балансу Леонтьєва
Математичні моделі міжгалузевого балансу Леонтьєва Цилиндр. Основные сведения
Цилиндр. Основные сведения Решаем задачи на умножение и деление
Решаем задачи на умножение и деление Центральные и вписанные углы
Центральные и вписанные углы Ch8: Hypothesis Testing (2 Samples)
Ch8: Hypothesis Testing (2 Samples) Величина. Методика изучения Объема
Величина. Методика изучения Объема Таблица умножения. Тренажер
Таблица умножения. Тренажер Сравнение отрезков и углов
Сравнение отрезков и углов Большая математическая мастерская
Большая математическая мастерская