Содержание
- 2. Открытие логарифма Определение логарифма Свойства логарифмов Дополнительные формулы Свойства логарифмической функции График функции Решение логарифмических уравнений
- 3. История логарифма началась в 17 веке. Логарифмы были изобретены шотландским дворянином Джоном Непером (1550-1617),опубликовавшим свои работы
- 4. Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить
- 5. При любом a > 0 (a = 1) и любых положительных x и y: loga 1
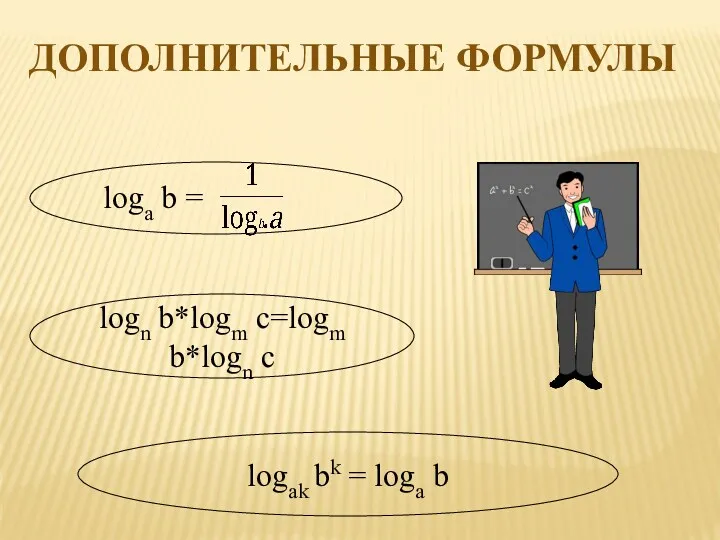
- 6. loga b = logn b*logm c=logm b*logn c logak bk = loga b ДОПОЛНИТЕЛЬНЫЕ ФОРМУЛЫ
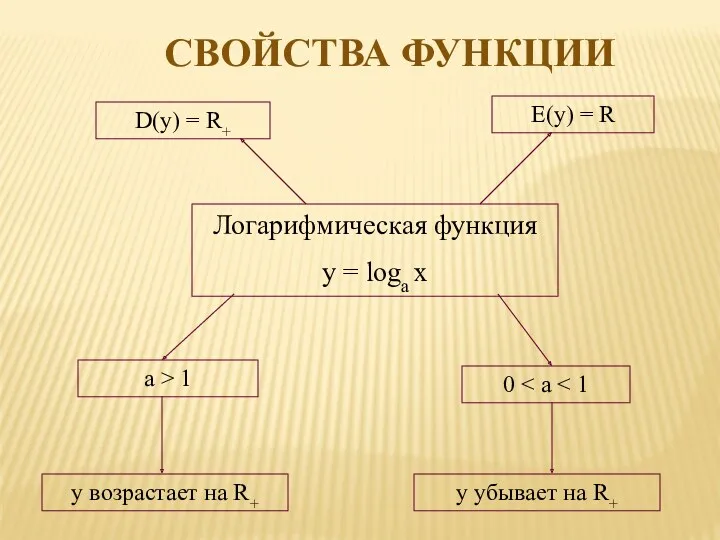
- 7. Логарифмическая функция y = loga x D(y) = R+ E(y) = R a > 1 0
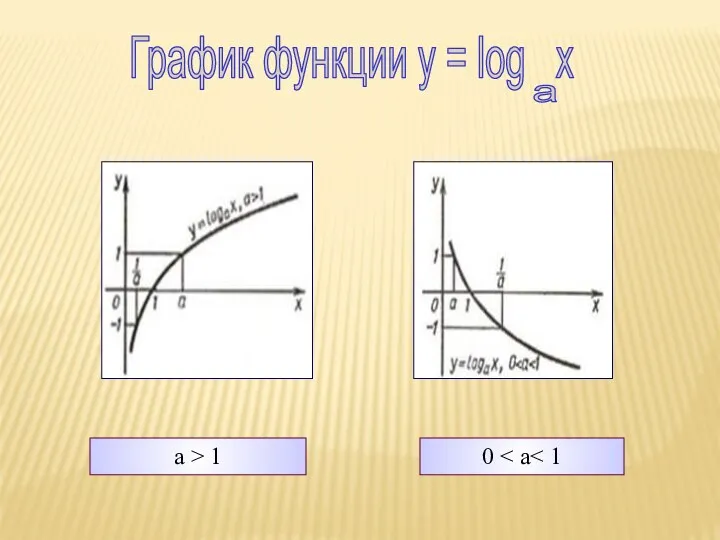
- 8. a > 1 0
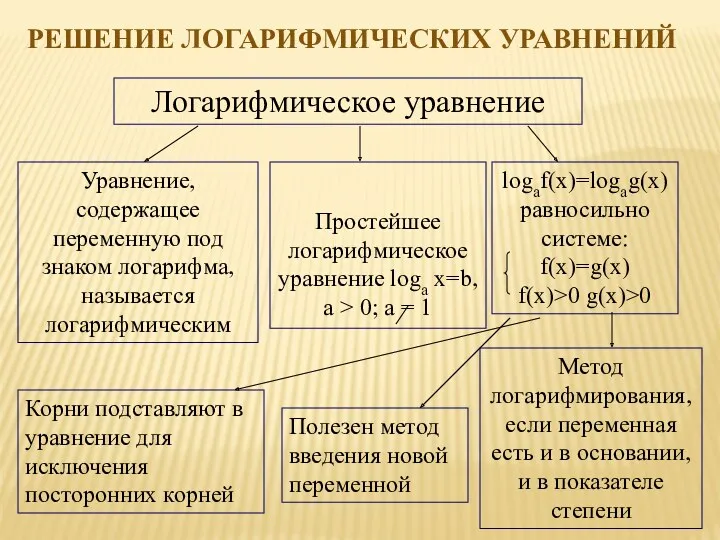
- 9. Логарифмическое уравнение Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим Простейшее логарифмическое уравнение loga x=b, a
- 10. xlog2x+2=8 Прологарифмируем обе части уравнения по основанию 2: log2(xlog2x+2)=log28, (log2x+2)*log2x=3. Пусть log2x=y, тогда y2+ 2y -
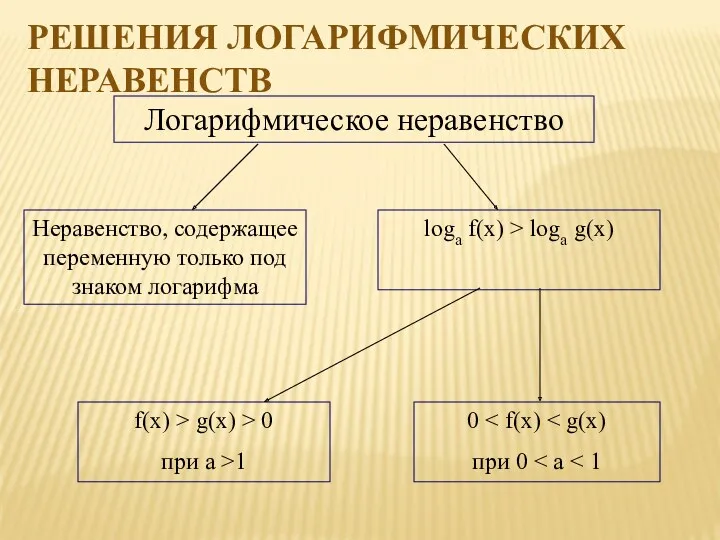
- 11. Логарифмическое неравенство Неравенство, содержащее переменную только под знаком логарифма loga f(x) > loga g(x) f(x) >
- 13. Скачать презентацию





 Комплексные числа
Комплексные числа Презентация Задачи осени. Диск
Презентация Задачи осени. Диск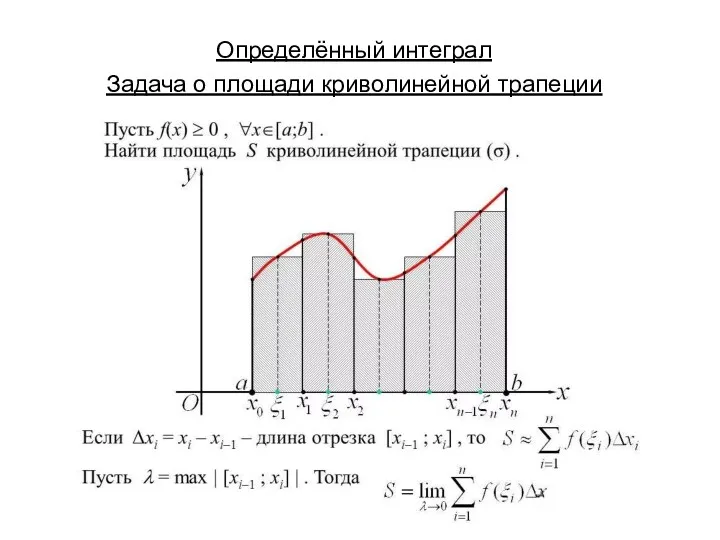 Определённый интеграл. Задача о площади криволинейной трапеции
Определённый интеграл. Задача о площади криволинейной трапеции Треугольник. Виды треугольников
Треугольник. Виды треугольников Узоры и орнаменты на посуде. Проект по математике
Узоры и орнаменты на посуде. Проект по математике Совместные действия с десятичными дробями. 6 класс
Совместные действия с десятичными дробями. 6 класс Основные понятия и определения теории нечетких множеств
Основные понятия и определения теории нечетких множеств Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Тест Умножение и деление на 7
Тест Умножение и деление на 7 Наименьшее общее кратное
Наименьшее общее кратное Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива
Урок математики в 1 классе по теме: Число и цифра 7 УМК Перспектива Итоговый тест по математике, 1 класс
Итоговый тест по математике, 1 класс Цифра ноль
Цифра ноль Математический кроссворд
Математический кроссворд Основное свойство дробей
Основное свойство дробей Антагонистические игры
Антагонистические игры Четыре периода развития математики
Четыре периода развития математики Треугольник и его элементы
Треугольник и его элементы КВН Умники и умницы
КВН Умники и умницы Объем шара
Объем шара Графический способ решения уравнений. Урок 95
Графический способ решения уравнений. Урок 95 Моя страничка на proshkolu.ru
Моя страничка на proshkolu.ru Основы стандартизации, сертификации и метрологии
Основы стандартизации, сертификации и метрологии Преобразование выражений при решений уравнений
Преобразование выражений при решений уравнений Сравнение дробей. Классная работа
Сравнение дробей. Классная работа Иррациональные уравнения
Иррациональные уравнения Презентация урока математики Закрепление пройденного материала 1 класс Школа России
Презентация урока математики Закрепление пройденного материала 1 класс Школа России