Содержание
- 2. Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств
- 3. Основные определения
- 6. Пример 1: Формализуем неточное определение "горячий чай". В качестве x (область рассуждений) будет выступать шкала температуры
- 7. Пример2: Пусть множество U есть множество действительных чисел. Нечеткое множество A, обозначающее множество чисел, близких к
- 8. Нечеткое множество А называется пустым, если µA(u) =0, ∀ u ∈ U. В любом данном множестве
- 9. Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном
- 10. Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов,
- 11. Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций: Минимаксные: Алгебраические:
- 12. Графическая интерпретация логических операций: а — нечеткое множество А; б — нечеткое множество Ā; в —
- 13. Носителем нечеткого множества А называется обычное подмножество таких точек U, для которых величина µА(u) положительна. Носитель
- 14. Нечеткое множество называется нормальным, если В противном случае оно называется субнормальным. Непустое субнормальное нечеткое множество можно
- 15. Элементы множества U, для которых степень принадлежности µА(u) = 0.5 называются точками перехода нечеткого множества А.
- 16. Множество α-уровня называют сечением (срезом) α нечеткого множества А. Если µА(u) ≥ α, то говорят о
- 17. Нечеткое подмножество универсального множества U может быть подмножеством другого нечеткого или обычного (четкого) подмножества (то есть
- 18. Пример 3: Пусть U = {-8, -5, -3, 0, 1, 2, 4, 6, 9} – множество
- 19. Пример 4: Если универсальное множество U = {a, b, c, d}, а определенные на нем нечеткие
- 20. Пример 5: Если нечеткое множество А = {0.3/a, 0.4/d, 0.7/c, 0.8/f, 0.6/b}, то множеством α-уровня при
- 21. Пример 6: Пусть универсальное множество U представлено в виде {a, b, c, d, e} и нечеткое
- 22. Нечеткие отношения Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется
- 23. Отношением R на множестве X называется некоторое подмножество декартова произведения X×X. В соответствии с этим определением
- 25. 2) графовой
- 26. Свойства четких отношений
- 27. Нечеткие отношения
- 29. Операции над нечеткими отношениями Пусть на множестве U1×U2 заданы два нечетких отношения A и B с
- 30. Пример:
- 31. Нечеткое отношение B включает в себя (или содержит) нечеткое отношение A (A ⊂ B), если для
- 32. Обычное подмножество α-уровня нечеткого отношения. Пусть α∈[0,1]. Обычным подмножеством α-уровня нечеткого отношения R⊂Χ×Χ называется обычное подмножество
- 33. Пример:
- 34. Первая проекция нечеткого отношения R определяется функцией принадлежности µR(1) (x) =maxµR(x, y). Аналогично вторая проекция: µR(2)
- 35. Пример: Вычислим первую, вторую и глобальную проекции отношения R, заданного матрицей:
- 36. Важное значение в теории нечетких множеств имеет композиция (или произведение) нечетких отношений. В отличие от обычных
- 37. Свойства нечетких отношений Рефлексивность. (например, отношения «у примерно равно x», «y близко x» являются рефлексивными) Антирефлексивность.
- 38. Специальные типы нечетких отношений Нечеткие отношения предпорядка Нечеткие отношения порядка Отношение подобия, или нечеткое отношение эквивалентности
- 39. Классы нечетких отношений Все типы нечетких отношений в зависимости от свойств, которыми они обладают, могут быть
- 40. Рефлексивные и симметричные отношения обычно называют отношениями сходства (толерантности, безразличия или неразличимости). Эти отношения обозначаются буквой
- 41. Антисимметричные отношения, называемые предпорядками и обозначаемые буквой P. В зависимости от выполнения условия рефлексивности или антирефлексивности
- 42. На следующем уровне классификации из каждого класса отношений могут быть выделены отношения специального вида. Определяющим условием
- 43. Показатель размытости нечетких множеств Нечеткие множества используются для описания плохо определенных, неоднозначно понимаемых ситуаций, объектов, понятий.
- 44. Существует несколько аспектов, связанных с понятием показателя размытости нечеткого множества. Прежде всего, это — интерпретация показателя
- 46. Эта двусмысленность объекта x по отношению к свойству A максимальна, когда степени принадлежности объекта к обоим
- 47. Выбор конкретного показателя зависит от условий задачи. Необходимо обратить также внимание на связь между показателем размытости
- 48. Нечеткие меры При решении многих задач анализа сложных систем в условиях неопределенности широко используются методы теории
- 49. Один из возможных подходов может основываться на обобщении понятия меры и построении нечетких мер, свободных от
- 50. Под субъективной вероятностной мерой понимается степень уверенности в данном событии, возникающая у человека на основе известных
- 51. Субъективную вероятность можно рассматривать как индивидуальный способ обработки тех аспектов субъективных данных, которые доступны индивидуальному суждению.
- 53. Скачать презентацию
 Геометрические фигуры: круг, треугольник, квадрат
Геометрические фигуры: круг, треугольник, квадрат Различные способы умножения. Проектная работа
Различные способы умножения. Проектная работа Математическая сказка Теремок
Математическая сказка Теремок Свойства площадей геометрических фигур
Свойства площадей геометрических фигур признаки делимости на 10, на 5, на 2
признаки делимости на 10, на 5, на 2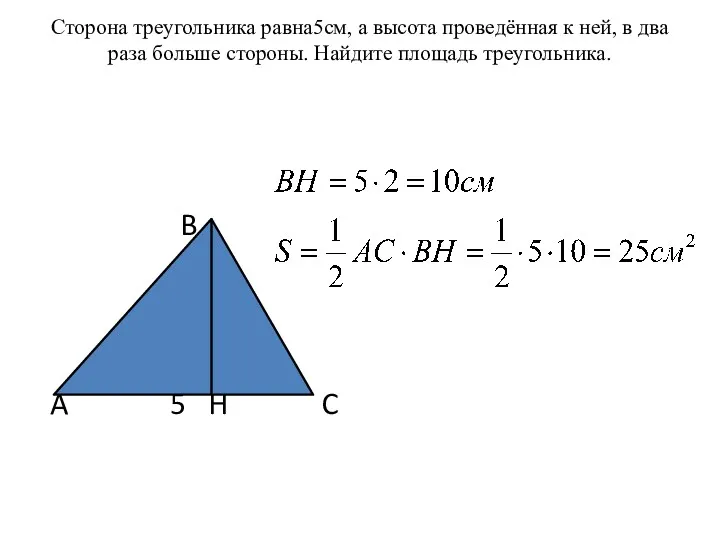 Решение задач. Площадь треугольника
Решение задач. Площадь треугольника Деление многозначных чисел на двузначное число
Деление многозначных чисел на двузначное число Оригами
Оригами Математическая викторина. Своя игра
Математическая викторина. Своя игра Раскрытие скобок. Математика. 6 класс
Раскрытие скобок. Математика. 6 класс Виды простых задач. 1 класс
Виды простых задач. 1 класс Устный счет. 5 класс
Устный счет. 5 класс Задача 6 стр.103
Задача 6 стр.103 Уравнение прямой. 9 класс
Уравнение прямой. 9 класс Математика в стихах. 5 класс
Математика в стихах. 5 класс Уравнения и неравенства с параметрами
Уравнения и неравенства с параметрами Логарифмы. Зачем они нужны. Джон Не́пер
Логарифмы. Зачем они нужны. Джон Не́пер Пропорции и отношения
Пропорции и отношения Правильні многокутники
Правильні многокутники Параллельные прямые
Параллельные прямые Формулы сокращённого умножения. Урок обобщения знаний
Формулы сокращённого умножения. Урок обобщения знаний Нумерация_1000
Нумерация_1000 Показательная и логарифмическая функции. Показательные неравенства
Показательная и логарифмическая функции. Показательные неравенства Презентация к уроку математики в 1 классе по теме:Прибавить и вычесть 1. УМК ШР
Презентация к уроку математики в 1 классе по теме:Прибавить и вычесть 1. УМК ШР Математика в играх и задачах
Математика в играх и задачах Задачи, приводящие к теории графов. Основные понятия и определения. (Лекция 13)
Задачи, приводящие к теории графов. Основные понятия и определения. (Лекция 13) Екі векторды векторлық көбейту
Екі векторды векторлық көбейту Синтез комбинационных схем. Типовые логические элементы и их обозначения на функциональных схемах
Синтез комбинационных схем. Типовые логические элементы и их обозначения на функциональных схемах