Содержание
- 2. Системы случайных величин. (Краткое напоминание) Совокупность двух случайных величин {X,Y}, определенных на одном и том же
- 3. Функция распределения Функцией распределения F(x,y) системы двух случайных величин {X,Y} называется вероятность совместного выполнения двух событий:
- 4. Дискретным случайным вектором называется такой случайный вектор, который может принимать значения только из заранее известной таблицы
- 5. Условные обозначения: СВ – случайная величина. НСВ - непрерывная случайная величина. ДСВ – дискретная случайная величина.
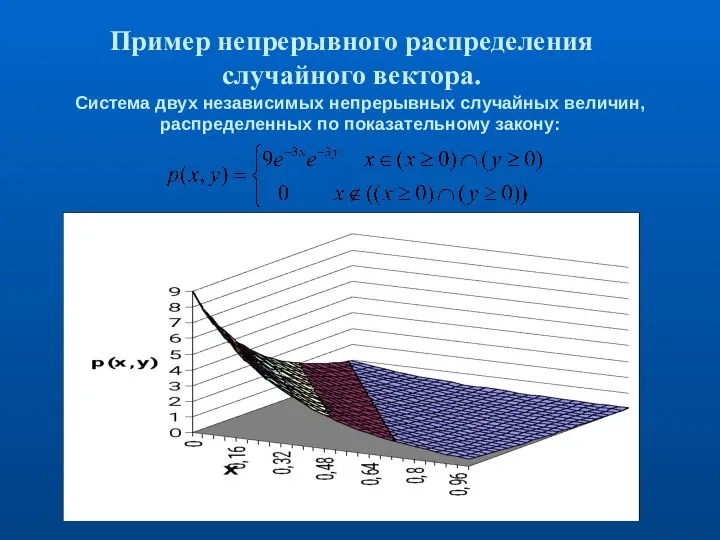
- 6. Пример непрерывного распределения случайного вектора. Система двух независимых непрерывных случайных величин, распределенных по показательному закону:
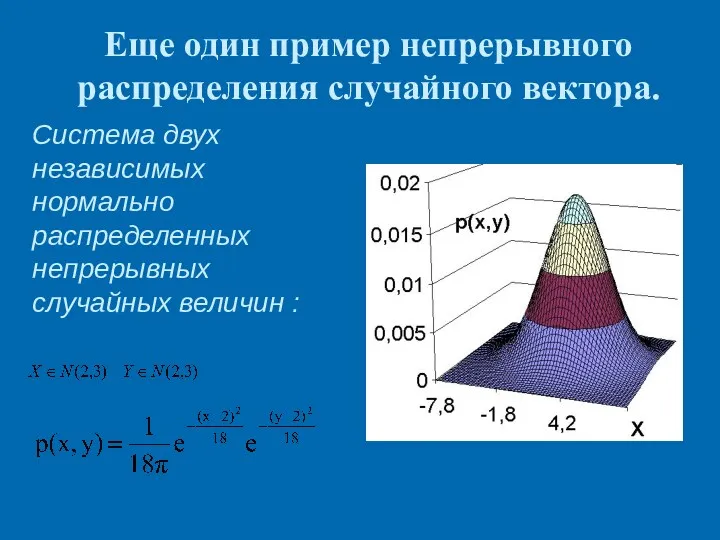
- 7. Еще один пример непрерывного распределения случайного вектора. Система двух независимых нормально распределенных непрерывных случайных величин :
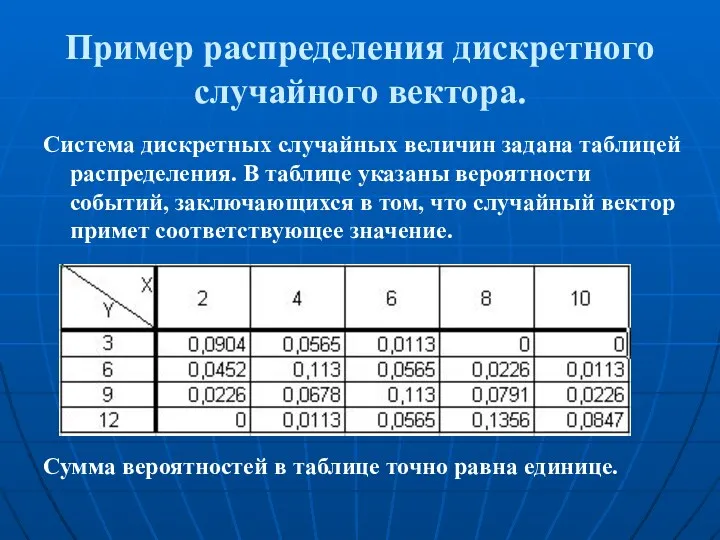
- 8. Пример распределения дискретного случайного вектора. Система дискретных случайных величин задана таблицей распределения. В таблице указаны вероятности
- 9. Функции F1(x)=F(x,+∞) и F2(x)=F(+∞,y) называются частными (маргинальными) функциями распределения составляющих систему случайных величин. Для систем непрерывных
- 10. Имеют место следующие равенства: p(x,y)=py(x)p2(y) p(x,y)=px(y)p1(y)
- 11. Зависимость и независимость случайных величин, входящих в состав систем случайных величин. Две случайные величины, входящие в
- 12. Зависимость и независимость случайных величин, входящих в состав систем случайных величин (продолжение) Теорема: Для того, чтобы
- 13. Числовые характеристики систем случайных величин. Ковариация и коэффициент корреляции. Ковариацией cov(X,Y) (или Kxy) двух случайных величин
- 14. Для систем дискретных случайных величин имеют место формулы: Здесь суммирование ведется по всем «клеткам» таблицы распределения.
- 15. Коэффициентом корреляции r(X.Y) двух случайных величин называется величина Если ковариация равна нулю, то X и Y
- 16. Регрессия. Условным математическим ожиданием случайной величины Y - ExY называется ее математическое ожидание, вычисленное по условному
- 17. Регрессия (продолжение). Условное математическое ожидание случайной величины Y - ExY при заданном значении x называется регрессией
- 19. Скачать презентацию













 Линейное программирование. Задачи
Линейное программирование. Задачи Решение линейных уравнений. 6 класс
Решение линейных уравнений. 6 класс Преобразование суммы тригонометрических функций в произведение и произведение в сумму
Преобразование суммы тригонометрических функций в произведение и произведение в сумму Квадратные неравенства
Квадратные неравенства Векторы в пространстве
Векторы в пространстве Вычитание вида 11-
Вычитание вида 11- Застосування похідної
Застосування похідної Делимость произведения. Урок 99
Делимость произведения. Урок 99 Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур
Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур Тренажёр Кого сфотографировал Шарик?
Тренажёр Кого сфотографировал Шарик? Занятие по математике в средней группе по теме: Геометрические фигуры
Занятие по математике в средней группе по теме: Геометрические фигуры Отношения a : b
Отношения a : b Аксиома параллельных прямых
Аксиома параллельных прямых Графический способ решения систем уравнений
Графический способ решения систем уравнений Аксиомы стереометрии
Аксиомы стереометрии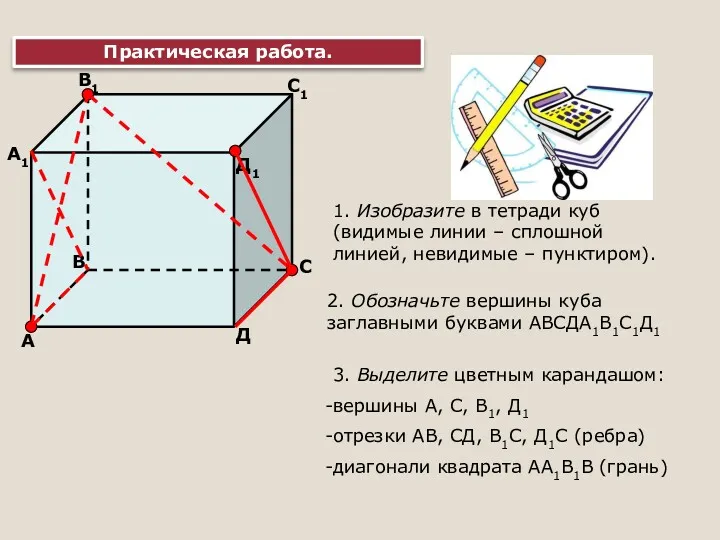 Решение задач по стереометрии
Решение задач по стереометрии Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Геометрия. Решаем задачи. 8 класс
Геометрия. Решаем задачи. 8 класс Деление дробей. Задание для устного счета. Упражнение 14. 6 класс
Деление дробей. Задание для устного счета. Упражнение 14. 6 класс Математическое моделирование химико-технологических процессов
Математическое моделирование химико-технологических процессов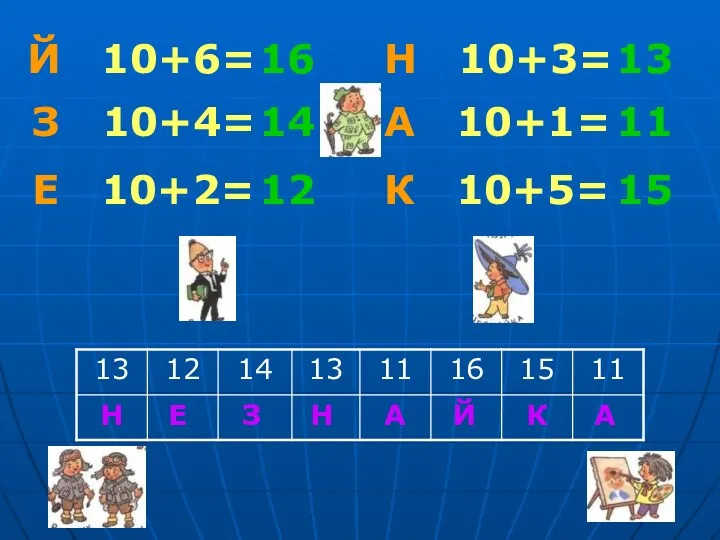 устный счет, переход через десяток
устный счет, переход через десяток Моделирование текстовых задач как метод формирования познавательных УУД
Моделирование текстовых задач как метод формирования познавательных УУД Устный счёт
Устный счёт Приключение колобка НОД Познание (математика) 2-я младшая группа
Приключение колобка НОД Познание (математика) 2-я младшая группа Презентация к уроку математики по теме Единица измерения длины - сантиметр (УМК Школа России)
Презентация к уроку математики по теме Единица измерения длины - сантиметр (УМК Школа России) Нумерация чисел в пределах 10. (1 класс)
Нумерация чисел в пределах 10. (1 класс) Удивительная цифра два
Удивительная цифра два Корреляционный анализ
Корреляционный анализ