Случайная величина. Закон распределения случайной величины. Числовые характеристики случайной величины презентация
Содержание
- 2. Случайная величина
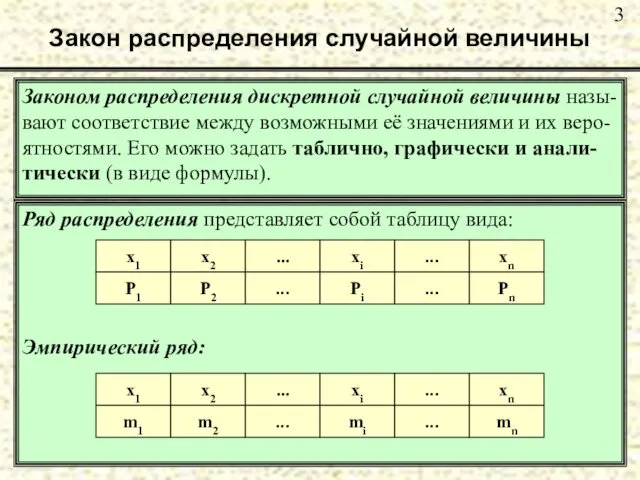
- 3. Закон распределения случайной величины
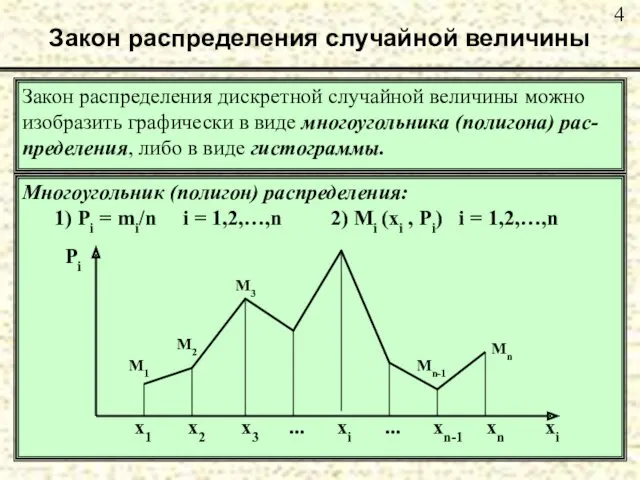
- 4. Закон распределения случайной величины Закон распределения дискретной случайной величины можно изобразить графически в виде многоугольника (полигона)
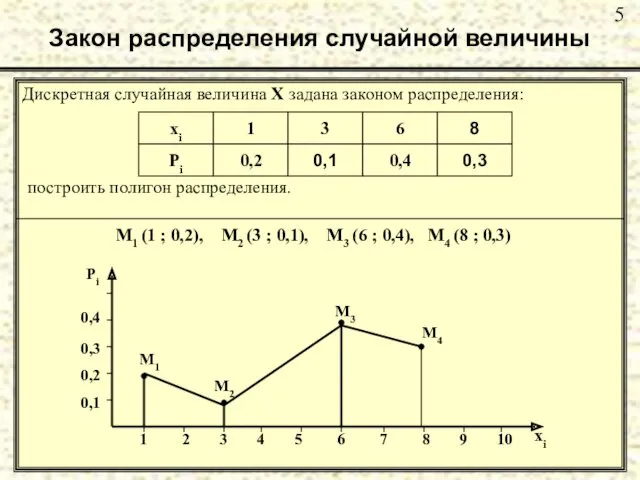
- 5. Закон распределения случайной величины Дискретная случайная величина Х задана законом распределения: построить полигон распределения. M1 (1
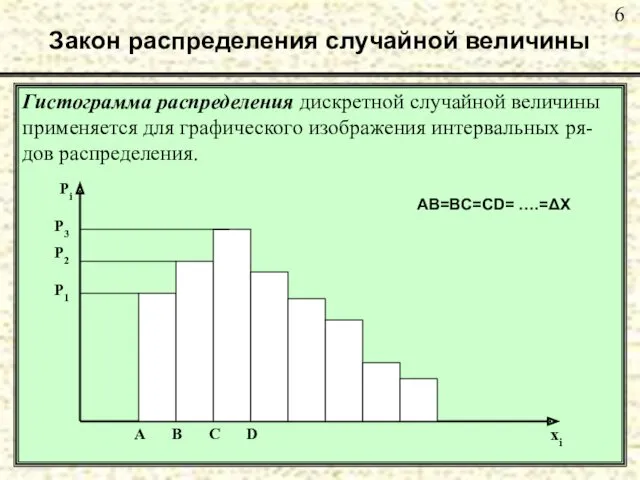
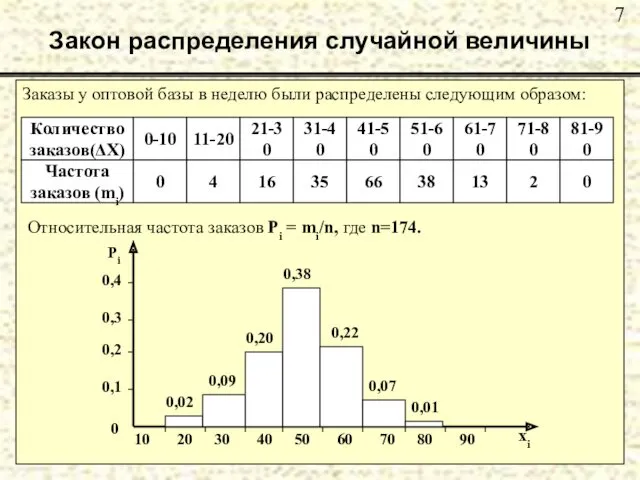
- 6. Закон распределения случайной величины Гистограмма распределения дискретной случайной величины применяется для графического изображения интервальных ря- дов
- 7. Закон распределения случайной величины
- 8. Закон распределения случайной величины Функций распределения случайной величины на сегодняшний день выявлено несколько десятков, но практически
- 9. Биномиальное распределение Биномиальное распределение - это распределение случайных величин, в котором может быть только два исхода:
- 10. Распределение Пуассона Распределение Пуассона - это распределение числа появления редких случайных событий, которые могут принимать только
- 11. Распределение Пуассона С помощью формулы Пуассона можно найти вероятность появ- ления однородных событий, следующих друг за
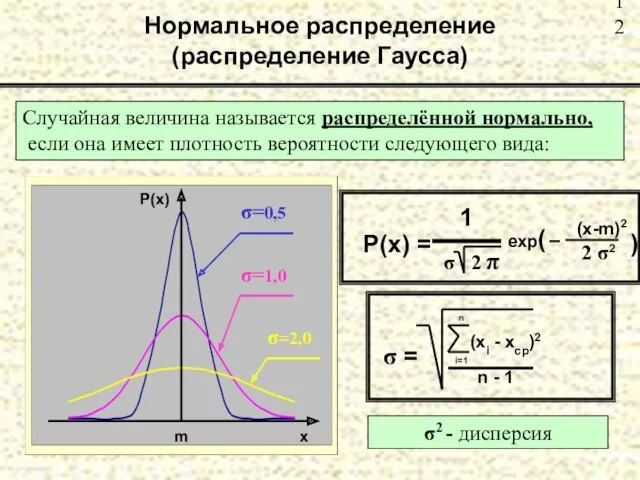
- 12. Нормальное распределение (распределение Гаусса) Случайная величина называется распределённой нормально, если она имеет плотность вероятности следующего вида:
- 14. Скачать презентацию





 Таблиця множення числа 4
Таблиця множення числа 4 Скільки сотень у числі? Підготовчі вправи
Скільки сотень у числі? Підготовчі вправи Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Дифференцируемость функции нескольких переменных. Лекция 3
Дифференцируемость функции нескольких переменных. Лекция 3 Табличное сложение и вычитание
Табличное сложение и вычитание Умножение и деление
Умножение и деление Функции y = tgx и y = ctgx, их свойства и графики
Функции y = tgx и y = ctgx, их свойства и графики Задачи Модуля Геометрия
Задачи Модуля Геометрия Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли
Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Решение задач по теме Четырехугольники по готовым чертежам
Решение задач по теме Четырехугольники по готовым чертежам Умножение числа 2 (2 класс)
Умножение числа 2 (2 класс) Електронний альбом дидактичних матеріалів. Аналітична геометрія у просторі. (Частина 2)
Електронний альбом дидактичних матеріалів. Аналітична геометрія у просторі. (Частина 2) Kristālisko vielu ārējā (formas) simetrija
Kristālisko vielu ārējā (formas) simetrija Определение подобных треугольников. Задания для устного счета. Упражнение 9. 8 класс
Определение подобных треугольников. Задания для устного счета. Упражнение 9. 8 класс Математическое ожидание случайной величины
Математическое ожидание случайной величины Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Сложение чисел с разными знаками
Сложение чисел с разными знаками Золотое сечение
Золотое сечение Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Квадратное неравенство
Квадратное неравенство Лист Мёбиуса
Лист Мёбиуса Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Основы формальной логики
Основы формальной логики Матрицы, операции над матрицами, теорема существования обратной матрицы. Лекция 3
Матрицы, операции над матрицами, теорема существования обратной матрицы. Лекция 3 Применение ИКТ на уроках математики, как средство формирования УУД у школьников
Применение ИКТ на уроках математики, как средство формирования УУД у школьников Формирование элементарных математических представлений в игровой деятельности
Формирование элементарных математических представлений в игровой деятельности