Содержание
- 2. Generating functions Generating functions provide a powerful tool for solving LHRRWCCs, as will be seen shortly.
- 3. Generating functions Abraham De Moivre (1667-1754), son of a surgeon, was born in Vitry-le-Francois, France. His
- 4. Generating functions He did not receive good training in mathematics until he moved to Paris in
- 5. Generating functions Around 1686, De Moivre emigrated to England, where he began his lifelong profession, tutoring
- 6. Generating functions Unfortunately, despite his influential friends, he could not find an academic position. He had
- 7. Generating functions He dedicated his first book, a masterpiece, The Doctrine of Chances, to Newton. His
- 8. Generating functions
- 9. Generating functions
- 10. Generating functions
- 11. Generating functions
- 12. Generating functions
- 13. Generating functions
- 14. Generating functions
- 15. Generating functions
- 16. Generating functions
- 17. Generating functions Can we add and multiply generating functions? Yes! Such operations are performed exactly the
- 18. Generating functions
- 19. Generating functions
- 21. Generating functions
- 22. Generating functions
- 23. Generating functions
- 24. Generating functions
- 31. Example 3
- 32. Example 3
- 33. Example 3
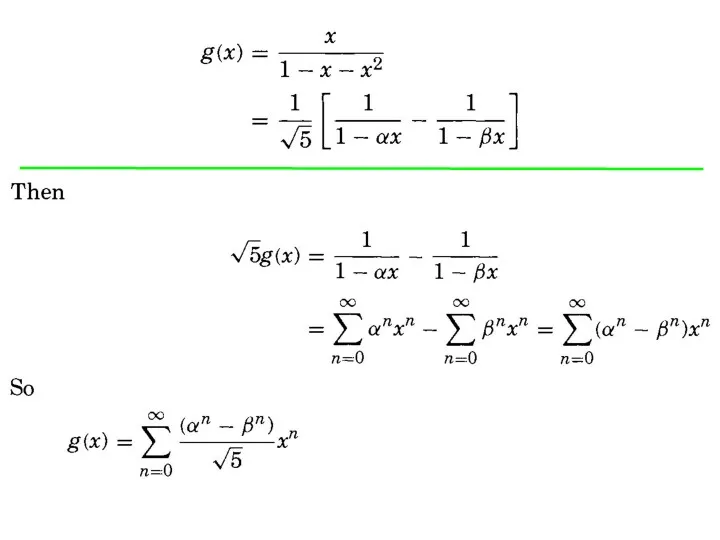
- 34. Generating functions Now we are ready to use partial fraction decompositions and generating functions to solve
- 35. Example 4
- 36. Example 4
- 38. 1 slide 11
- 39. Example 5
- 40. Example 5 2
- 42. Example 5
- 43. Example 6
- 44. Example 6
- 45. Example 6
- 47. Скачать презентацию


















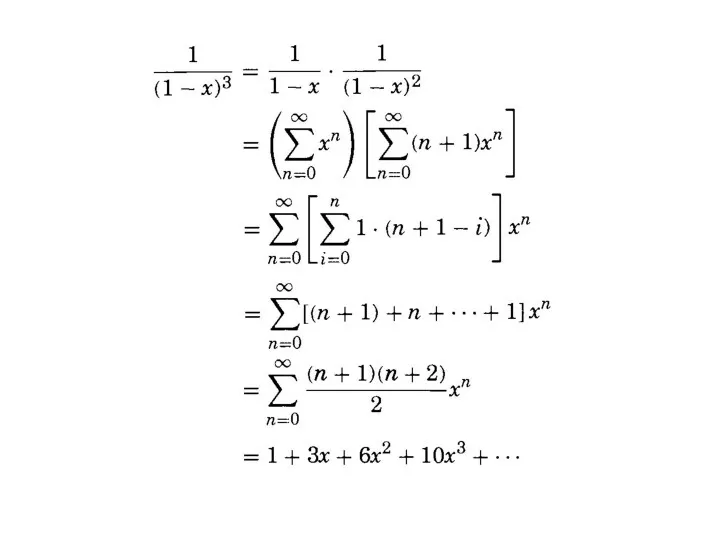
























 Основы комбинаторики. Лекция 1
Основы комбинаторики. Лекция 1 Конус. Властивості конуса
Конус. Властивості конуса Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Линейные дискретные системы. Структура звеньев второго порядка
Линейные дискретные системы. Структура звеньев второго порядка Интеллектуальная игра Танграм. Тема Система
Интеллектуальная игра Танграм. Тема Система Смежные и вертикальные углы
Смежные и вертикальные углы Комбинаторика. Размещения и сочетания. Дискретный анализ. Лекция 4
Комбинаторика. Размещения и сочетания. Дискретный анализ. Лекция 4 Арифметический квадратный корень
Арифметический квадратный корень Открытый урок математики во 2 классе и отчет за аттестационный период
Открытый урок математики во 2 классе и отчет за аттестационный период Тренажер по математике Сложение и вычитание
Тренажер по математике Сложение и вычитание Площадь трапеции
Площадь трапеции Рациональные неравенства. Тест
Рациональные неравенства. Тест Решение задач методом координат. 5 класс
Решение задач методом координат. 5 класс Компоненты вычитания
Компоненты вычитания Для подготовки к контрольной работе за 3 четверть
Для подготовки к контрольной работе за 3 четверть Calculation of the determinants + verifiation
Calculation of the determinants + verifiation Экологическая викторина. Жизнь в стиле ЭКО
Экологическая викторина. Жизнь в стиле ЭКО Теоремы Чевы и Менелая. 9 класс
Теоремы Чевы и Менелая. 9 класс Математика в стихах. 5 класс
Математика в стихах. 5 класс Описанная и вписанная окружности треугольника
Описанная и вписанная окружности треугольника Формулы приведения. Тригонометрия-10 класс
Формулы приведения. Тригонометрия-10 класс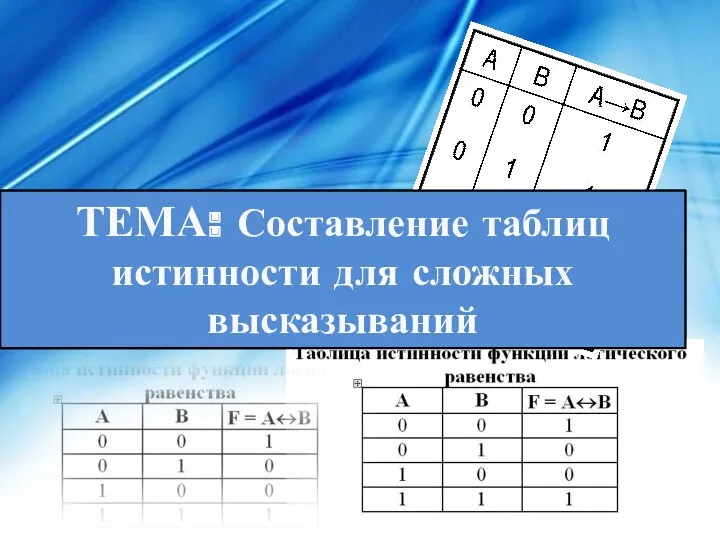 Составление таблиц истинности для сложных высказываний
Составление таблиц истинности для сложных высказываний Способы решения систем линейных уравнений (7 класс)
Способы решения систем линейных уравнений (7 класс) Трехгранные и многогранные углы
Трехгранные и многогранные углы Графический способ решения уравнений и систем уравнений в среде Microsoft Excel
Графический способ решения уравнений и систем уравнений в среде Microsoft Excel Математическая сказка о Колобке. Для 5 класса
Математическая сказка о Колобке. Для 5 класса Математика в ДОУ
Математика в ДОУ Парная регрессия и корреляция
Парная регрессия и корреляция