Содержание
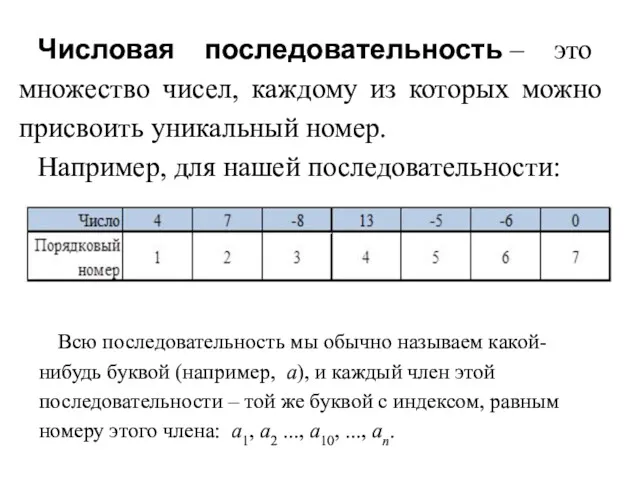
- 2. Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер. Например, для нашей
- 3. Определение 1. Функцию вида у= f (х), х ϵ Ν называют функцией натурального аргумента или числовой
- 4. Свойства числовых последовательностей Последовательность {an} называется монотонной, если an+1≥ an или an+1≤an для всех n. В
- 5. Если существует такое натуральное T, что, начиная с некоторого n, выполняется равенство an = an+1, то
- 6. Примеры бесконечных числовых последовательностей 1, 2, 3, 4, 5, … - последовательность натуральных чисел. 2, 4,
- 7. Способы задания числовых последовательностей Словесный Аналитический Рекуррентный
- 8. Словесный способ. Правило задания описано словами, без указания каких-либо формул или когда закономерности между элементами последовательности
- 10. Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6… Продолжите ряд 77, 49,
- 11. Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6… Продолжите ряд 77, 49,
- 12. Аналитический способ задания числовых последовательностей Последовательность задана аналитически, если указана формула n-ого члена. Например, yn=n2 –
- 13. Рекуррентный способ задания числовых последовательностей Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее
- 14. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610… Числа
- 15. Последовательность чисел Фибоначчи Филлотаксис (листорасположение) — правило, по которому располагаются, например, семечки в соцветии подсолнуха. Семечки
- 16. Арифметическая прогрессия Пример: 1, 3, 5, 7, 9, 11, … возрастающая арифметическая прогрессия, у которой d
- 18. Геометрическая прогрессия Пример: 54 , 18, 6, 2, … -убывающая геометрическая прогрессия, у которой q =
- 19. Развитие учения о прогрессиях Прогрессия (от латинского progressio) -«движение вперёд» Наблюдая луну от новолуния до полнолуния,
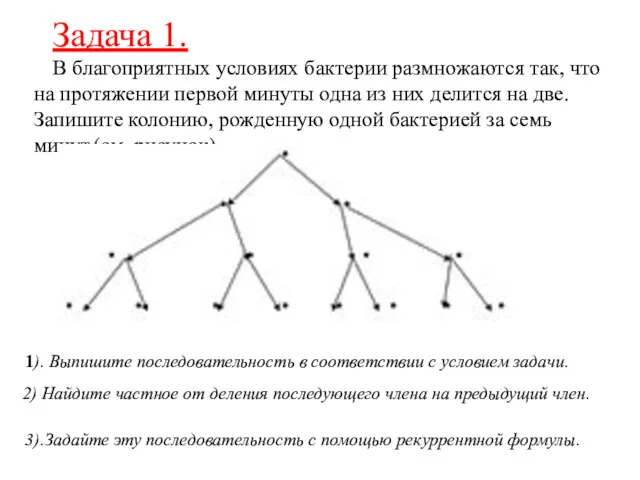
- 20. Задача 1. В благоприятных условиях бактерии размножаются так, что на протяжении первой минуты одна из них
- 21. Решение: 1). Выпишите последовательность в соответствии с условием задачи. 1;2;4;8;16;32;64. или (bп) - последовательность, b1 =1;
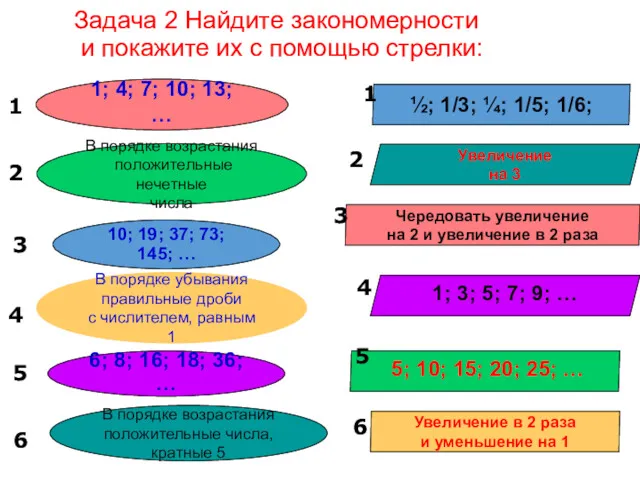
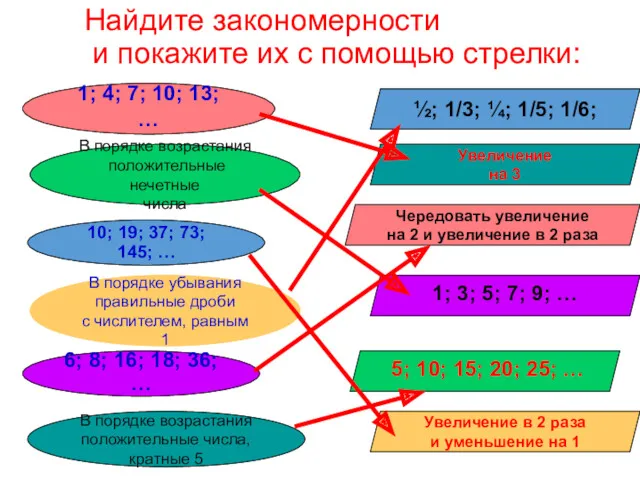
- 22. Задача 2 Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; …
- 23. Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке
- 24. Задача 3 Определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической: 3; 6; 12; 24;
- 25. Сравним наши ответы: Геометрическая прогрессия – 3, 6. Арифметическая прогрессия – 2, 4. Не является ни
- 26. Геометрическая прогрессия {bn} - это числовая последовательность, первый член которой отличен от нуля, а каждый член,
- 27. Вернемся к нашей последней прогрессии q=−3, а b1=4 и попробуем так же как и в арифметической
- 28. Бесконечно убывающая геометрическая прогрессия. Совсем недавно мы говорили о том, что q может быть как больше,
- 29. Свойство арифметической прогрессии. an=(an+1+an−1)/2 - свойство членов арифметической прогрессии. Свойство геометрической прогрессии. Как найти b3, зная
- 31. Сумма членов геометрической прогрессии.
- 32. Формулы для прогрессий
- 33. Задача 5 Ученик 5 А класса Вася, заболел гриппом, но продолжает ходить в школу. Каждый день
- 35. Скачать презентацию




























 Занимательная математика
Занимательная математика Многозначные числа урок по математике 3 класс
Многозначные числа урок по математике 3 класс Решение задач составлением систем линейных уравнений с двумя переменными
Решение задач составлением систем линейных уравнений с двумя переменными Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики
Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация к уроку Выделение в числе общего количества единиц любого разряда 4 класс
Презентация к уроку Выделение в числе общего количества единиц любого разряда 4 класс II признак равенства треугольников
II признак равенства треугольников Треугольник. Признаки равенства треугольников
Треугольник. Признаки равенства треугольников Письменный прием сложения вида 37+48
Письменный прием сложения вида 37+48 Статистические ряды распределения
Статистические ряды распределения Презентация к уроку математики в 1 классе.
Презентация к уроку математики в 1 классе. Математика 4 класс. Время. Скорость Расстояние.
Математика 4 класс. Время. Скорость Расстояние. Конспект урока математики на тему: Сложение и вычитание в пределах 20.
Конспект урока математики на тему: Сложение и вычитание в пределах 20. Презентация Вычитание. Название компонентов и результат действия
Презентация Вычитание. Название компонентов и результат действия Деление на двузначное число 3 класс
Деление на двузначное число 3 класс Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Открытый банк заданий по математике. ЕГЭ. Задания В 12
Открытый банк заданий по математике. ЕГЭ. Задания В 12 Презентация Взаимное расположение 2-х окружностей
Презентация Взаимное расположение 2-х окружностей Развитие теории вероятностей. Основные элементы комбинаторики
Развитие теории вероятностей. Основные элементы комбинаторики Решение задач. Сумма углов треугольника. Внешний угол треугольника
Решение задач. Сумма углов треугольника. Внешний угол треугольника Математика - царица всех наук. Математический турнир
Математика - царица всех наук. Математический турнир Свойства числовых неравенств математика
Свойства числовых неравенств математика Метод наименьших квадратов
Метод наименьших квадратов Устный счёт 4 класс
Устный счёт 4 класс Стохастическая модель образования очереди у однополосного регулируемого перекрёстка
Стохастическая модель образования очереди у однополосного регулируемого перекрёстка Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел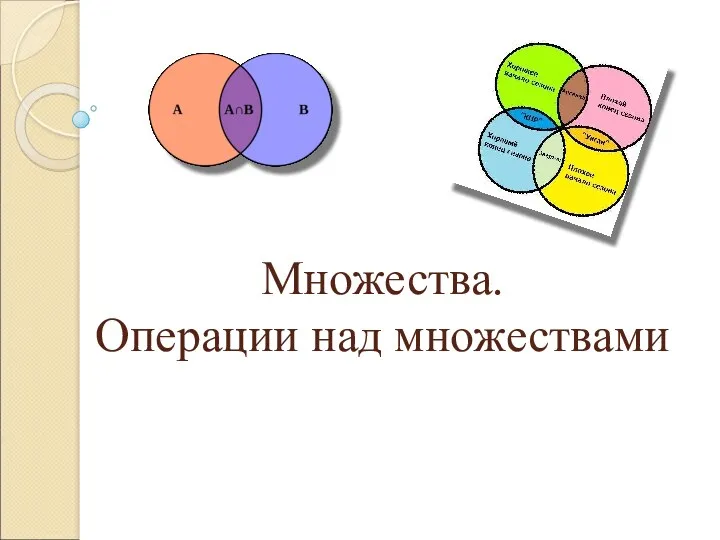 Множества. Операции над множествами
Множества. Операции над множествами Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник