Содержание
- 2. План лекции: 1. Критерии проверки статистических гипотез 2. Параметрические критерии: Критерий Стьюдента, Критерий Фишера 3. Непараметрические
- 3. Основные понятия: Нулевая гипотеза Альтернативная гипотеза Ошибки первого и второго рода Уровень значимости
- 4. Этапы проверки статистических гипотез Формулировка основной гипотезы H0 и конкурирующей гипотезы H1. Гипотезы должны быть чётко
- 5. Статистическая гипотеза - некоторое предположение о свойствах генеральной совокупности, которой принадлежит выборка.
- 6. Нулевая гипотеза (Н0) - предположение о том, что между генеральными параметрами сравниваемых групп разница равна нулю,
- 7. Если выборка из совокупности 1 имеет параметры µ1 и σ1, а выборка из совокупности 2 соответственно
- 8. Нулевая гипотеза может иметь в виду µ=α, где α- какое-то число.
- 9. Альтернативная (противоположная) гипотеза – противопоставляется нулевой гипотезе и исходит из того, что: µ1-µ2≠0 и σ1-σ2≠0
- 10. Критерии проверки гипотез: Число степеней свободы (k) – числа, показывающие количество свободно варьирующих элементов или членов
- 11. Критерии значимости Параметрические Критерий Стьюдента (t) Критерий Фишера (F) Непараметрические Критерий Хи-квадрат (χ²) Критерий Колмогорова-Смирнова (d)
- 12. Параметрические критерии строятся на основе параметров выборочной совокупности Непараметрические критерии функции от вариант данной совокупности с
- 13. Область значений случайной величины Область допустимых значений Область маловероятных значений
- 14. Критическое значение – соответствует границе между областью допустимых и областью маловероятных значений. Устанавливается в зависимости от
- 15. Выделяют три вида критических областей: Двусторонняя критическая область определяется двумя интервалами, где находят из условий .
- 16. Ошибка первого рода Уровень значимости характеризует ту вероятность, которой решено пренебрегать в данном исследовании. Отклонение нулевой
- 17. Ошибка второго рода Принятие нулевой гипотезы, когда она неверна, носит название ошибки второго рода. Вероятность такой
- 18. Уменьшая вероятность ошибки первого рода (α), мы неизбежно увеличиваем вероятность ошибки второго рода (β). Выбор уровня
- 19. Параметрические критерии
- 20. Распределение Стьюдента (или t-распределение) - это распределение отклонений нормально распределенной случайной величины от генерального среднего, нормированных
- 21. Классическим примером распределения Стьюдента является распределение стандартизованных отклонений где: х - нормально распределенное выборочное среднее; µ-
- 22. Кривая распределения Стьюдента похожа по внешнему виду на кривую нормального распределения: она одновершинна, симметрична, ее ветви
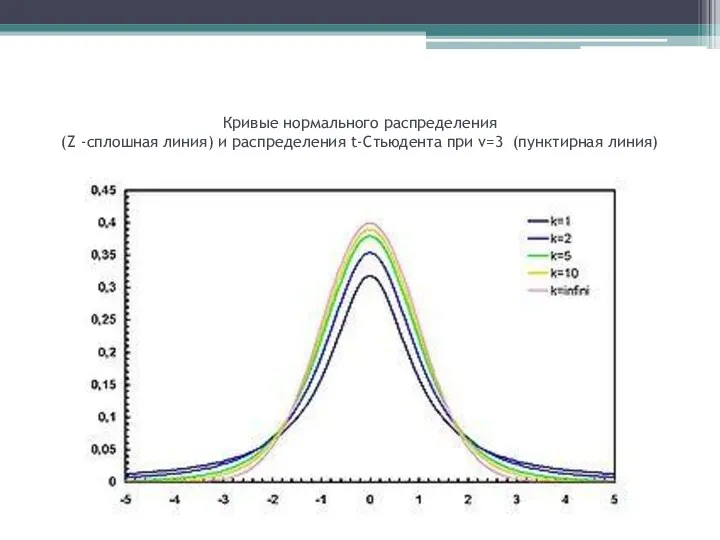
- 23. Кривые нормального распределения (Z -сплошная линия) и распределения t-Cтьюдента при ν=3 (пунктирная линия)
- 24. Наибольшее отличие распределения Стьюдента от нормального наблюдается при ν=1, когда при значениях переменной величины t, близких
- 26. t – распределение – частный случай нормального распределения; t – распределение – симметрично; t – распределение
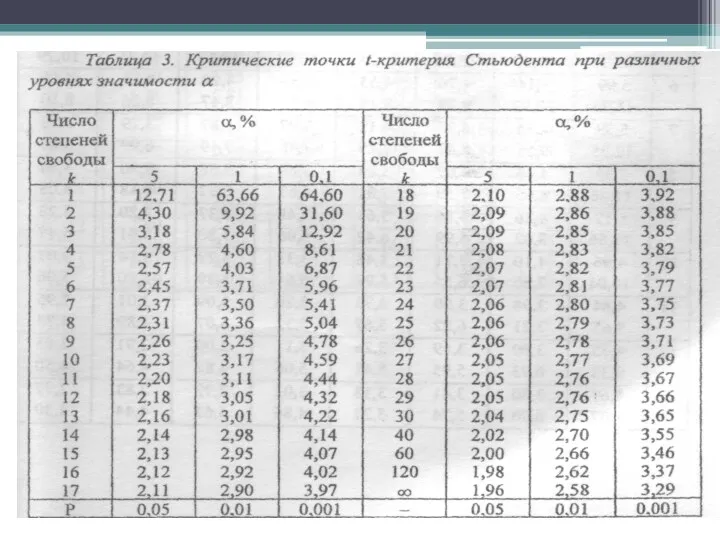
- 28. Сравнение средних арифметических корреляционно не связанных между собой выборок, взятых из нормально распределяющихся совокупностей с их
- 29. Нулевая гипотеза опровергается (Н0), если tф≥tst для принятого уровня значимости и числа степеней свободы k=n1+n2-2.
- 30. Распределение F Фишера. Распределение представляющее собой случайную величину, распределение которой было изучено Фишером, названо его именем
- 31. Если имеются две оценки S1² и S2² одной и той же дисперсии σ² нормально распределенной случайной
- 32. С увеличением v1 и ν2 обе оценки стремятся к одному и тому же параметру σ², F
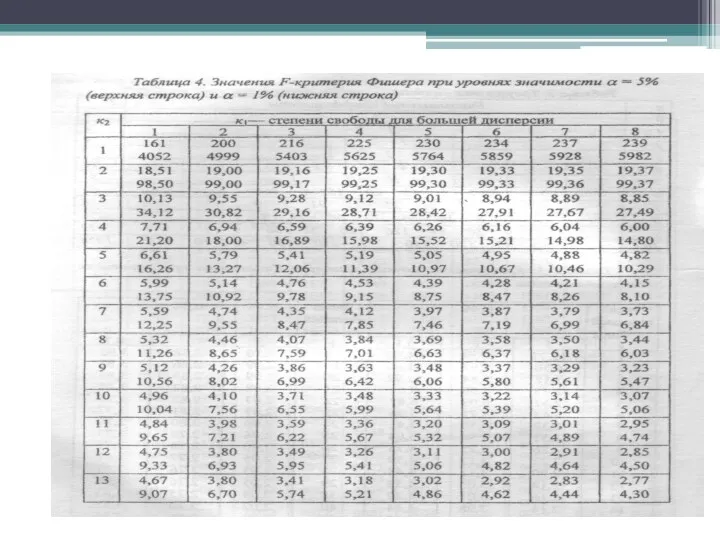
- 33. Распределение F зависит от числа степеней свободы ν1 и ν2, с которыми найдены оценки дисперсий в
- 35. Если выборки взяты из разных совокупностей с неравными параметрами σ1² и σ2², то Fф≥Fst и нулевая
- 36. Непараметрические критерии
- 37. Распределение Хи-квадрат (χ2(n)) Допустим, что случайная величина Z распределена нормально с параметрами . Если взять n
- 38. Основные свойства критерия: Случайная величина χ2, будучи суммой квадратов, всегда положительна и должна зависеть от числа
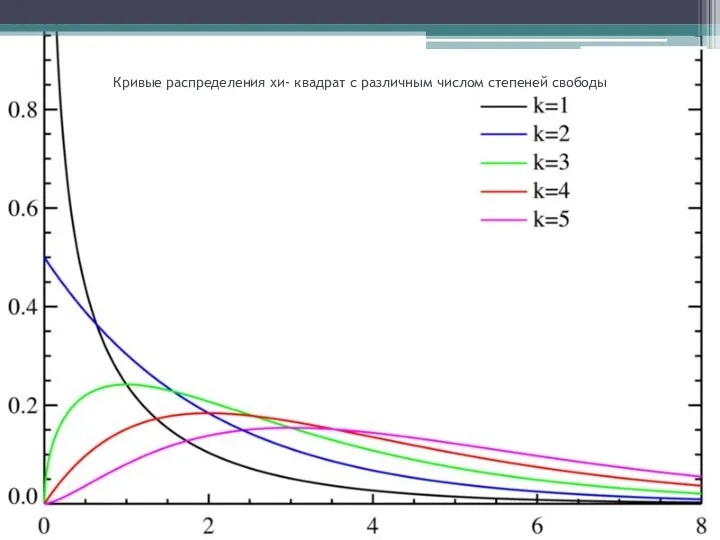
- 39. Вид кривой распределения существенно зависит от числа слагаемых, точнее, от числа независимых слагаемых, т.е. от числа
- 40. Кривые распределения хи- квадрат с различным числом степеней свободы
- 41. Так как закон распределения известен, то не составляет большого труда вычислить критические значения χα2, случайно превысить
- 42. Для выборок равного объема, n1=n2 и N= n1+n2
- 43. Для выборок разного объема, n1≠n2
- 44. При сравнении эмпирического и теоретического распределения формула используют формулу
- 46. U-критерий Манна-Уитни (англ. Mann-Whitney U test) — непараметрический статистический критерий, используемый для оценки различий между двумя
- 47. Простой непараметрический критерий. Метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом
- 48. Для применения U-критерия Манна-Уитни нужно произвести следующие операции: 1. Составить единый ранжированный ряд из обеих сопоставляемых
- 49. 2. Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок. Подсчитать
- 50. 3. Определить значение U-критерия Манна-Уитни по формуле:
- 51. 4. По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных n1 и
- 52. 5. При справедливости нулевой гипотезы критерий имеет матожидание и дисперсию и при достаточно большом объёме выборочных
- 54. Ограничения применимости критерия 1. В каждой из выборок должно быть не менее 3 значений признака. Допускается,
- 55. Критерий Колмогорова -Смирнова В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова-Смирнова) используется для
- 56. Критерий Колмогорова-Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных и
- 57. Максимальная по модулю разность между соответствующими накопленными относительными частотами является фактическим значением критерия Колмогорова-Смирнова.
- 58. Теоретическое значение критерия Колмогорова Смирнова вычисляется по формуле:
- 61. Скачать презентацию





































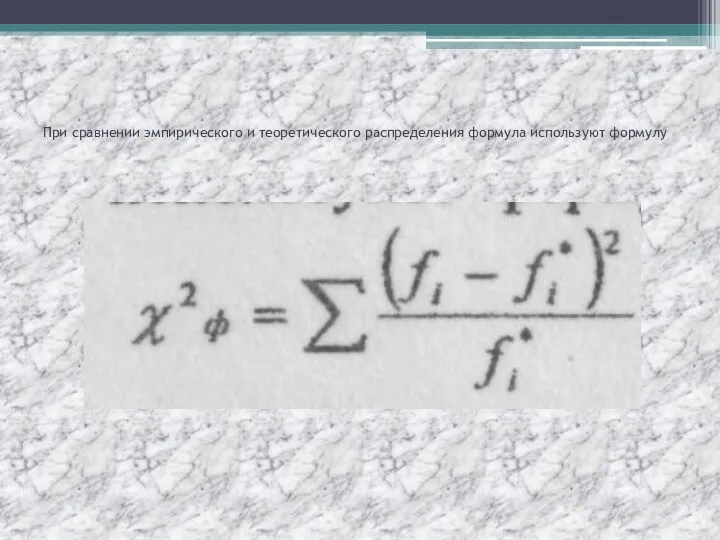















 Задачи 1-32 по математике
Задачи 1-32 по математике Сравнение многозначных чисел.
Сравнение многозначных чисел. Лекція 3. Тема 1.3. Метричні і позиційні властивості прямокутних проекцій пар елементарних геометричних фігур
Лекція 3. Тема 1.3. Метричні і позиційні властивості прямокутних проекцій пар елементарних геометричних фігур Разложение многочленов на множители с помощью ФСУ
Разложение многочленов на множители с помощью ФСУ Сложение чисел с разными знаками
Сложение чисел с разными знаками Сумма углов треугольника
Сумма углов треугольника Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс
Задачи на нахождение дроби от числа и числа по его части. Математика. 5 класс Урок - КВН. Четырехугольники и их площади
Урок - КВН. Четырехугольники и их площади Совершенствование навыков решения задач по теме Треугольники
Совершенствование навыков решения задач по теме Треугольники Mathematics for еconomists. (Week 1-12)
Mathematics for еconomists. (Week 1-12) Математические модели и их классификации (Лекция № 2)
Математические модели и их классификации (Лекция № 2) Презентация Нахождение площади прямоугольника
Презентация Нахождение площади прямоугольника Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Методы оптимизации объектов
Методы оптимизации объектов День защитника отечества. Урок математики
День защитника отечества. Урок математики Все действия с положительными и отрицательными числами. 6 класс
Все действия с положительными и отрицательными числами. 6 класс Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Открытый урок по математике в 3-м классе Единица времени - сутки
Открытый урок по математике в 3-м классе Единица времени - сутки Деление и дроби. Представление натуральных чисел дробями
Деление и дроби. Представление натуральных чисел дробями Розв'язуємо задачі на різницеве порівняння двох добутків. Урок №81
Розв'язуємо задачі на різницеве порівняння двох добутків. Урок №81 ТЕСТ-ИГРА Умножение и деление круглых чисел
ТЕСТ-ИГРА Умножение и деление круглых чисел Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Особенности поведения сложных систем. Лекция
Особенности поведения сложных систем. Лекция Утворення, запис, читання чисел
Утворення, запис, читання чисел Комбинаторика. Урок 1
Комбинаторика. Урок 1 группировка слагаемых
группировка слагаемых Прямоугольный параллелепипед
Прямоугольный параллелепипед Общее уравнение кривой второго порядка. Аналитическая геометрия
Общее уравнение кривой второго порядка. Аналитическая геометрия