Содержание
- 2. 1 Если произвести большое число выборок равного объема из генеральной совокупности, то для каждой выборки мы
- 3. 2 При некоторых достаточно общих предположениях о распределении в генеральной совокупности (конечность средних и ограниченность дисперсии),
- 4. 3 Пусть из генеральной совокупности отобрана случайная выборка x1, x2, x3 …xn . Следует найти наилучшую
- 5. 4 В качестве оценки среднего значения можно взять и полусумму максимального и минимального значений. Какая оценка
- 6. 5 Оценка параметра Х называется несмещенной, если математическое ожидание оценки равно ее истинному значению при любом
- 7. 6 Несмещенная оценка называется эффективной, если она обладает наименьшей дисперсией. Используемые оценки не всегда являются эффективными,
- 8. 2.9. Свойства выборочной средней и дисперсии
- 9. 2 Выборочная средняя является несмещенной оценкой генеральной средней. Доказательство . Пусть выборочная средняя определяется формулой Будем
- 10. 3 Действительно, из определения математического ожидания имеет то же распределения, что и случайная величина Х в
- 11. 4 Будем рассматривать выборочные средние как случайные величины. Найдем дисперсию среднего арифметического одинаково распреде-ленных случайных величин
- 12. 5 Среднее квадратическое отклонение выборочных средних, которое обозначено буквой можно использовать для оценки по порядку величины
- 13. 2.10. Оценка генеральной дисперсии по выборочной
- 14. 1 Очень часто дисперсия в генеральной совокупности является неизвестной величиной и ее нужно оценить по выборочной
- 15. 2 Поэтому на практике в качестве оценки генеральной дисперсии используют исправленную выборочную дисперсию , математическое ожидание
- 16. 2.11. Доверительный интервал и доверительная вероятность
- 17. 1 До сих пор оценку параметров генеральной совокупности мы производили одним числом. Такая оценка называется точечной.
- 18. 2 Определение Интервальной оценкой параметра Х называется числовой интервал ( ) , который с заданной вероятностью
- 19. 3 Нас интересует ошибка конкретной выборки. Поэтому введем понятие нормированного отклонения, обозначив его буквой t: Эта
- 20. 4 Ошибки репрезентативности выборочного обследования избежать нельзя, но можно потребовать, чтобы вероятность отклонения выборочной средней от
- 21. 5 Для определения величины интервала, который с заданной с заданной доверительной вероятностью накроет среднее значение мы
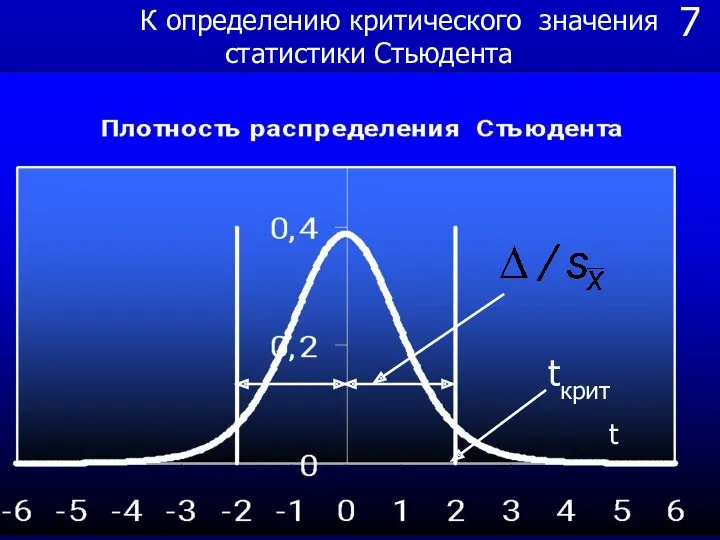
- 22. 6 Зная величину по таблице распределения Стьюдента или с помощью функции Excel СТЬЮДРАСПОБР(q;k), q =(1-P); где
- 23. 7 К определению критического значения статистики Стьюдента t tкрит
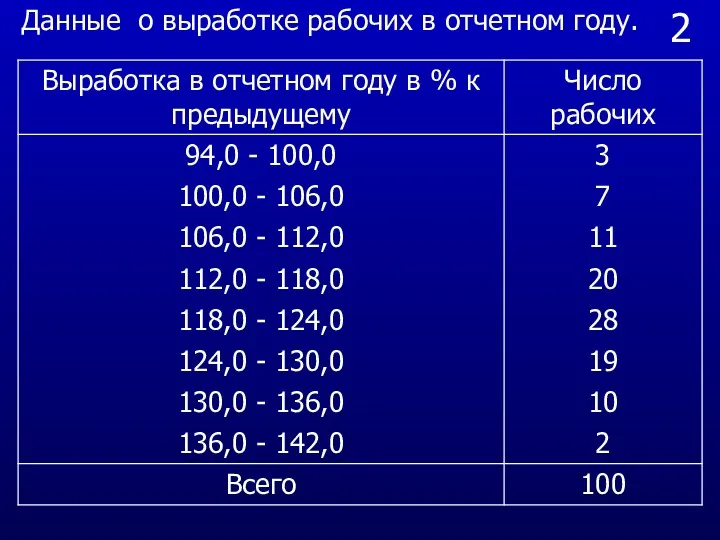
- 24. Задача При обследовании выработки 1000 рабочих цеха в отчетном году по сравнению с предыдущим по схеме
- 25. 2 Данные о выработке рабочих в отчетном году.
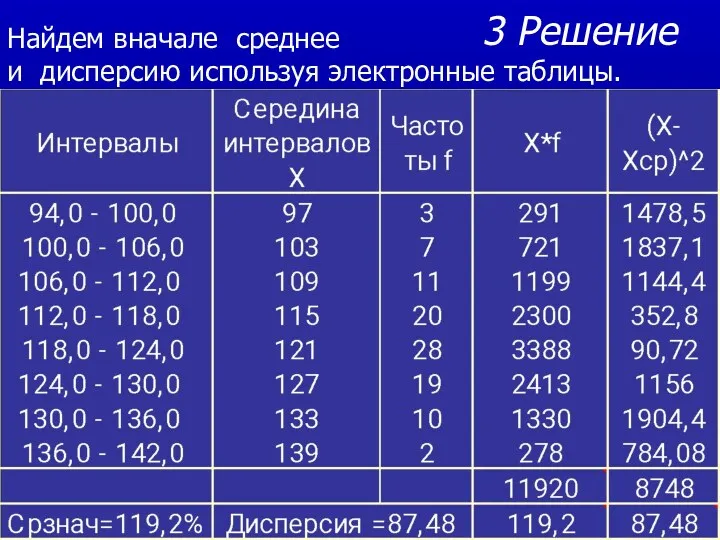
- 26. 3 Решение Найдем вначале среднее и дисперсию используя электронные таблицы.
- 27. 4 Найдем среднеквадратическую ошибку выборки для средней:
- 28. 5 Искомую доверительную вероятность найдем из условия ( = 1 %), k=7 Таким образом, вероятность того,
- 30. Скачать презентацию
























 Математика и живопись
Математика и живопись Геометрические фигуры. Точка
Геометрические фигуры. Точка Арифметическая и геометрическая прогрессия. Обобщение и систематизация теоретического материала
Арифметическая и геометрическая прогрессия. Обобщение и систематизация теоретического материала Геометрическое место точек (7 класс)
Геометрическое место точек (7 класс) Устный счёт для второклассников.
Устный счёт для второклассников. Углы. Виды углов. 7 класс
Углы. Виды углов. 7 класс Внеурочная деятельность. Логика. 1 класс. Последовательность действий и событий.
Внеурочная деятельность. Логика. 1 класс. Последовательность действий и событий.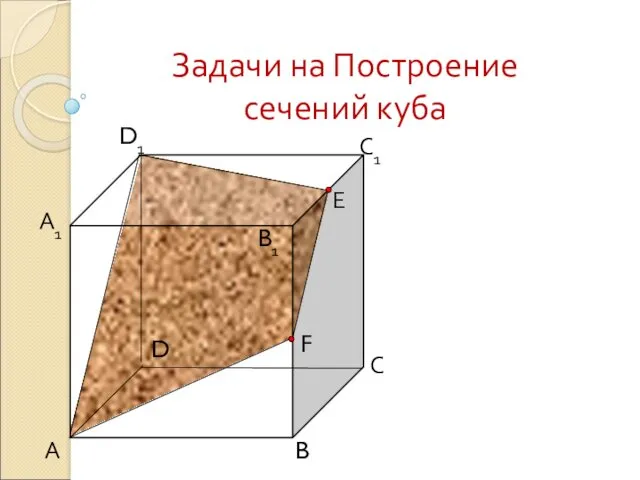 Задачи на Построение сечений куба
Задачи на Построение сечений куба Развитие логического мышления средствами спецкурса по математике Математический калейдоскоп
Развитие логического мышления средствами спецкурса по математике Математический калейдоскоп Состав числа в приделах 10. Закрепление изученного
Состав числа в приделах 10. Закрепление изученного Нормальное распределение
Нормальное распределение Дни недели.
Дни недели. Иррациональные уравнения и неравенства
Иррациональные уравнения и неравенства Уведення поняття кілограм
Уведення поняття кілограм Фигуры и тренировочные листы с задачами и примерами
Фигуры и тренировочные листы с задачами и примерами Векторы в пространстве и действия над ними. Компланарные векторы
Векторы в пространстве и действия над ними. Компланарные векторы Тела вращения
Тела вращения Цилиндр. 9 класс
Цилиндр. 9 класс Задача на знаходження решти. Відтворення малюнка
Задача на знаходження решти. Відтворення малюнка Длина окружности и площадь круга
Длина окружности и площадь круга Перпендикулярные прямые
Перпендикулярные прямые Числовые и буквенные выражения. Уравнения
Числовые и буквенные выражения. Уравнения Алгебра матриц. Комплексные числа
Алгебра матриц. Комплексные числа Открытый урок математики во 2 классе и отчет за аттестационный период
Открытый урок математики во 2 классе и отчет за аттестационный период Преобразование тригонометрических выражений (вывод тригонометрических формул)
Преобразование тригонометрических выражений (вывод тригонометрических формул) Окружность и круг
Окружность и круг График и свойства степенной функции
График и свойства степенной функции Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач
Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач