- Главная
- Математика
- Сюжетные задачи

Содержание
- 2. ПРЕМИИ В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам некоторого отдела на общую
- 3. а) Разделим общую сумму в 600 000 рублей на 40, получим, что каждый должен получить по
- 4. АВТОБУСЫ Группу школьников нужно перевези из летнего лагеря одним из двух способов: либо двумя автобусами типа
- 5. Тип А: 2 автобуса; n − рейсов каждый; m + 7 − человек в автобусе Тип
- 6. ДРОТИКИ В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до 20 и два центральных
- 7. а) Да, например, при попадании в утроение сектора 20, утроение сектора 19 и центральный сектор 50
- 8. б) Наибольшее количество очков, которое может набрать игрок одним броском ― 60 (утроение 20), далее идут:
- 9. в) Как было показано в пункте б) каждый бросок приносит игроку не более 60 очков. Значит,
- 10. ТЕСТ Участники одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается
- 12. б) В примере предыдущего пункта средний балл участников теста, сдавших тест, первоначально составлял 90 баллов, а
- 13. в) Пусть всего было N участников теста, сдали тест a участников, после добавления баллов сдали тест
- 14. МАЛЬЧИКИ/ДЕВОЧКИ
- 16. Скачать презентацию
ПРЕМИИ
В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам
ПРЕМИИ
В одном из заданий на конкурсе бухгалтеров требуется выдать премии сотрудникам
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, ели ведущему специалисту надо выдать 40 000 рублей, а остальные поделить поровну на 70 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
а) Разделим общую сумму в 600 000 рублей на 40, получим, что
а) Разделим общую сумму в 600 000 рублей на 40, получим, что
б) Сумма, оставшаяся после выплаты 40 000 будет равна 560 000. При делении на 70 сотрудников получаем выплаты по 8000 рублей. Не удастся сделать, так как 8000 = 5000 + 3 · 1000 и для 70 сотрудников нужно будет 210 тысячных купюр, а их всего 100.
в) Если премию можно распределять произвольным образом, то максимальное число будет соответствовать максимальному числу купюр, то есть 200 сотрудников.
АВТОБУСЫ
Группу школьников нужно перевези из летнего лагеря одним из двух способов:
АВТОБУСЫ
Группу школьников нужно перевези из летнего лагеря одним из двух способов:
Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа В входит на 7 человек меньше, чем в автобус типа А?
Тип А: 2 автобуса; n − рейсов каждый; m + 7 − человек в автобусе
Тип А: 2 автобуса; n − рейсов каждый; m + 7 − человек в автобусе
ДРОТИКИ
В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до
ДРОТИКИ
В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до
а) Может ли игрок тремя бросками набрать ровно 167 очков?
б) Может ли игрок шестью бросками набрать ровно 356 очков?
в) С помощью какого наименьшего количества бросков, игрок может набрать ровно 1001 очко?
а) Да, например, при попадании в утроение сектора 20, утроение сектора
а) Да, например, при попадании в утроение сектора 20, утроение сектора
б) Наибольшее количество очков, которое может набрать игрок одним броском ―
б) Наибольшее количество очков, которое может набрать игрок одним броском ―
в) Как было показано в пункте б) каждый бросок приносит игроку
в) Как было показано в пункте б) каждый бросок приносит игроку
Покажем, что игрок может набрать 1001 очко за 17 бросков. Предположим, что он сделал 15 бросков на 60 очков (итого 900), один бросок в зону утроения сектора 17 (51 очко) и один бросок в центральный сектор 50 очков. Тогда в сумме он наберет 900 + 51 + 50 = 1001 очко.
ТЕСТ
Участники одной школы писали тест. Результатом каждого ученика является целое неотрицательное
ТЕСТ
Участники одной школы писали тест. Результатом каждого ученика является целое неотрицательное
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 80, средний балл участников, сдавших тест, составил 90, а средний балл участников, не сдавших тест, составил 65. После добавления баллов средний балл участников, сдавших тест, стал равен 93, а не сдавших — 69. При каком наименьшем числе участников теста возможна такая ситуация?
б) В примере предыдущего пункта средний балл участников теста, сдавших тест,
б) В примере предыдущего пункта средний балл участников теста, сдавших тест,
в) Пусть всего было N участников теста, сдали тест a участников, после добавления баллов сдали
в) Пусть всего было N участников теста, сдали тест a участников, после добавления баллов сдали
Покажем, что N могло равняться 15. Пусть изначально 5 участников набрали по 64 балла, 1 участник — 70 баллов и 9 участников по 90 баллов. Тогда средний балл был равен 80, средний бал участников, сдавших тест, был равен 90, а средний балл участников, не сдавших тест, был равен 65. После добавления средний балл участников, сдавших тест, стал равен 93, средний балл участников, не сдавших тест, стал равен 69. Таким образом, все условия выполнены.
МАЛЬЧИКИ/ДЕВОЧКИ
МАЛЬЧИКИ/ДЕВОЧКИ













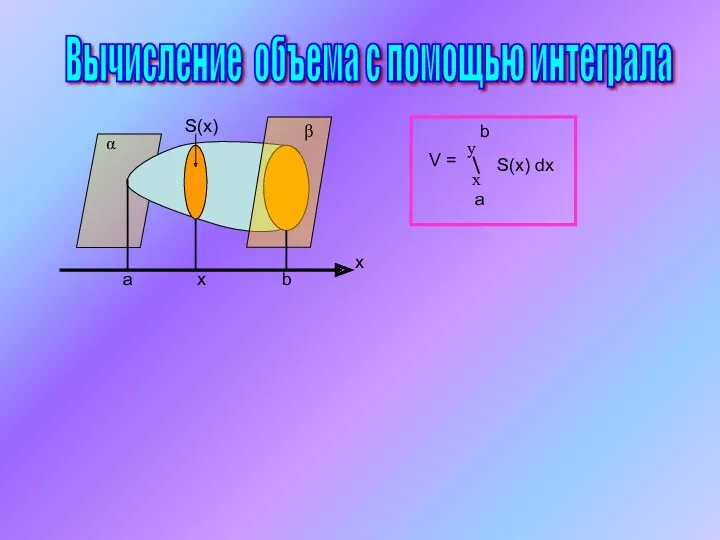 Вычисление объёма с помощью интеграла
Вычисление объёма с помощью интеграла Числовые промежутки. Геометрическая и аналитическая модели числового промежутка
Числовые промежутки. Геометрическая и аналитическая модели числового промежутка Замечательные пределы
Замечательные пределы Конкурс Любишь ли ты математику и знаешь ли ты её?
Конкурс Любишь ли ты математику и знаешь ли ты её? К 105-летию А.Линдгрен - Урок математики в 3 классе Деление двузначного числа на однозначное
К 105-летию А.Линдгрен - Урок математики в 3 классе Деление двузначного числа на однозначное Состав чисел в пределах 10. Закрепление
Состав чисел в пределах 10. Закрепление Эйлеровы графы. Пути и циклы Эйлера
Эйлеровы графы. Пути и циклы Эйлера Деление суммы на число
Деление суммы на число История развития геометрии
История развития геометрии Угол. Прямой и развёрнутый угол. Чертёжный треугольник
Угол. Прямой и развёрнутый угол. Чертёжный треугольник Метрологическое обеспечение сертификации. (Лекция 1)
Метрологическое обеспечение сертификации. (Лекция 1) Розв’язання лінійних рівнянь та систем лінійних рівнянь в пакеті Matlab
Розв’язання лінійних рівнянь та систем лінійних рівнянь в пакеті Matlab Пропорции. Задание для устного счета. Упражнение 17. 6 класс
Пропорции. Задание для устного счета. Упражнение 17. 6 класс Масштаб
Масштаб Олимпиада национальной технологической инициативы. Технологии беспроводной связи. Информатика. Математика
Олимпиада национальной технологической инициативы. Технологии беспроводной связи. Информатика. Математика презентация к уроку Умножение на трехзначное число со всеми значащими цифрами
презентация к уроку Умножение на трехзначное число со всеми значащими цифрами Мы - строители. Обучающая игра-тренажёр Часть 2
Мы - строители. Обучающая игра-тренажёр Часть 2 Приближённое вычисление определённого интеграла по формулам прямоугольников и трапеций. Оценка погрешности вычислений
Приближённое вычисление определённого интеграла по формулам прямоугольников и трапеций. Оценка погрешности вычислений Открытый урок математики
Открытый урок математики Презентация по математике Весёлое путешествие 1 класс
Презентация по математике Весёлое путешествие 1 класс Равносильность уравнений. Логарифмические уравнения
Равносильность уравнений. Логарифмические уравнения Математический калейдоскоп. Внеклассное мероприятие. 5 класс
Математический калейдоскоп. Внеклассное мероприятие. 5 класс Правильные и неправильные дроби. Понятия
Правильные и неправильные дроби. Понятия Главные направления линии второго порядка
Главные направления линии второго порядка Угол. Виды углов
Угол. Виды углов Описательная статистика. 7 класс
Описательная статистика. 7 класс Эмпирическая плотность распределения
Эмпирическая плотность распределения Подготовительный этап к изучению нумерации чисел первого десятка
Подготовительный этап к изучению нумерации чисел первого десятка