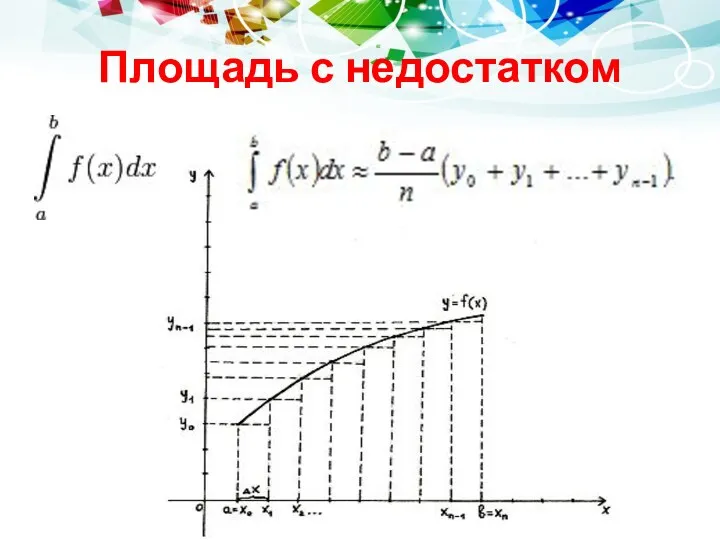
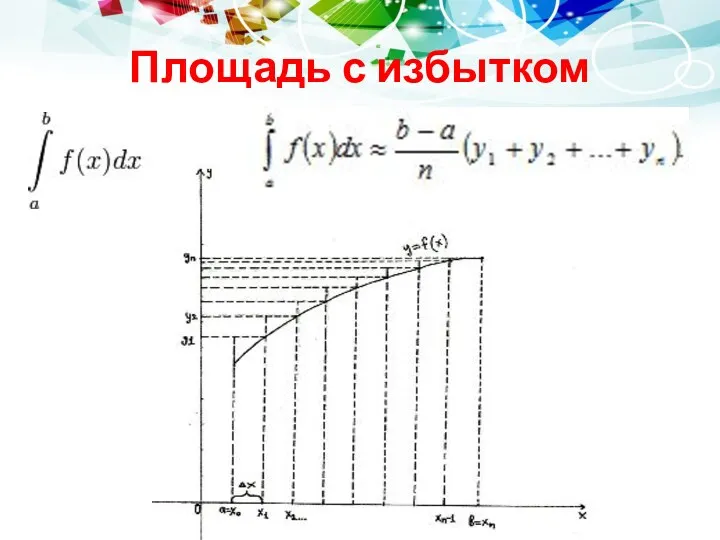
Алгоритм вычисления
Чтобы найти приближённое значение интеграла , нужно:
разделить отрезок интегрирования
[a, b] на n равных частей точками х0= а, х1, х2,..., х n -1, х n = b ;
вычислить значения подынтегральной функции в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ;
воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Значения у0, у1,..., уn находят из равенств , где
к = 0, 1..., n .Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.



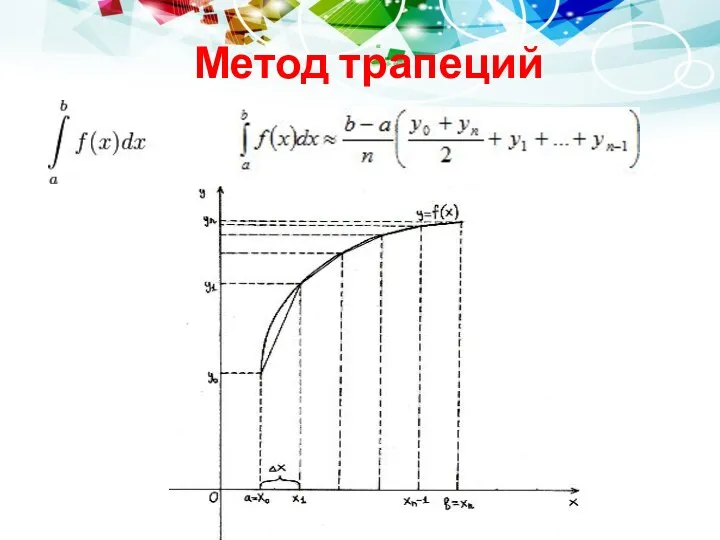
![Решение: Разобьём отрезок [a, b] на несколько (например, на 6)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598035/slide-6.jpg)

![Метод трапеций В этом методе отрезок [a;b] так же разбивается](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598035/slide-8.jpg)

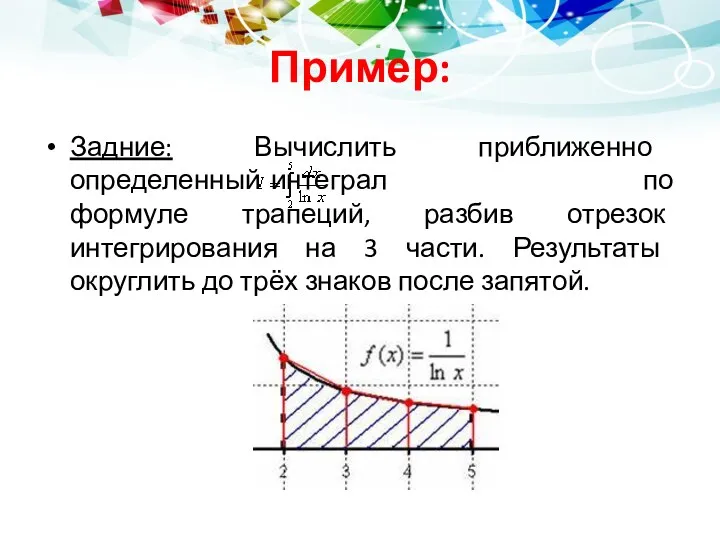
 Статистическая обработка данных
Статистическая обработка данных Діагностична робота з математики №3
Діагностична робота з математики №3 Пифагор Самосский
Пифагор Самосский Математический тренажер по теме Сложение и вычитание в пределах 20
Математический тренажер по теме Сложение и вычитание в пределах 20 Физико – математический турнир для учащихся 10-11 классов
Физико – математический турнир для учащихся 10-11 классов Модуль геометрия №11. ГИА 2013
Модуль геометрия №11. ГИА 2013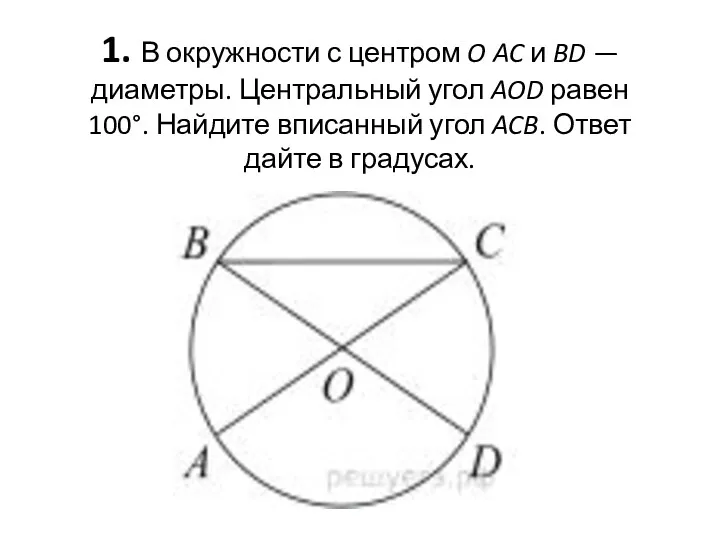 Окружности с центром O
Окружности с центром O Задачи со спичками
Задачи со спичками Устный счёт Новый год Диск
Устный счёт Новый год Диск Полуправильные многоугольники. Длина и площадь
Полуправильные многоугольники. Длина и площадь Критерии для проверки данных на соответствие нормальному закону распределения
Критерии для проверки данных на соответствие нормальному закону распределения У лукоморья. Физико-математический вечер
У лукоморья. Физико-математический вечер Треугольник
Треугольник Деление на двузначное число 3 класс
Деление на двузначное число 3 класс Элементы теории вероятностей. Элементы комбинаторики. (Лекция 3.4)
Элементы теории вероятностей. Элементы комбинаторики. (Лекция 3.4) Невизначений інтеграл
Невизначений інтеграл Прикладная математика и математическая логика. 1 семестр
Прикладная математика и математическая логика. 1 семестр Элементы комбинаторики и теории вероятностей
Элементы комбинаторики и теории вероятностей Приближение десятичных дробей. Урок 1
Приближение десятичных дробей. Урок 1 Четырехугольники. Наглядная геометрия. 6 класс
Четырехугольники. Наглядная геометрия. 6 класс Взаимно обратные функции
Взаимно обратные функции Начертательная геометрия. Взаимное пересечение поверхностей. (Лекция 8)
Начертательная геометрия. Взаимное пересечение поверхностей. (Лекция 8) Арифметикалық прогрессияның алғашқы nмүшесінің қосындысы
Арифметикалық прогрессияның алғашқы nмүшесінің қосындысы Весёлая таблица (тренажёр таблицы умножения и деления)
Весёлая таблица (тренажёр таблицы умножения и деления) Разработка внеклассного мероприятия по математике (викторина) для 5-9 классов
Разработка внеклассного мероприятия по математике (викторина) для 5-9 классов Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Умножение числа 6
Умножение числа 6 Неравенства с модулем. Способы решения неравенств с модулями
Неравенства с модулем. Способы решения неравенств с модулями