Содержание
- 2. «Скажи мне – и я забуду. Покажи мне – и я запомню. Вовлеки меня – и
- 3. Верно ли, что если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой
- 4. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? нет
- 5. Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости? нет
- 6. Хорда АВ принадлежит плоскости О, окружность не принадлежит данной плоскости
- 7. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны? нет
- 8. Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой? нет
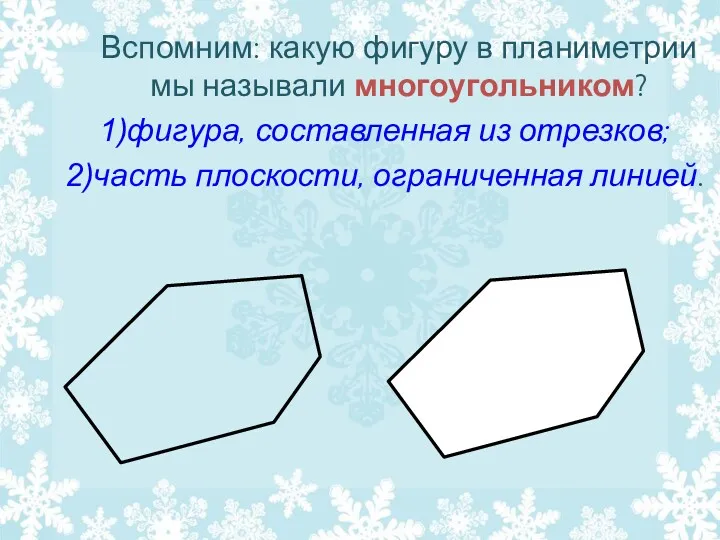
- 9. Вспомним: какую фигуру в планиметрии мы называли многоугольником? фигура, составленная из отрезков; часть плоскости, ограниченная линией.
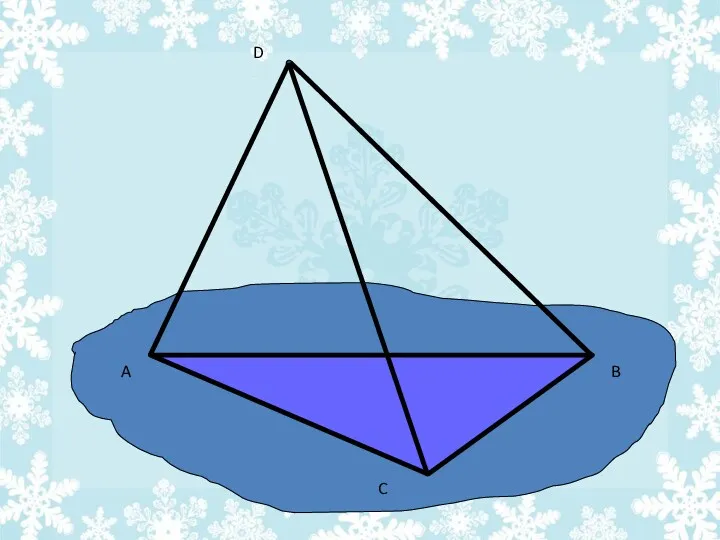
- 10. A B C D
- 11. Название этого многогранника пришло из Древней Греции, и в нем указывается число граней: «тетра» - 4
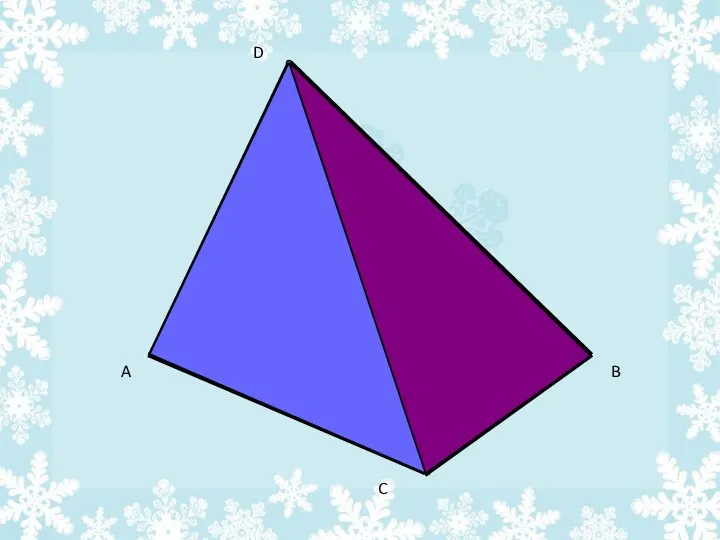
- 12. A B C D Поверхность, состоящая из четырех треугольников
- 13. Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной
- 14. Платоновы тела Гексаэдр Тетраэдр Октаэдр Икосаэдр Додекаэдр
- 15. Правильные многогранники в философской картине мира Платона Платон считал, что мир строится из четырёх «стихий» -
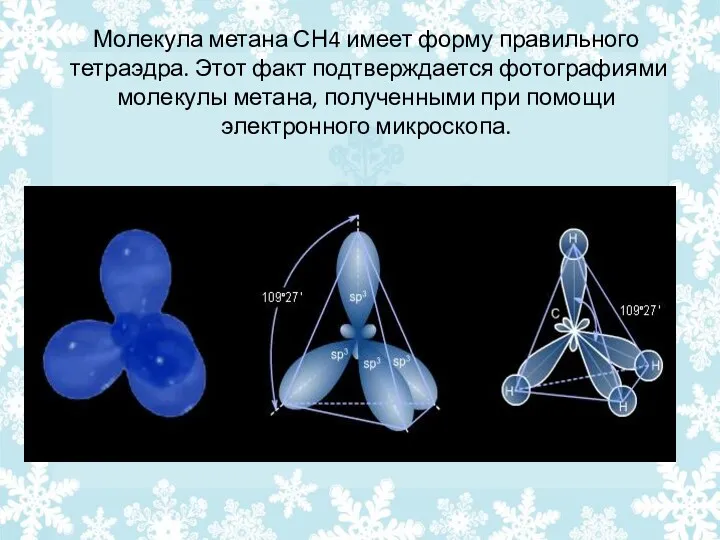
- 16. Молекула метана СН4 имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи
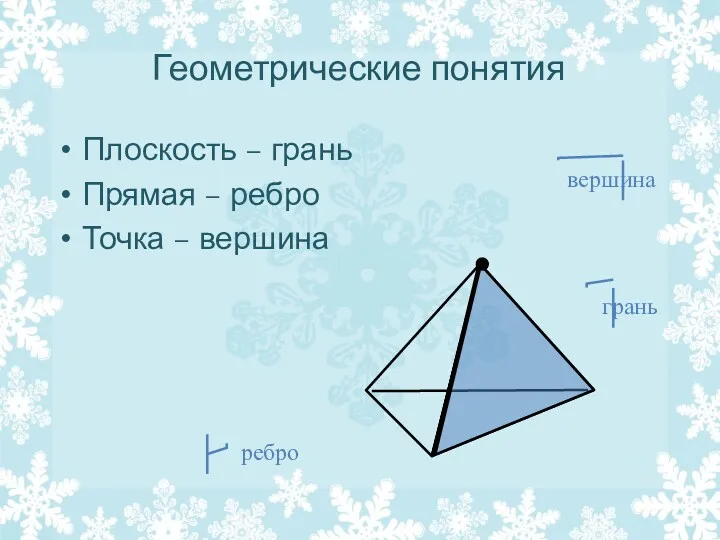
- 17. Геометрические понятия Плоскость – грань Прямая – ребро Точка – вершина грань ребро вершина
- 18. A B C D ТЕТРАЭДР ГРАНИ основание боковые грани
- 19. A B C D ТЕТРАЭДР ГРАНИ РЕБРА
- 20. A B C D ТЕТРАЭДР ГРАНИ РЕБРА противоположные
- 21. A B C D ТЕТРАЭДР ГРАНИ РЕБРА ВЕРШИНЫ
- 22. ТЕТРАЭДР. СЕЧЕНИЕ ТЕТРАЭДРА.
- 23. Определение тетраэдра: Поверхность, составленная из четырех треугольников, называется тетраэдром. Тетраэдр имеет: Граней-4; Ребер-6; Вершин-6.
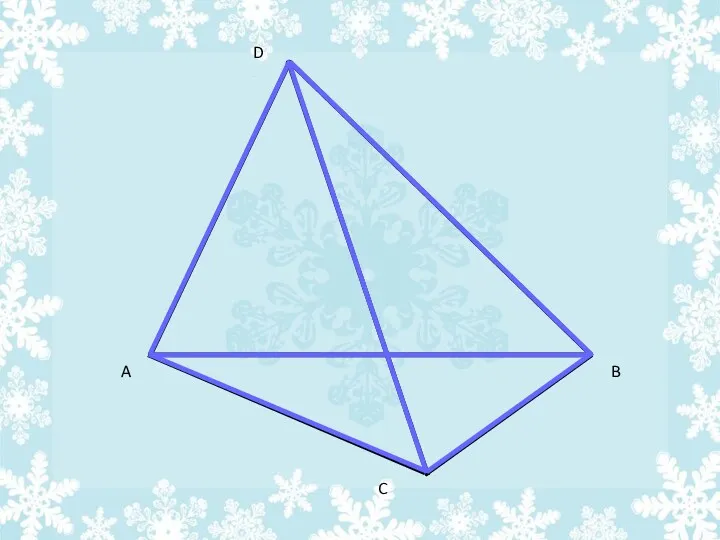
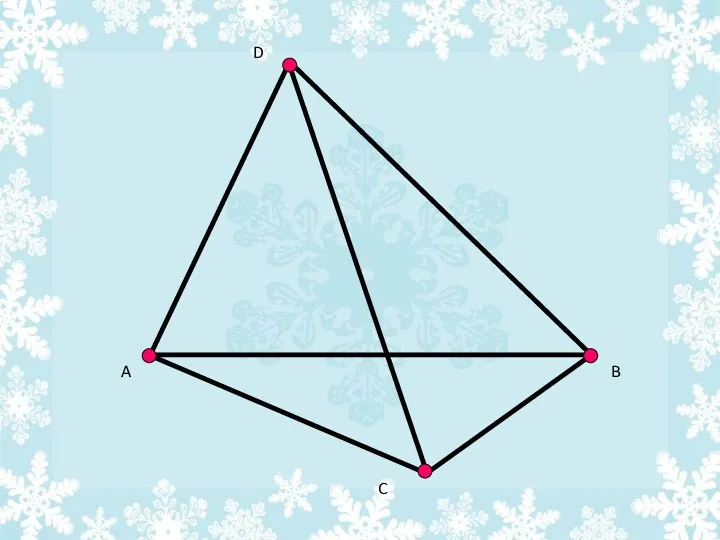
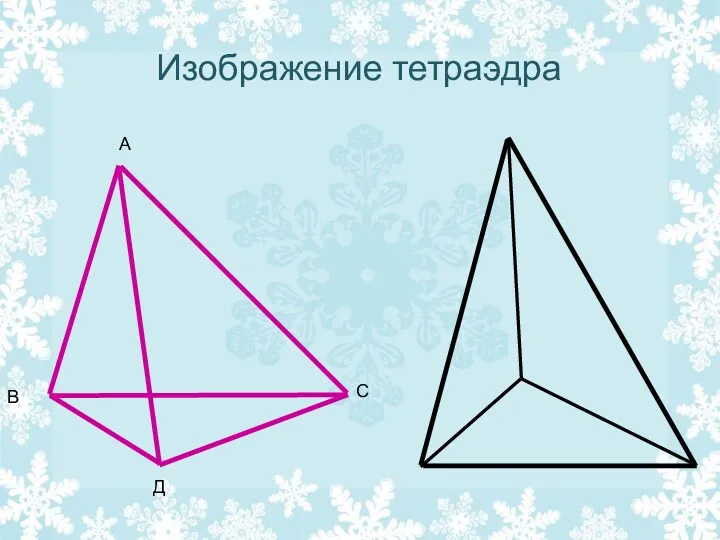
- 24. Изображение тетраэдра А В С Д
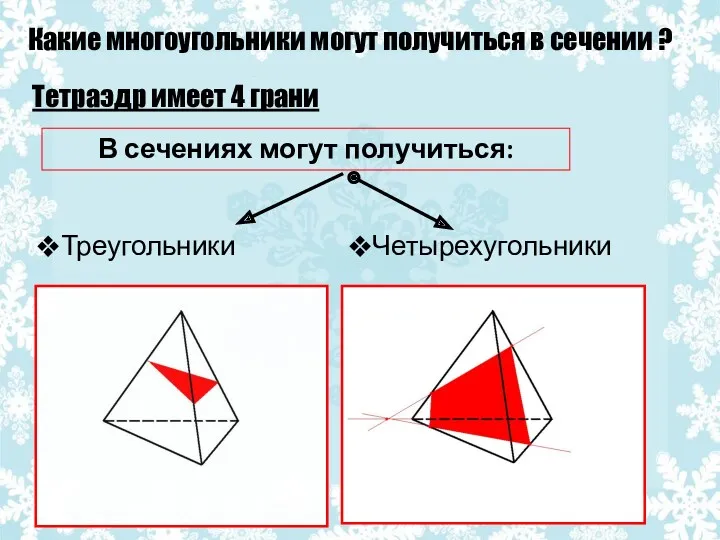
- 25. Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Четырехугольники
- 26. 1. Соединять можно только две точки, лежащие в плоскости одной грани. Для построения сечения нужно построить
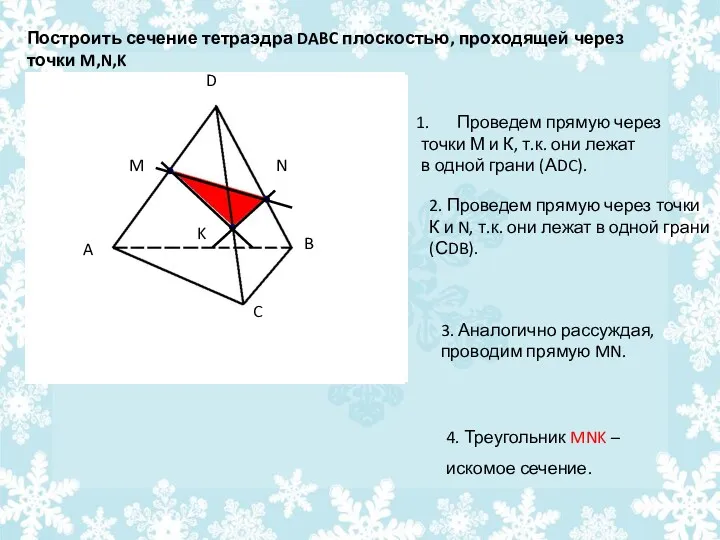
- 27. Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Проведем прямую через точки М и К,
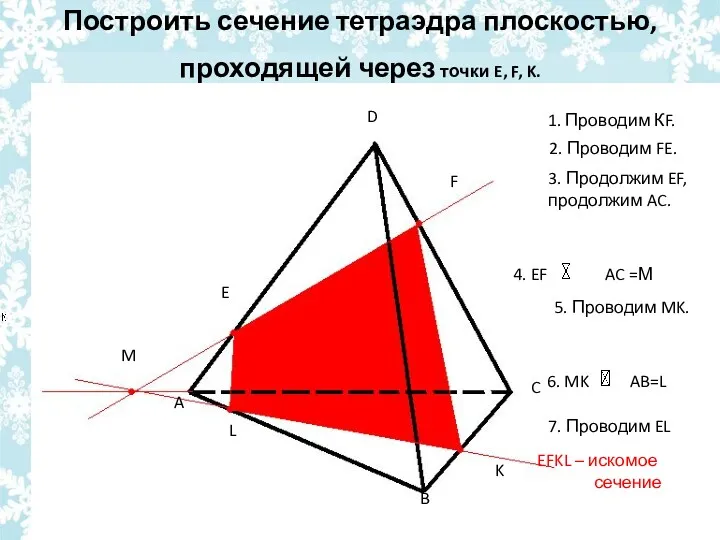
- 28. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. E F K L A B
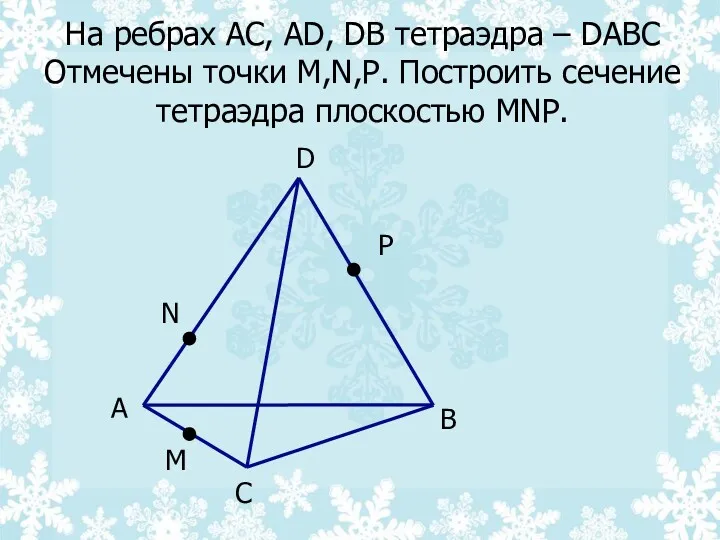
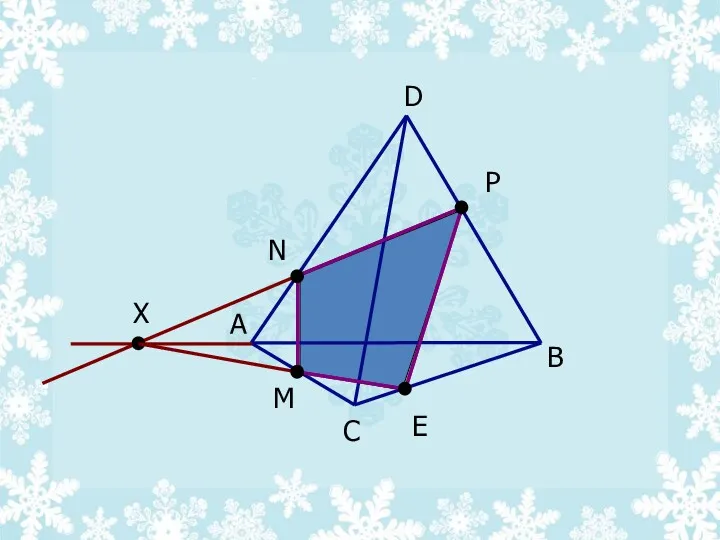
- 29. На ребрах AC, AD, DB тетраэдра – DABC Отмечены точки M,N,P. Построить сечение тетраэдра плоскостью MNP.
- 30. А C D B M N P Х E
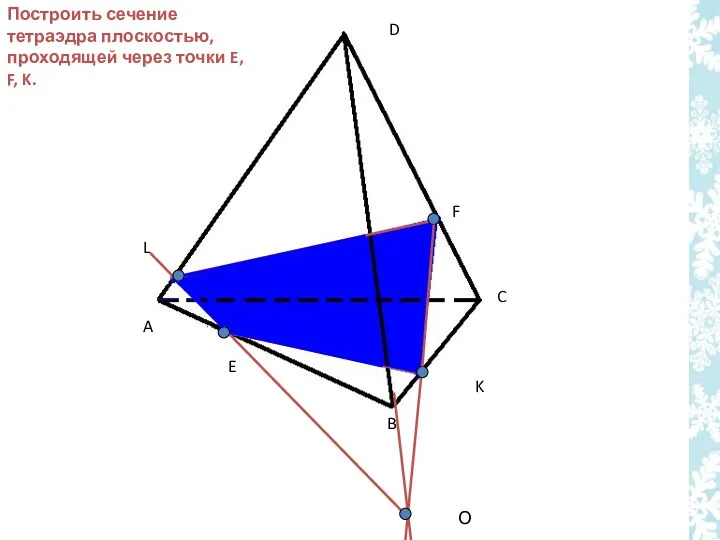
- 31. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. E F K L A B
- 32. E F L A B C D О Построить сечение тетраэдра плоскостью, проходящей через точки E,
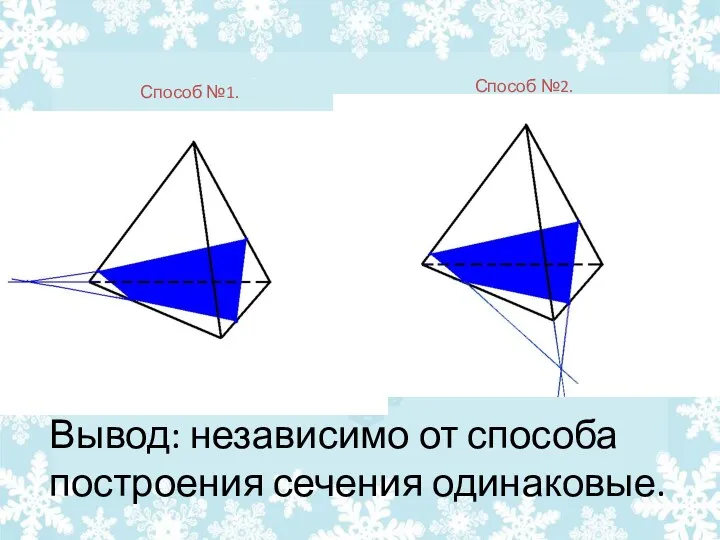
- 33. Вывод: независимо от способа построения сечения одинаковые. Способ №1. Способ №2.
- 35. Скачать презентацию

















 Публичная презентация результатов педагогической деятельности и инновационной работы учителя математики
Публичная презентация результатов педагогической деятельности и инновационной работы учителя математики Решение задач на движение
Решение задач на движение Статистическое моделирование
Статистическое моделирование Методы параметрического спектрального анализа. Введение
Методы параметрического спектрального анализа. Введение Фигуры: плоские и объёмные
Фигуры: плоские и объёмные Общая теория. Графики. Тренажер
Общая теория. Графики. Тренажер Урок математики в 4 классе. Сквозной урок: математика и сказки Пушкина.
Урок математики в 4 классе. Сквозной урок: математика и сказки Пушкина. Урок математики Арифметические действия над числами
Урок математики Арифметические действия над числами Геометричні перетворення
Геометричні перетворення Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Проверка статистической гипотезы
Проверка статистической гипотезы презентация к уроку Распределительное свойство умножения
презентация к уроку Распределительное свойство умножения Рациональные числа. Математический диктант
Рациональные числа. Математический диктант Решение неравенств методом интервалов
Решение неравенств методом интервалов Решение задач в 2 действия
Решение задач в 2 действия Возведение целых чисел в степень с натуральным показателем
Возведение целых чисел в степень с натуральным показателем Трехзначные числа
Трехзначные числа Своя игра. Интеллектуальная математическая игра. (6 класс)
Своя игра. Интеллектуальная математическая игра. (6 класс) Тест по теме: Аксиомы стереометрии и некоторые следствия из них
Тест по теме: Аксиомы стереометрии и некоторые следствия из них Мультимедийная разработка учебного занятия. Параллелограмм
Мультимедийная разработка учебного занятия. Параллелограмм Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100.
Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100. Отношения между множествами
Отношения между множествами Мастер- класс по математике Создание проблемной ситуации на уроках математики, как средство развития творческого мышления младших школьников
Мастер- класс по математике Создание проблемной ситуации на уроках математики, как средство развития творческого мышления младших школьников Тригонометриялық функциялардың қосындысын және айырмасын көбейтіндіге түрлендіру формулалары
Тригонометриялық функциялардың қосындысын және айырмасын көбейтіндіге түрлендіру формулалары Морской бой. Правила игры. Тема: Математика
Морской бой. Правила игры. Тема: Математика Приближенное решение нелинейных уравнений. Метод хорд
Приближенное решение нелинейных уравнений. Метод хорд Презентация к уроку математики в 1 классе по теме Многоугольники по программе Начальная школа ХХI века
Презентация к уроку математики в 1 классе по теме Многоугольники по программе Начальная школа ХХI века Презентация к занятиюФея математики
Презентация к занятиюФея математики