Содержание
- 2. 2 sin2 x + 3 sin x – 2 = 0 2 sin2 x – 5
- 3. 2 sin2 x + 3 sin x – 2 = 0 a · x 2 +
- 4. 2 sin2 x + 3 sin x – 2 = 0 Пусть sin x = t
- 5. 2 sin2 x + 3 sin x – 2 = 0 ? Если в уравнении встречаются
- 6. -2 cos2x – 5 cosx – 3 = 0 2 sin2 x – 5 cos x
- 7. ? Если в уравнении встречаются разные тригонометрические функции, то надо попытаться их заменить на какую-нибудь одну,
- 8. tg x + 3 ctg x – 4 = 0 tg x · ctg x =
- 9. ? Уравнение решается путём деления обеих его частей на старшую степень косинуса, то есть на cos
- 10. 4 sin x + 3 cos x = 0 l : cos x ≠ 0 4
- 11. ? Уравнение решается путём деления обеих его частей на старшую степень косинуса, то есть на cos
- 12. sin2 x - 5 sin x · cos x + 6 cos2 x = 0 l
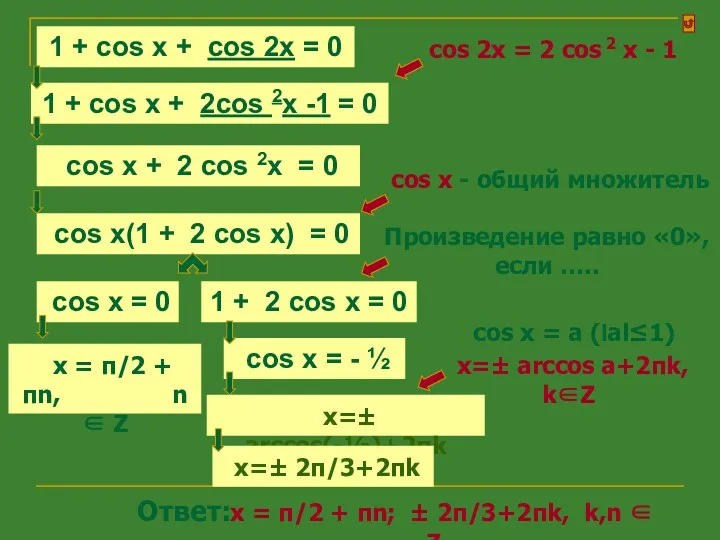
- 13. 1 + cos x + cos 2x = 0 ? Это уравнение решается c помощью одной
- 14. x=± arccos(-½)+2πk 1 + cos x + cos 2x = 0 cos 2x = 2 cos
- 15. cos x + sin 2x = 0 ? Это уравнение решается c помощью формулы тригонометрии: sin
- 16. x=(-1)k·arcsin½+πk cos x - 2 sin x · cos x = 0 cos x(1 - 2
- 17. ? Это уравнение решается путём вынесения общего множителя за скобки В результате разность тригонометрических функций преобразуется
- 18. x=arctg √3+πk tg x (√3 · tg x – 3) = 0 tg x - общий
- 19. 4 cos2 x - 1 = 0 ? Это уравнение решается путём разложения выражения на множители
- 21. Скачать презентацию
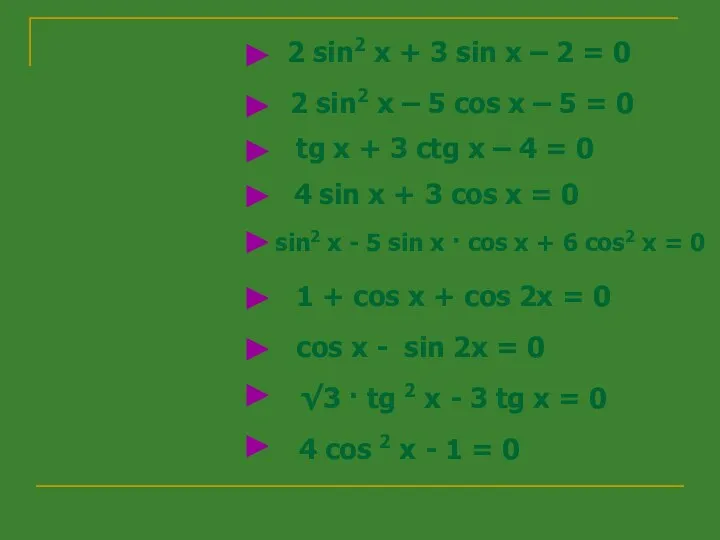
















 Применение производной и интегралов в различных областях биологии и химии
Применение производной и интегралов в различных областях биологии и химии Теорема Пифагора
Теорема Пифагора Самостоятельная работа
Самостоятельная работа Түзусызықты теңайнымалы қозғалыс, үдеу
Түзусызықты теңайнымалы қозғалыс, үдеу Из истории геометрических терминов
Из истории геометрических терминов Презентация Сочетательное свойство сложения
Презентация Сочетательное свойство сложения Решение задач на смеси и сплавы
Решение задач на смеси и сплавы Интеллектуальные информационные системы. Лекция 6. Нечеткая логика. Математические основы
Интеллектуальные информационные системы. Лекция 6. Нечеткая логика. Математические основы Решение задач по теме Параллельность плоскостей. Тетраэдр и параллелепипед
Решение задач по теме Параллельность плоскостей. Тетраэдр и параллелепипед Повторення вивченого. Додаткові вправи. Урок №136
Повторення вивченого. Додаткові вправи. Урок №136 Игра – самый умный математик. 6 класс
Игра – самый умный математик. 6 класс Расстояние между двумя точками. Масштаб
Расстояние между двумя точками. Масштаб Таблица истинности для импликации
Таблица истинности для импликации Нестандартные способы решения тригонометрических уравнений
Нестандартные способы решения тригонометрических уравнений Площади параллелограмма, треугольника и трапеции. Урок 21-22
Площади параллелограмма, треугольника и трапеции. Урок 21-22 Графоаналитические методы оценки параметров распределения (лекция 5)
Графоаналитические методы оценки параметров распределения (лекция 5) Додавання і віднімання раціональних чисел
Додавання і віднімання раціональних чисел П’єр де Ферма (1601-1665)
П’єр де Ферма (1601-1665) Презентация к уроку Задача 1 класс
Презентация к уроку Задача 1 класс Рішення рівнянь
Рішення рівнянь Делители и кратные (часть 3)
Делители и кратные (часть 3) Тест по теме: четырехугольники
Тест по теме: четырехугольники Решение систем линейных уравнений методом Крамера, методом Гаусса и матричным методом (вопросы)
Решение систем линейных уравнений методом Крамера, методом Гаусса и матричным методом (вопросы) Дроби. Нахождение части числа. Нахождение целого по его части.
Дроби. Нахождение части числа. Нахождение целого по его части. Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел Меньше или больше. Демонстрационный материал. 5 класс
Меньше или больше. Демонстрационный материал. 5 класс ПРЕЗЕНТАЦИЯ Умножение многозначного числа на однозначное (закрепление)
ПРЕЗЕНТАЦИЯ Умножение многозначного числа на однозначное (закрепление) Презентация ТАНГРАМ Животные
Презентация ТАНГРАМ Животные