Интеллектуальные информационные системы. Лекция 6. Нечеткая логика. Математические основы презентация
Содержание
- 2. Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств
- 3. ? Для поддержки принятия решений в медицине и экономике. ? В автомобильной, аэрокосмической и транспортной промышленности,
- 4. Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x) – степень принадлежности к нечеткому
- 5. Формализуем неточное определение 'горячий чай'. В качестве x (область рассуждений) будет выступать шкала температуры в градусах
- 6. Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов,
- 7. В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в
- 8. Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных. Нечеткая переменная описывается набором (N,X,A), где
- 9. Каждая лингвистическая переменная состоит из: • Названия; • Множества своих значений, которое также называется базовым терм-множеством
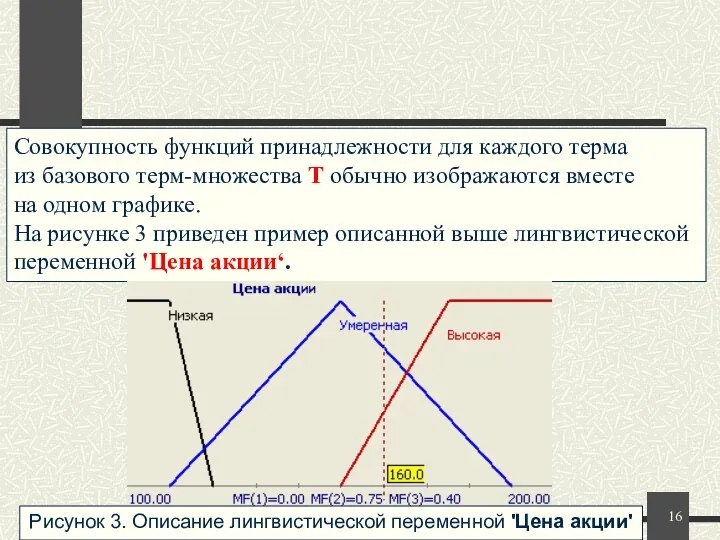
- 10. Рассмотрим нечеткое понятие 'Цена акции'. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество,
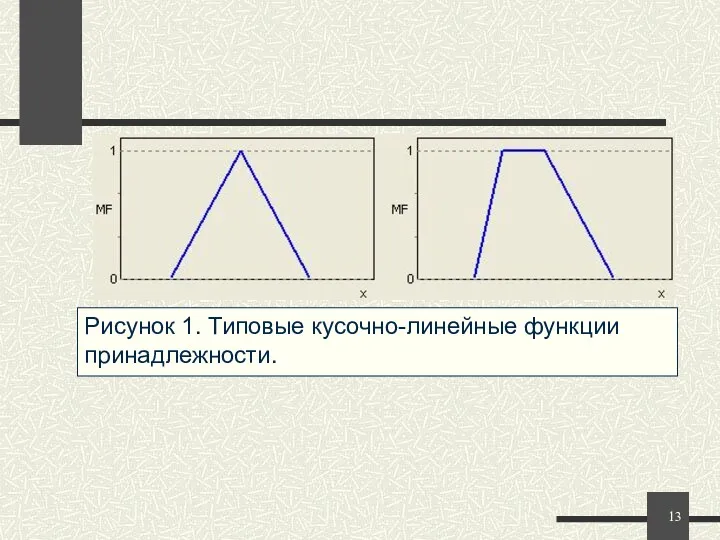
- 11. Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
- 12. Для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d): При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный
- 13. Рисунок 1. Типовые кусочно-линейные функции принадлежности. При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
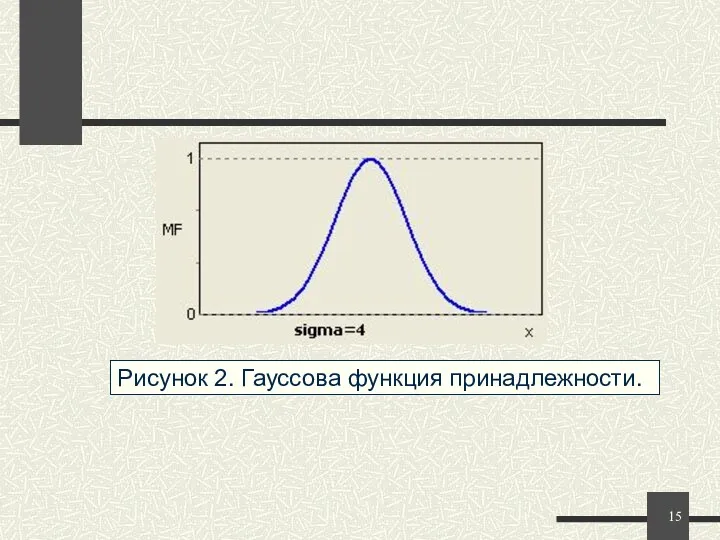
- 14. Функция принадлежности гауссова типа описывается формулой: и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества,
- 15. Рисунок 2. Гауссова функция принадлежности. При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
- 16. Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике.
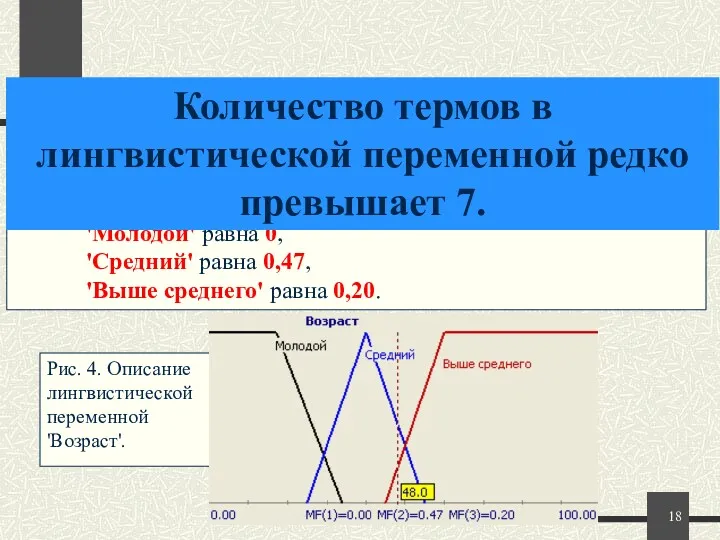
- 17. На рисунке 4 представлена формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности
- 18. На рисунке 4 представлена формализация неточного понятия 'Возраст человека'. Так, для человека 48 лет степень принадлежности
- 19. Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме 'Если-то'
- 20. Пусть в базе правил имеется m правил вида: R1: ЕСЛИ x1 это A11 … И …
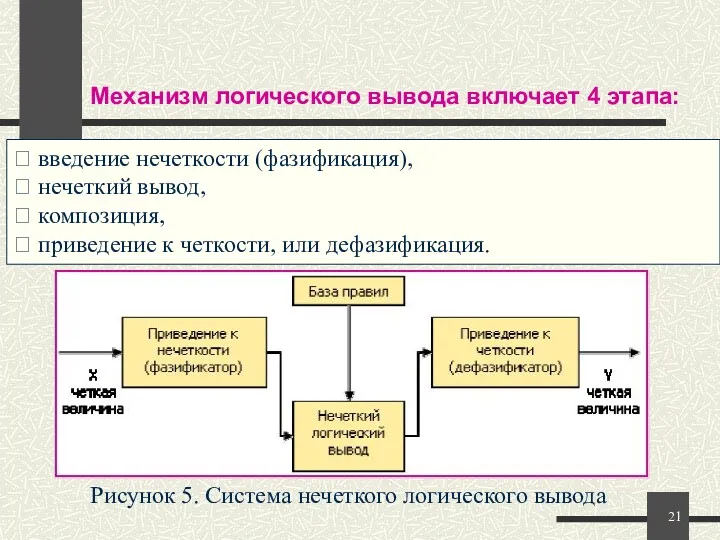
- 21. ? введение нечеткости (фазификация), ? нечеткий вывод, ? композиция, ? приведение к четкости, или дефазификация. Механизм
- 22. Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны
- 24. Скачать презентацию
















 математика. Тест
математика. Тест Таблицы. Компоненты действий.
Таблицы. Компоненты действий. Координатны вектора. Разложение вектора по координатным векторам
Координатны вектора. Разложение вектора по координатным векторам Координатная плоскость. Демонстрационный материал. 6 класс
Координатная плоскость. Демонстрационный материал. 6 класс Комплексные числа
Комплексные числа Введение в математический анализ
Введение в математический анализ Программа Живая геометрия
Программа Живая геометрия Аксонометрія. Метод паралельного проецирування
Аксонометрія. Метод паралельного проецирування Удивительная наука геометрия
Удивительная наука геометрия презентация к уроку по математике Единицы времени. Год
презентация к уроку по математике Единицы времени. Год состав числа 2 и 3
состав числа 2 и 3 КАЖДЫЙ ДЕНЬ ЖИЗНИ ПРИБАВЛЯЕТ ЧАСТИЧКУ МУДРОСТИ
КАЖДЫЙ ДЕНЬ ЖИЗНИ ПРИБАВЛЯЕТ ЧАСТИЧКУ МУДРОСТИ Итоговый тест по математике. 5 класс
Итоговый тест по математике. 5 класс Нахождение числа по заданному значению его дроби. Правило нахождения числа по его дроби
Нахождение числа по заданному значению его дроби. Правило нахождения числа по его дроби Решение задач
Решение задач Особенности работы со слабоуспевающими обучающимися на уроках математики
Особенности работы со слабоуспевающими обучающимися на уроках математики Миллиметр. 2 класс
Миллиметр. 2 класс
 Дифференциальные уравнения
Дифференциальные уравнения Диагонали четырёхугольников
Диагонали четырёхугольников Последовательности. Формирование понятия последовательности
Последовательности. Формирование понятия последовательности Внеклассное мероприятие по математике Своя игра (для учащихся 5-х классов)
Внеклассное мероприятие по математике Своя игра (для учащихся 5-х классов) Проверка статистических гипотез. (Лекция 4)
Проверка статистических гипотез. (Лекция 4) Нормальный закон распределения. (Тема 6)
Нормальный закон распределения. (Тема 6) Дробные рациональные уравнения
Дробные рациональные уравнения Пьер Ферма (1601-1665)
Пьер Ферма (1601-1665) Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями