Содержание
- 2. Правила Уравнения называются ЦЕЛЫМИ, если у них левая и правая части являются целыми выражениями (т.е. не
- 3. Устно №265
- 4. Надо научиться решать уравнения n-й степени Рn(х)=0 При n=1 имеем линейное уравнение ax +b=0? у которого
- 5. Уравнение n-й степени Рn(х)=0 имеет не более n корней Для 3-й и 4-й степени существуют формулы
- 6. КАК РЕШАТЬ? ?
- 7. Разложение на множители Замена переменной Графический способ Три основных приёма:
- 8. Пример1. х³+2x²-x-2=0 x²(х+2) – (х+2)=0 (х+2)(x²-1)=0 (х+2)(х-1)(х+1)=0 х=-2; х=-1; х=1
- 9. Пример2. 6х²(x-1)-x²+x-2x+=0 6х²(x-1)-(х²-x)-(2х-2)=0 6х²(x-1)-х(х-1)-2(х-1)=0 (х-1)(6х²-x-2)=0 х=1; х=2/3; х=-1/2
- 10. Кубическое уравнение – алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ax³+bx²+cx+d=0, где a≠0 Заменяя в
- 11. Решение кубического уравнения можно получить с помощью формулы Кардано: Если Если >0, то кубическое уравнение имеет
- 12. Биквадратное уравнение ах +bx²+c=0 4 Решаются заменой переменной у=х² ау²+by+c=0
- 13. Пример3. 4х - 5х² + 1=0 у=х² 4у²-5у+1=0 у=1; у=1/4 х=-1; х=1; х=1/2; х=-1/2 4
- 14. Пример4. (х²-2x)²-4(x²-2x)+3=0 у=(x²-2x) у²-4у+3=0 у=1; у=3 х²-2х=1 х²-2х=3 х²-2х-1=0 х²-2х-3=0 х=1-√2; х=1+√2; х=-1; х=3
- 15. Пример5. (х²+4х+3)(х²+4х+1)=48 у= (х²+4х+1) у(у+2)=48 у²+2у-48=0 у=-8 у=6 х²+4х+1=-8 х²+4х+1=6 х²+4х+9=0 х²+4х-5=0 корней нет х=-5; х=1
- 16. Пример 6. (х-1)(х+1)(х+3)(х+5)=105 При решении этой задачи важно сообразить, что (х-1)(х+5)=х²+4x-5, (х+1)(х+3)= х²+4x+3. Поэтому изменив порядок
- 17. Пример 7. (х²+3x-8)²+2x(х²+3x-8)-3х²=0 Многочлен, который стоит в левой части уравнения, легко свести к однородному многочлену двух
- 18. y²+2xy-3x²=0 D= у= у= у=-3х и у=х.
- 19. Возвращаясь к переменной х, имеем два уравнения: х²+3x-8=-3х и х²+3x-8=х (корни х=-3- √17 и х=-3+ √17)
- 20. Решите уравнение: №272(а) y³-6y=0 y(y²-6)=0 Ответ: у=0, у=-√6, y=√6
- 21. Решите уравнение: №272(д) 9х³-18x²-x+2=0 (9х³-18x²)-(x-2)=0 9x²(х-2)-(x-2)=0 (x-2)(9x²-1)=0 (x-2)(3х-1)(3х+1)=0 Ответ: х=-1/3, х=1/3, х=2
- 22. Решите уравнение: №276(а) (2х² +3)² – 12(2х²+3)+11=0 Заменим (2х²+3)=h, имеем h²-12h+1=0
- 23. Решите уравнение: №278(а) х – 5х² -36=0 4
- 24. Теорема Безу.
- 25. Преподавал математику в Училище гардемаринов (1763) и Королевском артиллерийском корпусе (1768). Основные его работы относятся к
- 26. Любой многочлен R(x) можно представить в виде: P(x)= (х-а) ∙Q(х) + r, где r =P(a) Пример
- 27. Теорема Безу. Если уравнение а х + a x + … + a x+a = 0,
- 28. х³-8х²+19х-12=0 Свободный член – 12 имеет делители ±1, ±2, ± 3, ±4, ±6, ±12. При x=1
- 29. Решение задач. 1) Решить уравнения: а) х³-3х²-4х+12=0, б) х³+4х²+5х+2=0, в) х +4х³+х²-12х-12=0, г) х +4х³-х²-16х-12=0. 4
- 30. Решим уравнение с помощью теоремы Безу: х³-6х²+11х-6=0
- 31. Можно не делить многочлен на двучлен, а воспользоваться схемой Горнера Метод назван в честь Уильяма Джоржа
- 32. Решить уравнение: х³-5х+4=0 х³-3х+2=0 4: на +/-1;+/-2; +/-4 х³-5х+4=(х-1)(х²+х-4)=0
- 33. Возвратные уравнения Рассмотрим уравнения: x³-3x²-3x+1=0 3х -7х³+x²-7x+3=0 -х³+5x²+5x-1=0 Все три уравнения объединяет то, что коэффициенты равноотстоящие
- 34. КАК РЕШАТЬ? ?
- 35. Рассмотрим методы решения возвратных уравнений 3-ей и 4-ой степени. В общем виде возвратное уравнение 3-ей степени
- 36. Тогда уравнение (3) примет вид полученное уравнение равносильно совокупности двух уравнений , , решая первое уравнение
- 37. Рассмотрим возвратное уравнение 4-ой степени (4) Так как , то не является корнем этого уравнения. Поэтому,
- 38. Полученное уравнение можно решить уже знакомым нам методом замены переменной. Пусть ,тогда ,откуда получаем, что и
- 39. Решив это уравнение, найдем его корни t1и t2 Теперь чтобы найти корни уравнения (4) необходимо решить
- 40. Решение. Имеем возвратное уравнение 4-ой степени. Разделим обе части уравнения на х², проведем группировку слагаемых и
- 41. Решая это уравнение, получим и Для нахождения корней первоначального уравнения решим дробно-рациональные уравнения решение которых сводится
- 42. Решить уравнения: 5х³-4x²-4x+5=0
- 43. Решить уравнения: 2x -5x³+4x²-5x+2=0 4
- 44. Однородные уравнения Одноро́дным уравнением n-й степени, называется дифференциальное уравнение вида: Такое уравнение заменой сводится к алгебраическому
- 45. Примеры однородных уравнений: sin х — cos х = 0, 3(х²+5)²+4(х²+5)(х-7)-7(х-7)²=0 (х-3)+4(х+3)=5(х²-9)² ↔ (х-3)+4(х+3)=5(х-3)²(х+3)² 4 4
- 46. КАК РЕШАТЬ? ?
- 47. (х-3)+4(х+3)=5(х-3)²(х+3)² Разделим обе части уравнения на (х-3) и сделаем замену t=((х+3):(х-3))² Получим равносильное уравнение: 1+4t²=5t, корни
- 48. Итоги урока: Какие уравнения называются уравнениями высоких порядков? Что значит решить уравнение? Сколько корней может иметь
- 50. Скачать презентацию











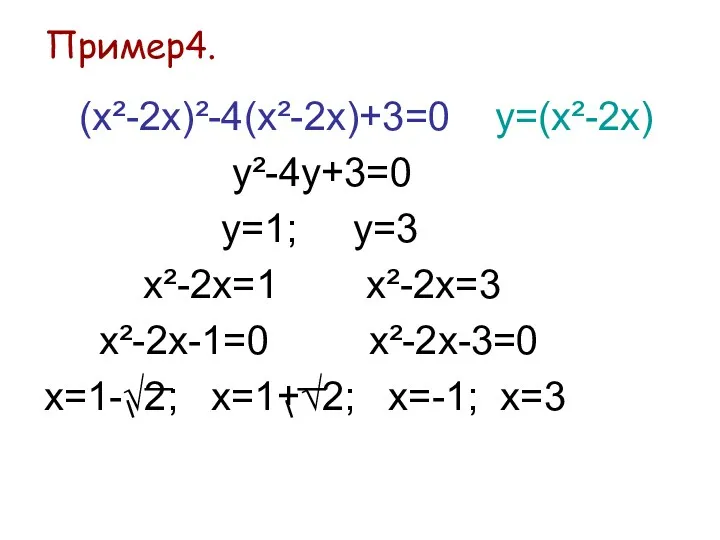



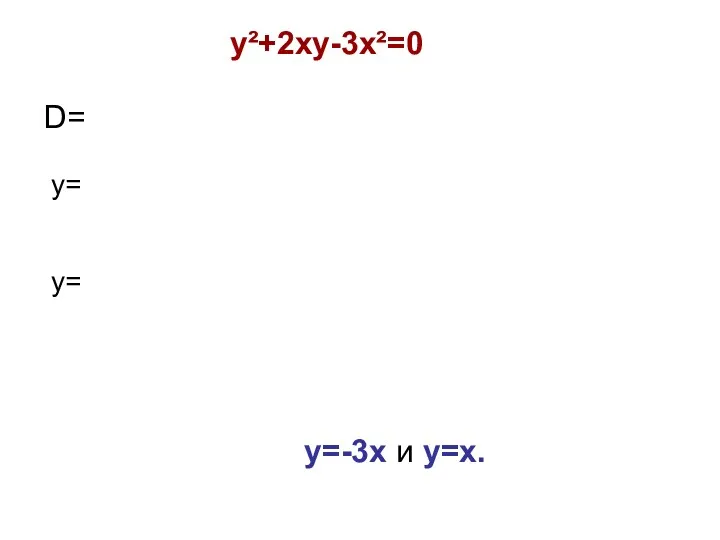





























 Исследование функций. Чтение графика
Исследование функций. Чтение графика Понятие движения
Понятие движения Устный счет
Устный счет Математика вокруг нас
Математика вокруг нас Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Деление степеней
Деление степеней Час занимательной математики Заниматика
Час занимательной математики Заниматика Преобразование графиков функции
Преобразование графиков функции Теорема Пифагор
Теорема Пифагор Формы организации учебной деятельности на уроке решения задач
Формы организации учебной деятельности на уроке решения задач Признак возрастания (убывания) функции
Признак возрастания (убывания) функции конспект и презентация урока по математике 3 класс Квадратный метр
конспект и презентация урока по математике 3 класс Квадратный метр Задачи на деление
Задачи на деление Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Окружность и круг
Окружность и круг Статистическое изучение связи между явлениями
Статистическое изучение связи между явлениями Таблица сложения
Таблица сложения Пересечение поверхностей, одна из которых проецирующая. Пересечение полусферы и проецирующего цилиндра
Пересечение поверхностей, одна из которых проецирующая. Пересечение полусферы и проецирующего цилиндра Логарифмические уравнения
Логарифмические уравнения Презентация по математике. Таблица умножения на 8
Презентация по математике. Таблица умножения на 8 Декартові координати у просторі
Декартові координати у просторі Задачи на движение. Математика. 5 класс
Задачи на движение. Математика. 5 класс Свойства действий с рациональными числами. Часть 2
Свойства действий с рациональными числами. Часть 2 Вычитание дробей с одинаковыми знаменателями
Вычитание дробей с одинаковыми знаменателями Урок математики 2 класс. Перспектива. Сложение круглых десятков с однозначными числами.
Урок математики 2 класс. Перспектива. Сложение круглых десятков с однозначными числами. Неравенства. Тест
Неравенства. Тест Презентация к уроку математики Деление с остатком
Презентация к уроку математики Деление с остатком Число Пи
Число Пи