Слайд 2

§9. Уравнения в полных дифференциалах
Уравнение M(x , y)dx + N(x , y)dy = 0 (14)
называется уравнением в полных дифференциалах, если
его левая часть является полным дифференциалом некоторой функции u(x , y) , т.е. если
M(x , y)dx + N(x , y)dy = du(x , y) .
Общий интеграл уравнения в полных дифференциалах имеет вид u(x , y) = C .
⇒ Задачи:
1) научиться определять, когда выражение
M(x , y)dx + N(x , y)dy
является полным дифференциалом;
2) научиться находить функцию u(x , y), зная ее полный диф-
ференциал.
Слайд 3

ТЕОРЕМА 1.
Пусть функции M(x , y) , N(x , y) определены и непрерывны в области
D плоскости xOy и имеют в ней непрерывные частные производные
Для того чтобы выражение
M(x , y)dx + N(x , y)dy
представляло собой полный дифференциал некоторой функции u(x , y) , необходимо и достаточно, чтобы во всех точках области D выполнялось условие
ДОКАЗАТЕЛЬСТВО
Слайд 4

Способы нахождения функции u(x , y):
1) используя алгоритм, предложенный в доказательстве теоре-
мы 1;
2)
используя одну из следующих формул:
где (x0 ,y0) – любая точка области D непрерывности функций M(x , y), N(x , y).
Слайд 5

3) методом интегрируемых комбинаций.
Суть метода интегрируемых комбинаций: выделить в
M(x , y)dx + N(x , y)dy
выражения,
являющиеся дифференциалами известных функ-
ций («интегрируемые комбинации») и привести его таким образом к виду du(x , y) .
ПРИМЕРЫ интегрируемых комбинаций:
Слайд 6

§10. Интегрирующий множитель
Функция μ(x,y) называется интегрирующим множителем уравнения M(x , y)dx + N(x , y)dy = 0, (14)
если
после его умножения на μ(x,y) левая часть уравнения становится полным дифференциалом некоторой функции.
Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D плоскости xOy и имеют в ней непрерывные частные производные
Слайд 7

ТЕОРЕМА 1 (о существовании интегрирующего множителя вида μ(x) или μ(y)).
Пусть
1) Если
ϕ = ϕ(x), то уравнение (14) имеет интегрирующий множитель μ(x), который является решением уравнения
2) Если ψ = ψ(y), то уравнение (14) имеет интегрирующий множитель μ(y), который является решением уравнения






 Тренажёр Кот в сапогах (Математика, 1 класс)
Тренажёр Кот в сапогах (Математика, 1 класс) Круговые диаграммы
Круговые диаграммы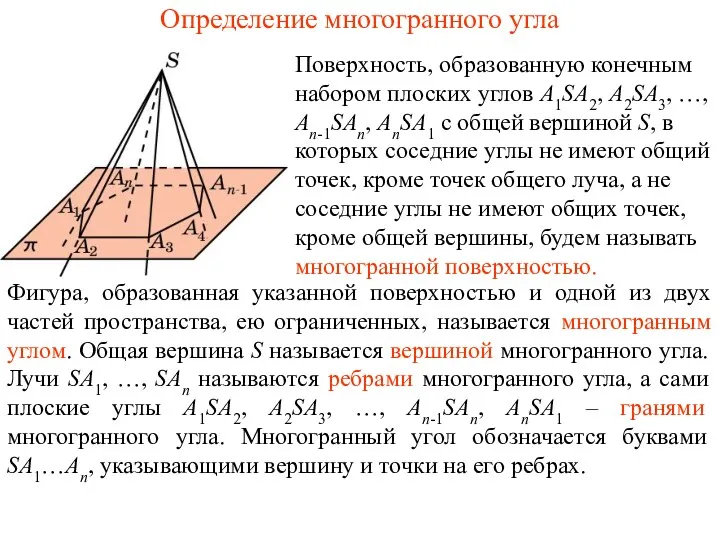 Определение многогранного угла
Определение многогранного угла Математические методы моделирования информационных процессов и систем. (Лекция 2)
Математические методы моделирования информационных процессов и систем. (Лекция 2) Дроби и проценты. Сложение и вычитание дробей
Дроби и проценты. Сложение и вычитание дробей Меры длины. Закрепление.
Меры длины. Закрепление. Отличный шанс
Отличный шанс Математика. Мы с логикой на ТЫ!
Математика. Мы с логикой на ТЫ! Метод подстановки
Метод подстановки Элементы теории ошибок измерений. Лекция №6
Элементы теории ошибок измерений. Лекция №6 Десятичные дроби. Математика и экология (часть 1)
Десятичные дроби. Математика и экология (часть 1) Число и цифра 5. Состав Числа 5.
Число и цифра 5. Состав Числа 5. Урок математики в 3 классе по теме:Окружность.Круг. Технологическая карта урока.
Урок математики в 3 классе по теме:Окружность.Круг. Технологическая карта урока. Келісім белгісі.Келісім белгісін қолданудың тәжірибелік үлгісі (Мендель заңы)
Келісім белгісі.Келісім белгісін қолданудың тәжірибелік үлгісі (Мендель заңы) Измерение отрезков
Измерение отрезков Взаимно обратные числа
Взаимно обратные числа Определение арифметической и геометрической прогрессий
Определение арифметической и геометрической прогрессий Общие сведения о кривых линиях и поверхностях
Общие сведения о кривых линиях и поверхностях презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5,
презентация к уроку математики Цифра 1 и чичла 1, 2, 3, 4, 5, Лас су желісі
Лас су желісі Основные понятия и определения. Предмет и основные вопросы метрологии. Физические свойства, величины, шкалы
Основные понятия и определения. Предмет и основные вопросы метрологии. Физические свойства, величины, шкалы Основи теорії ймовірності та математичної статистики. (Тема 1)
Основи теорії ймовірності та математичної статистики. (Тема 1) Аксиомы стереометрии. Геометрия. 10 класс
Аксиомы стереометрии. Геометрия. 10 класс Деление десятичной дроби на десятичную дробь. 5 класс
Деление десятичной дроби на десятичную дробь. 5 класс Аргументация и логическая прагматика
Аргументация и логическая прагматика Тренажёр счёта
Тренажёр счёта Измерительные шкалы
Измерительные шкалы Урок математики 2 класс
Урок математики 2 класс