Содержание
- 2. Пусть А – невырожденная (det A≠0) квадратная матрица (1.2) порядка n. Е – единичная матрица того
- 3. Теорема. ( О существовании обратной матрицы). Матрица А имеет обратную тогда и только тогда, когда ее
- 4. Теорема. Всякая невырожденная матрица имеет единственную обратную матрицу: Aij – алгебраическое дополнение элемента aij.
- 5. Δ≠0. Обратная матрица: n =2.
- 6. Обратная матрица: n = 3.
- 8. Пример Найти обратную матрицу к матрице Решение
- 9. Пример Найти обратную матрицу к матрице Решение
- 10. Пример Найти обратную матрицу к матрице Решение
- 11. Пример Найти обратную матрицу к матрице Решение
- 12. Пример Найти обратную матрицу к матрице Решение
- 13. Пример Найти обратную матрицу к матрице Решение
- 14. Пример Найти обратную матрицу к матрице Решение
- 15. Пример Найти обратную матрицу к матрице Решение
- 16. Пример Найти обратную матрицу к матрице Решение
- 17. Пример Найти обратную матрицу к матрице Решение
- 18. 4. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
- 19. К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи (по некоторым оценкам более 75% всех
- 20. Системой линейных алгебраических уравнений, содержащей т уравнений и n неизвестных, называется система вида (2.1) где x1,
- 21. Решением системы (2.1) будем называть упорядоченный набор чисел x1, x2, …, xn , обращающий каждое ее
- 22. (2.3)
- 23. Решить систему — значит найти все ее решения или доказать, что решений нет.
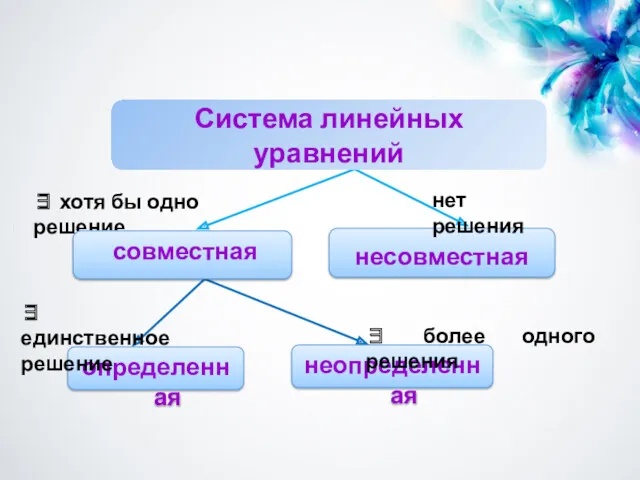
- 24. несовместная определенная неопределенная ∃ более одного решения ∃ единственное решение нет решения ∃ хотя бы одно
- 25. В случае неопределенной СЛАУ каждое ее решение называется частным решением. Совокупность всех частных решений называется общим
- 26. Система, у которой все свободные члены равны нулю (b1 = b2 =…= bn = 0), называется
- 27. Если число уравнений системы совпадает с числом неизвестных (m=n), то система называется квадратной. Если определитель матрицы
- 28. 4.1. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ РЕШЕНИЯ СЛАУ
- 29. Применение обратной матрицы для решения СЛАУ В матричной форме записи квадратная определенная система уравнений имеет вид:
- 30. Пример. Решить матричным способом систему уравнений Решение.
- 31. 4.2. Метод Крамера
- 32. Габриэль Крамер швейцарский математик, один из создателей линейной алгебры (1704 -1752)
- 33. . (2.7) Метод Крамера Пусть квадратная определенная система в матричной форме имеет вид : АХ=В, det
- 34. Введем в рассмотрение следующие три определителя для матрицы системы (2.8): Теорема (правило Крамера). Если Δ ≠
- 35. : Cогласно (2.9), получаем Пример. Решить по правилу Крамера систему уравнений Решение. Вычислим определитель системы
- 37. Рассмотрим систему трех линейных уравнений с тремя неизвестными (2.10) n=3. Обозначим Вспомогательные определители Δ1, Δ2, Δ3
- 38. Теорема (правило Крамера). Если Δ ≠ 0, то система (2.10) имеет единственное решение, которое находится по
- 40. Скачать презентацию




































 Древний Египет и Междуречье и математика
Древний Египет и Междуречье и математика Понятие многогранника, призмы и их элементов
Понятие многогранника, призмы и их элементов Математичні методи в біології
Математичні методи в біології Презентация урока на тему: Таблица умножения и деления на 6. Закрепление. Урок-сказка.
Презентация урока на тему: Таблица умножения и деления на 6. Закрепление. Урок-сказка. Десятичные дроби и действия над ними
Десятичные дроби и действия над ними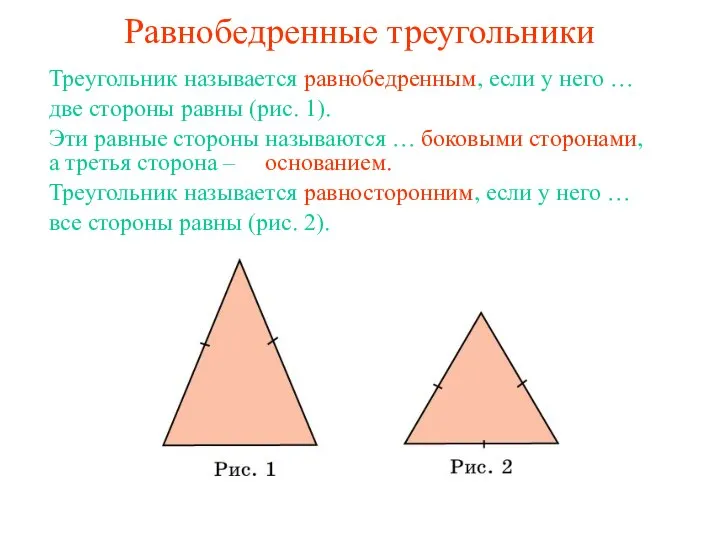 Равнобедренные треугольники
Равнобедренные треугольники ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку
ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку Метод Гаусса
Метод Гаусса Возможности и использование системы компьютерной математики Scilab. Тема 3
Возможности и использование системы компьютерной математики Scilab. Тема 3 Смысл действия умножения. Конкретный смысл действия деления. Табличное умножение
Смысл действия умножения. Конкретный смысл действия деления. Табличное умножение ПРЕЗЕНТАЦИЯ К ЗАНЯТИЮ ПО ФЭМП ДЛЯ 2 мл. гр. ЧАСТИ СУТОК
ПРЕЗЕНТАЦИЯ К ЗАНЯТИЮ ПО ФЭМП ДЛЯ 2 мл. гр. ЧАСТИ СУТОК Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Счастливый случай. Урок-игра. 6 класс
Счастливый случай. Урок-игра. 6 класс Числа, кратные 9
Числа, кратные 9 Увеличение и уменьшение числа в несколько раз
Увеличение и уменьшение числа в несколько раз презентация к уроку по математике в 1 классе
презентация к уроку по математике в 1 классе Случаи вычитания 13-
Случаи вычитания 13- Фигуры: плоские и объёмные
Фигуры: плоские и объёмные Урок по математике Единицы длины. Километр. 4 класс
Урок по математике Единицы длины. Километр. 4 класс Бенефис логарифмической функции
Бенефис логарифмической функции Возведение в степень произведения и степени
Возведение в степень произведения и степени Десятичные дроби. Задания для устного счета
Десятичные дроби. Задания для устного счета Равные множества.
Равные множества. Действия с десятичными дробями в коррекционной школе. 8 класс
Действия с десятичными дробями в коррекционной школе. 8 класс Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Сложение и вычитание положительных и отрицательных чисел. (6 класс)
Сложение и вычитание положительных и отрицательных чисел. (6 класс) Смешанные числа. Математический диктант
Смешанные числа. Математический диктант Методы и модели корреляционно-регрессионного анализа. Лекция 2
Методы и модели корреляционно-регрессионного анализа. Лекция 2