Содержание
- 2. Решение систем линейных уравнений. Метод Гаусса Пример.
- 3. 1) Составим расширенную матрицы системы
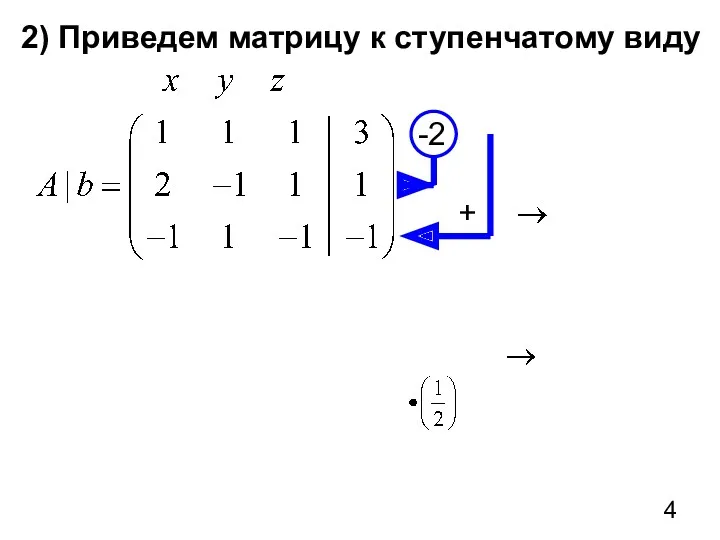
- 4. 2) Приведем матрицу к ступенчатому виду
- 6. 3) Составим новую систему Система имеет единственное решение Можно было продолжить преобразования, и привести систему к
- 7. Теорема Кронекера-Капелли.
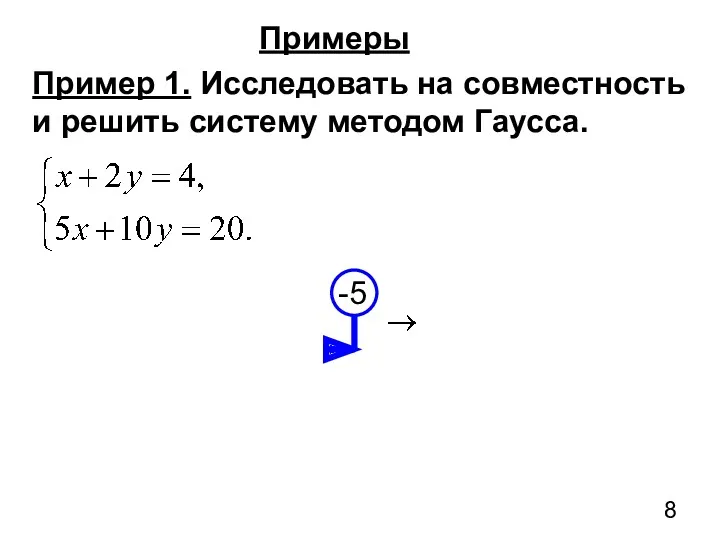
- 8. Примеры Пример 1. Исследовать на совместность и решить систему методом Гаусса.
- 9. Система имеет бесконечное множество решений. Найдем число свободных неизвестных
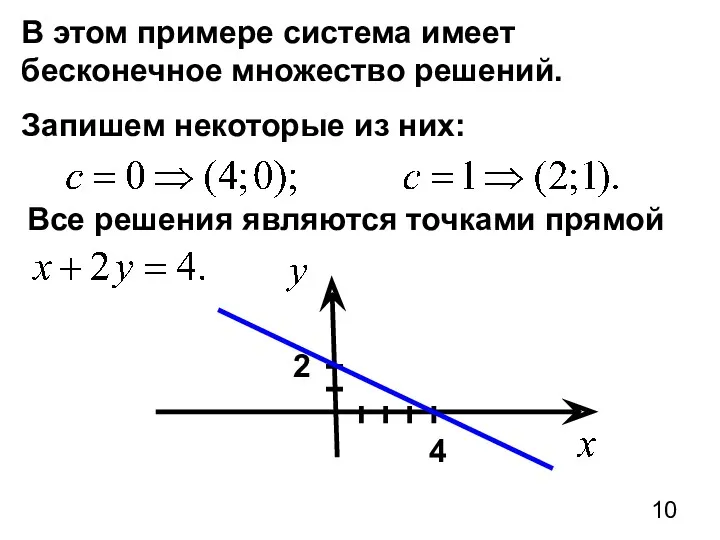
- 10. В этом примере система имеет бесконечное множество решений. Запишем некоторые из них:
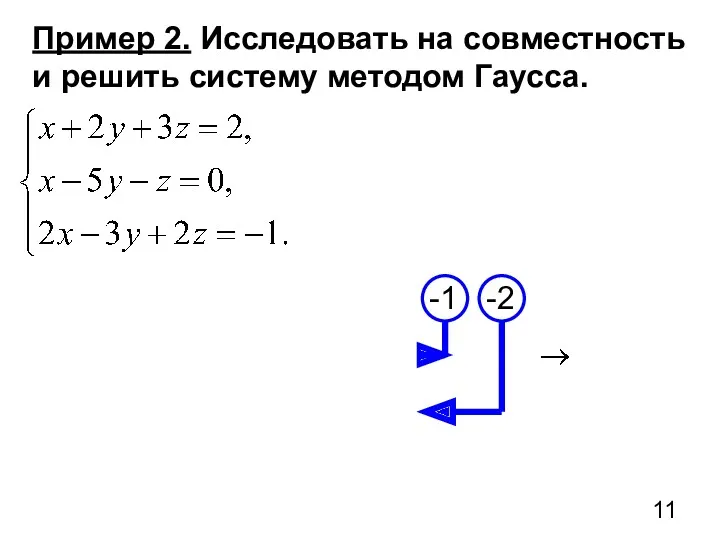
- 11. Пример 2. Исследовать на совместность и решить систему методом Гаусса.
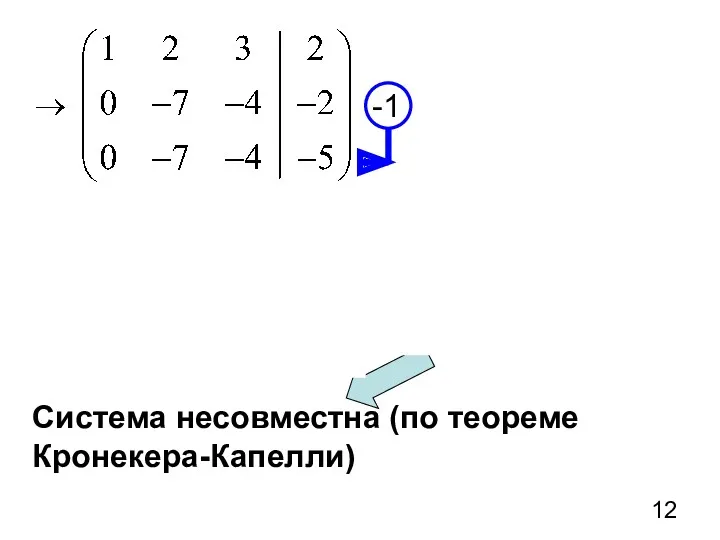
- 12. Система несовместна (по теореме Кронекера-Капелли)
- 13. Мы рассмотрели два метода решения систем линейных уравнений: 1) Метод Крамера 2) Метод Гаусса Метод Крамера
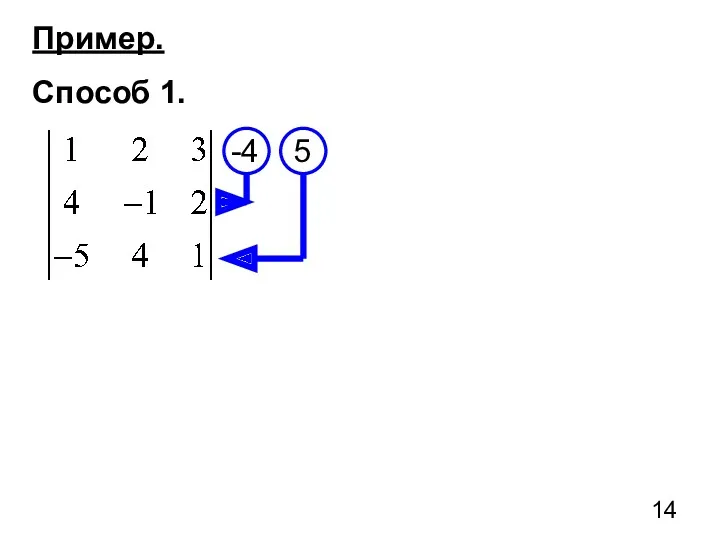
- 14. Пример. Способ 1. -4 5
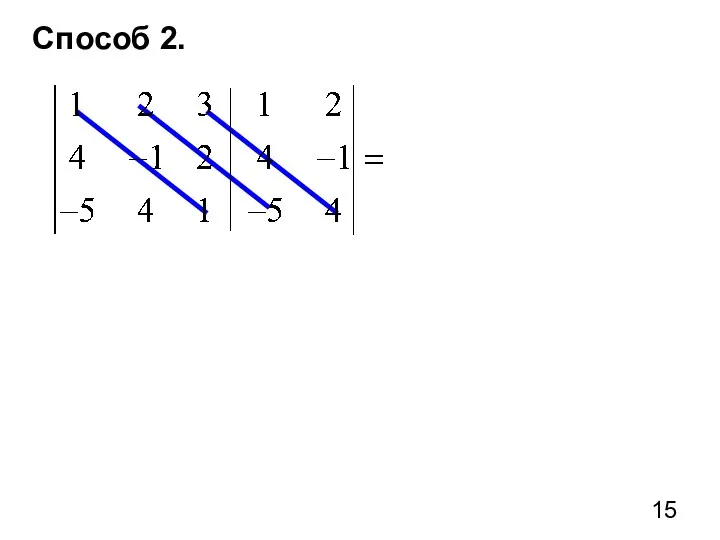
- 15. Способ 2.
- 16. 1) Определитель не изменится, если поменять строки на соответствующие столбцы Свойства определителей 2) Если у определителя
- 17. 4) Если две строки (столбца) поменять местами, то знак определителя изменится на противоположный. Свойства определителей 5)
- 18. Пример. Вычислить: (т.к. две одинаковые строки)
- 19. Пусть дана матрица Определителем второго порядка, соответствующим данной матрице, называется число Определитель обозначают символом
- 20. Таким образом, Числа называются элементами определителя Пример
- 21. Приведем свойства определителя второго порядка 1. Определитель не изменится, если его строки поменять местами с соответствующими
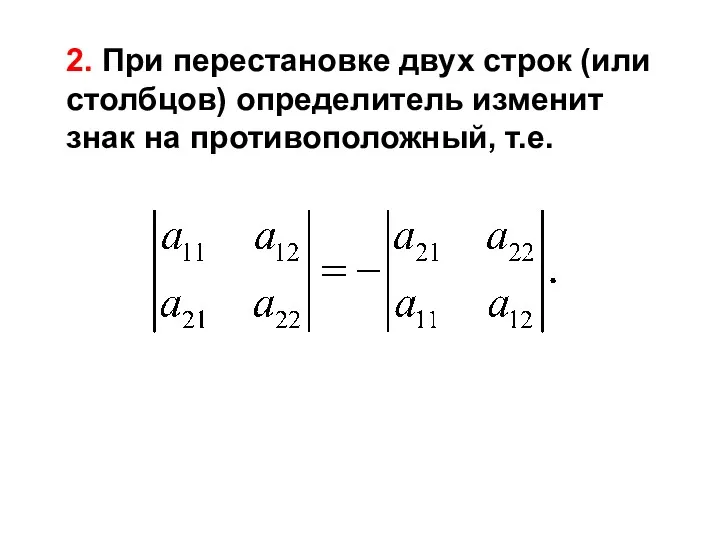
- 22. 2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, т.е.
- 23. 3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. 4. Общий множитель всех элементов строки
- 24. 5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю 6. Если к
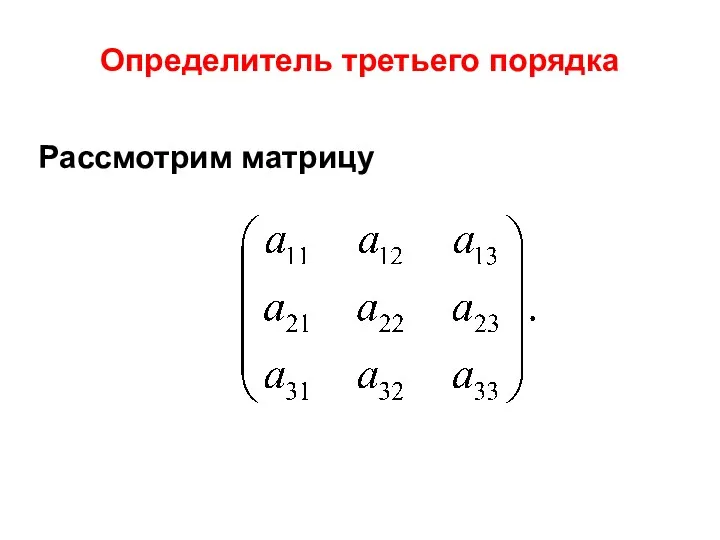
- 25. Рассмотрим матрицу Определитель третьего порядка
- 26. Определителем третьего порядка называют число
- 27. Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка, полученный из данного вычеркиванием строки
- 28. Назовем алгебраическим дополнением Например, Правило. Определитель третьего порядка равен сумме попарных произведений элементов какой-либо его строки
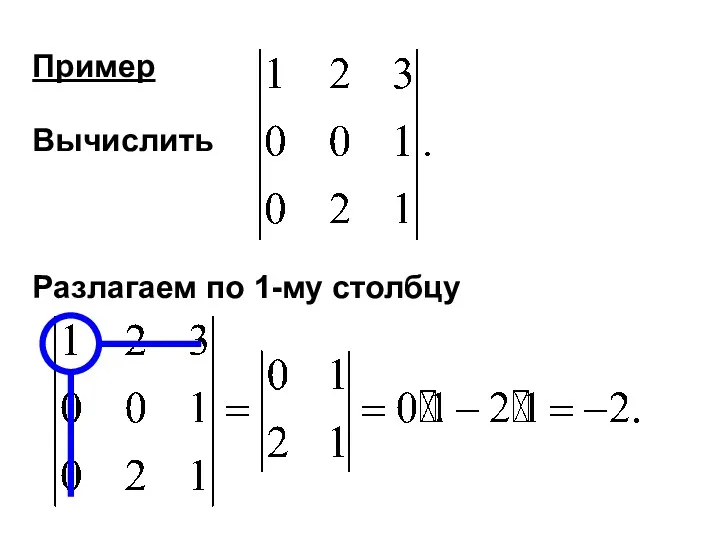
- 29. Пример Вычислить Разлагаем по 1-му столбцу
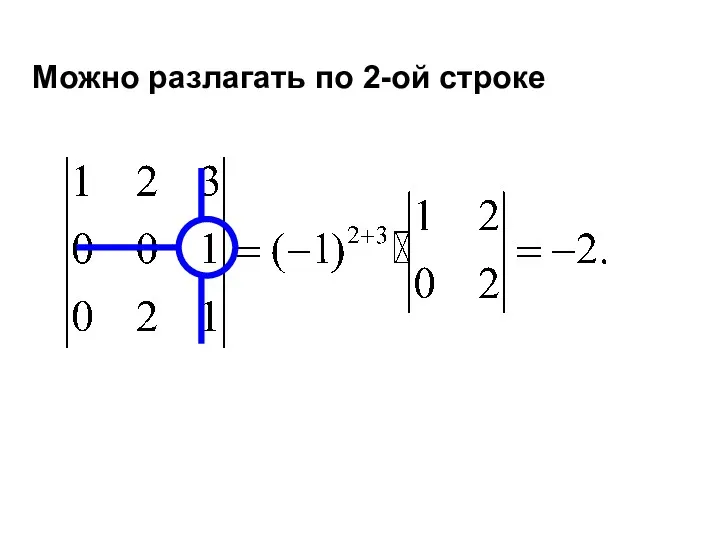
- 30. Можно разлагать по 2-ой строке
- 31. Все свойства определителей 2-ого порядка остаются справедливыми для определителей 3-его порядка. Свойства Пример Вычислить т.к. совпадают
- 32. Все свойства определителей 2-ого и 3-его порядков сохраняются для определителей высших порядков. Определители высших порядков Пример
- 33. Понятие обратной матрицы вводится только для квадратных матриц. Обратная матрица Опр. Матрица называется обратной к матрице
- 34. Теорема. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы матрица A была
- 35. Составим матрицу из алгебраических дополнений Составим новую матрицу поменяв местами строки и столбцы (матрица называется транспонированной).
- 37. Составим матрицу, обратную матрице второго порядка Здесь Тогда
- 38. Пример. то A – невырожденная, и, следовательно, существует обратная матрица
- 39. Вычисляем алгебраические дополнения:
- 42. Свойства Примеры Вычислить определитель произведения 1. 2.
- 43. По свойству 1
- 44. Домашнее задание 1. Проверить, что, действительно
- 46. Скачать презентацию


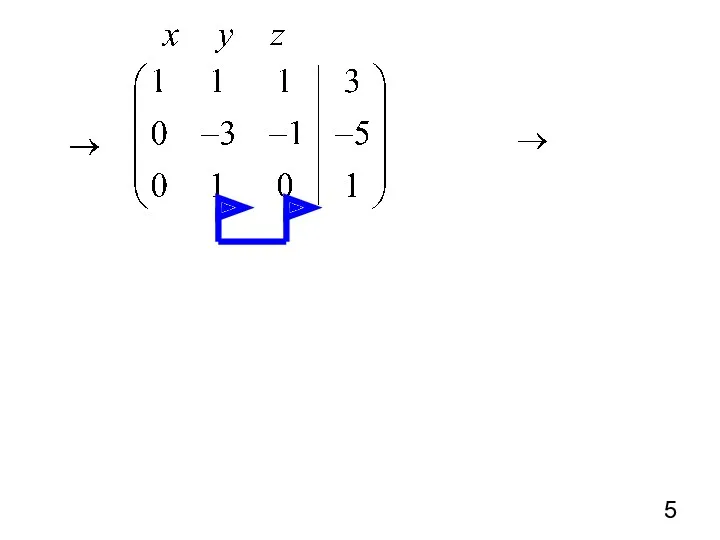



















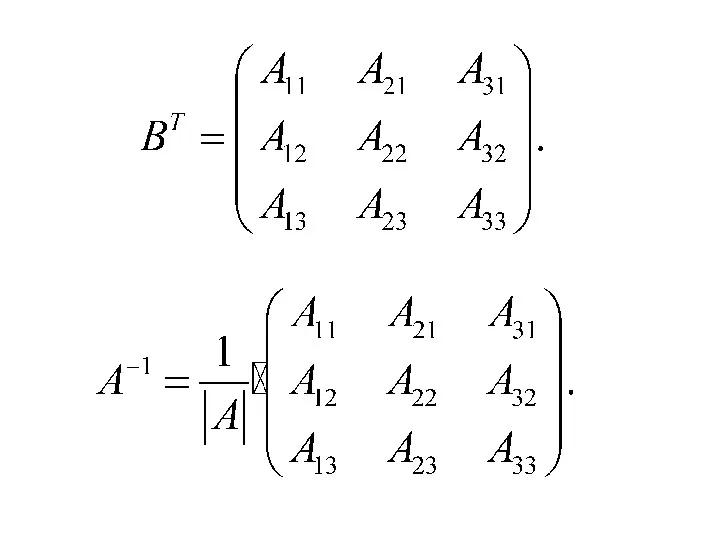



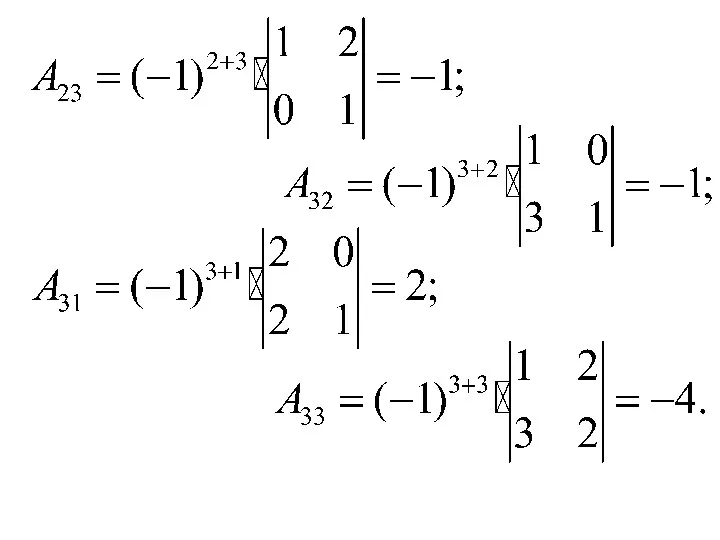
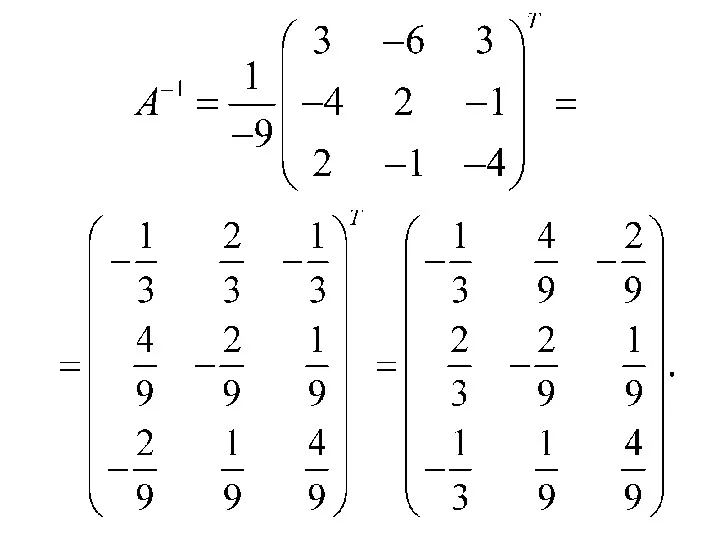

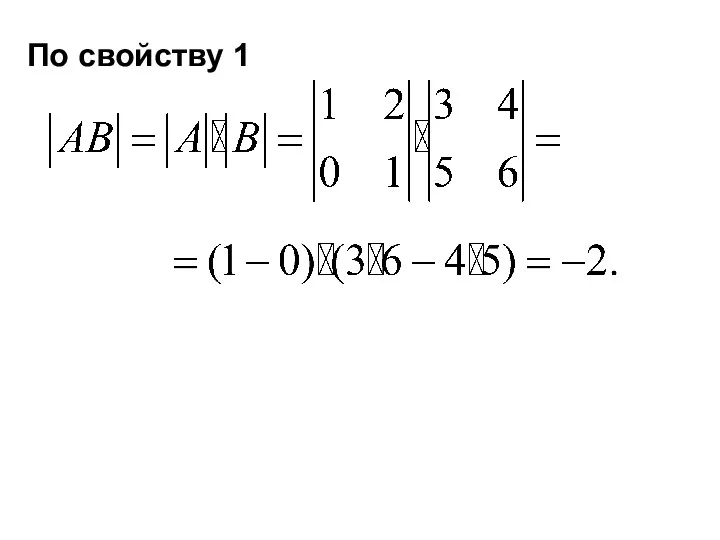

 Числа, кратные 9
Числа, кратные 9 Длина окружности и площадь круга
Длина окружности и площадь круга Додавання раціональних чисел
Додавання раціональних чисел Урок 11. Деление многозначного числа на многозначное с однозначным частным
Урок 11. Деление многозначного числа на многозначное с однозначным частным Математические загадки
Математические загадки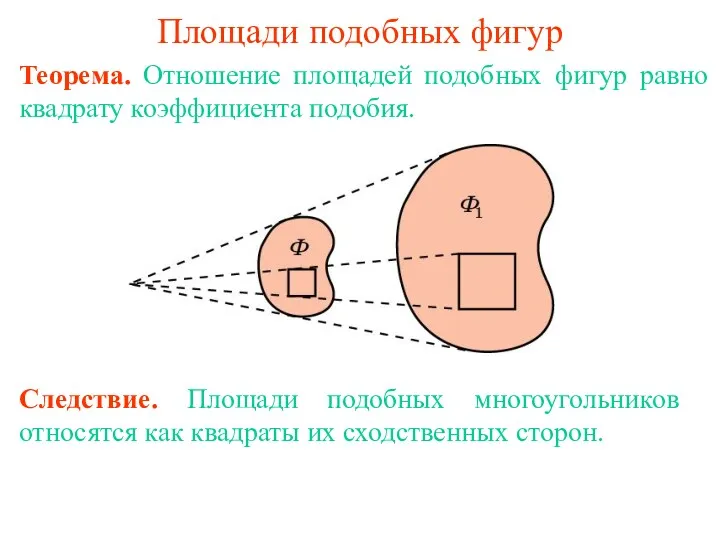 Площади подобных фигур
Площади подобных фигур Графический способ решения систем уравнений
Графический способ решения систем уравнений Урок математики 3 класс УМК Школа 2100на тему Круг. Окружность.
Урок математики 3 класс УМК Школа 2100на тему Круг. Окружность. применение производной к исследованию функции
применение производной к исследованию функции Дисперсия и ее свойства
Дисперсия и ее свойства Иррациональные уравнения
Иррациональные уравнения Геометрические фигуры
Геометрические фигуры Викторина для 5 - 6 классов
Викторина для 5 - 6 классов Единицы длины. Миллиметр. 2 класс
Единицы длины. Миллиметр. 2 класс Комбинаторика. Вероятность
Комбинаторика. Вероятность Квадратні нерівності. Розв’язування квадратних нерівностей
Квадратні нерівності. Розв’язування квадратних нерівностей Задачи на построение треугольника
Задачи на построение треугольника Решение задач: Первый признак подобия треугольников
Решение задач: Первый признак подобия треугольников Творческий проект учащихся 7 класса Симметрия вокруг нас
Творческий проект учащихся 7 класса Симметрия вокруг нас Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Задачи: классификация, методы решения, граничные условия
Задачи: классификация, методы решения, граничные условия Правильные многогранники. Решение задач
Правильные многогранники. Решение задач Решение задач по теме Сложение и вычитание дробей с разными знаменателями
Решение задач по теме Сложение и вычитание дробей с разными знаменателями Метр — одиниця довжини. Наступне і попереднє числа
Метр — одиниця довжини. Наступне і попереднє числа Виды углов и их сравнение. Презентация.
Виды углов и их сравнение. Презентация. Функции и ее графики
Функции и ее графики Умножение. Свойства умножения
Умножение. Свойства умножения Своя игра. (6 класс)
Своя игра. (6 класс)