Содержание
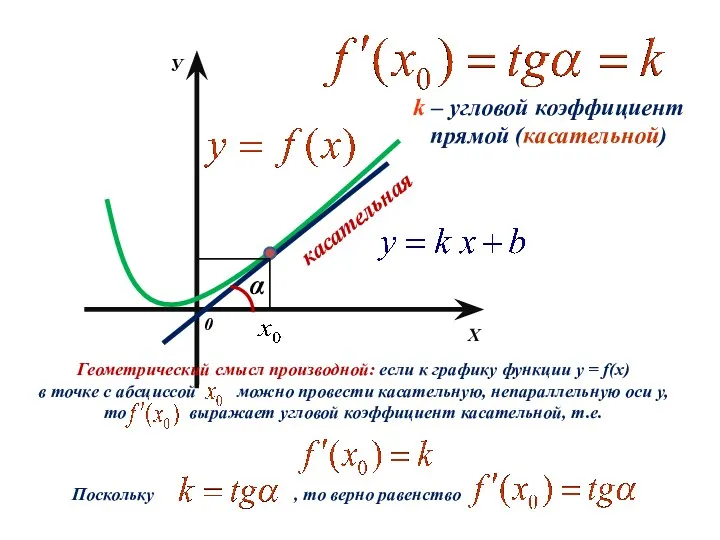
- 2. Х У 0 касательная α k – угловой коэффициент прямой (касательной) Геометрический смысл производной: если к
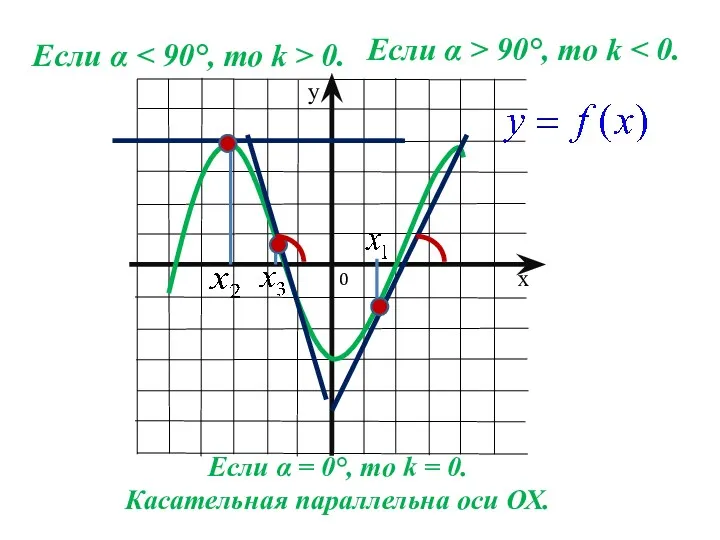
- 3. Если α 0. Если α > 90°, то k Если α = 0°, то k =
- 4. Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f!(х)≥0 (причем равенство f!(х)=0 выполняется
- 5. Пример: Исследовать на монотонность функцию у=2х3+3х2 – 1. Исследовать функцию на монотонность – это значит выяснить,
- 6. f!(х)=6х2+6х=6х (х+1) Если функция непрерывна не только на открытом промежутке, но и в его концевых точках
- 7. Точки экстремума функции и их нахождение Рассмотрим график функции у=2х3+3х2–1 х у - 1 0 На
- 8. Определение 1. Точку х=х0 называют точкой минимума функции у = f(х), если у этой точки существует
- 9. Значение максимума и минимума обозначаются: уmax , ymin соответственно. ВНИМАНИЕ!!! Только не путать с наибольшим (или
- 10. Теорема 4. Если функция у = f(х) имеет экстремум в точке х=х0, то этой точке производная
- 11. Теорема 5 (достаточные условия экстремума). Пусть функция у = f(х) непрерывна на промежутке Х и имеет
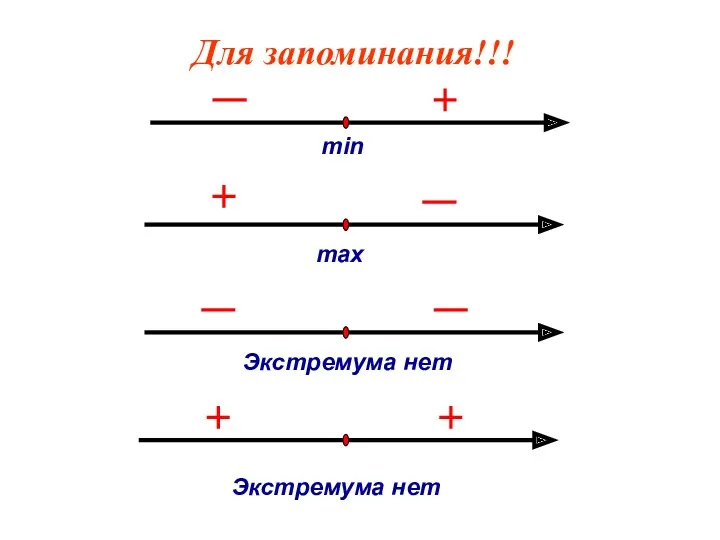
- 12. Для запоминания!!! min max Экстремума нет Экстремума нет
- 13. Пример:Найти точки экстремума функции у=3х4 – 16х3 + 24х2 – 11. Решение: найдем производную данной функции:
- 14. Алгоритм исследования непрерывной функции у=f(х) на монотонность и экстремумы: Найти производную f1(х). Найти стационарные (f1(х)=0) и
- 15. Пример: Исследовать функцию на монотонность и экстремумы
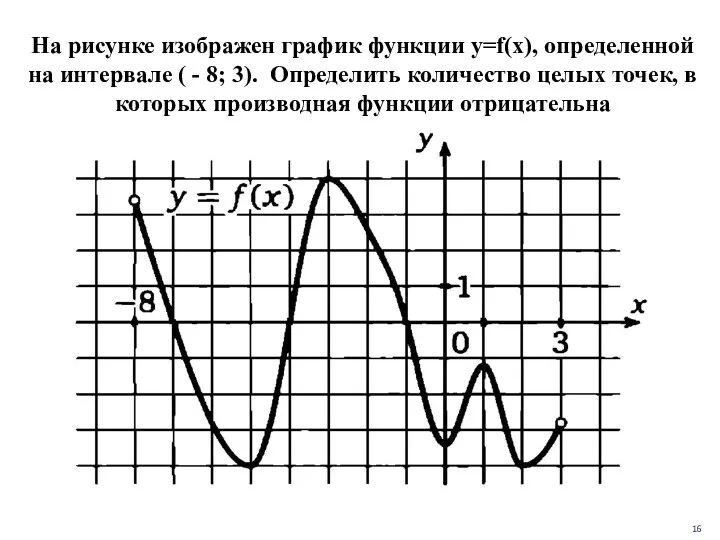
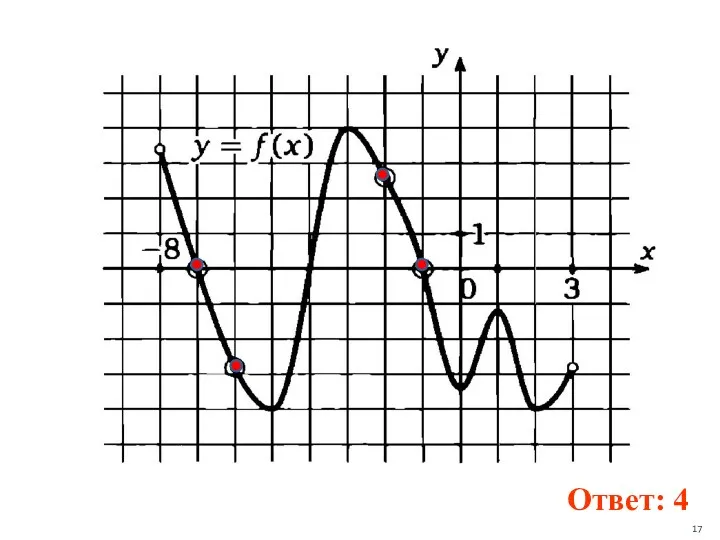
- 16. На рисунке изображен график функции y=f(x), определенной на интервале ( - 8; 3). Определить количество целых
- 17. Ответ: 4
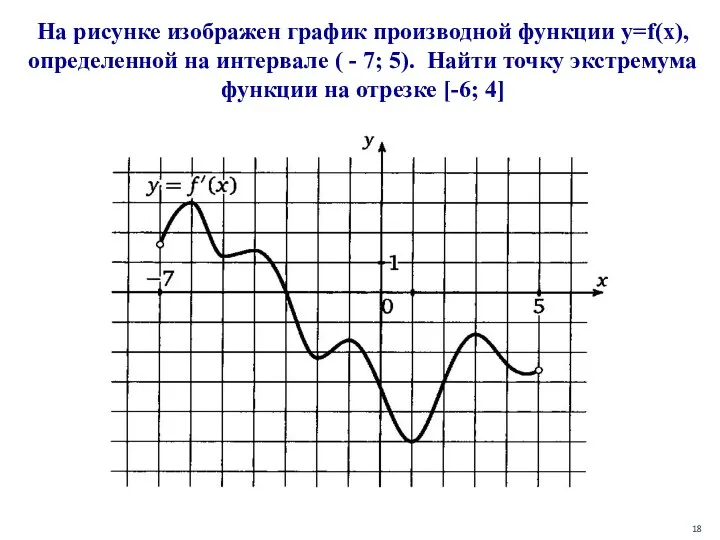
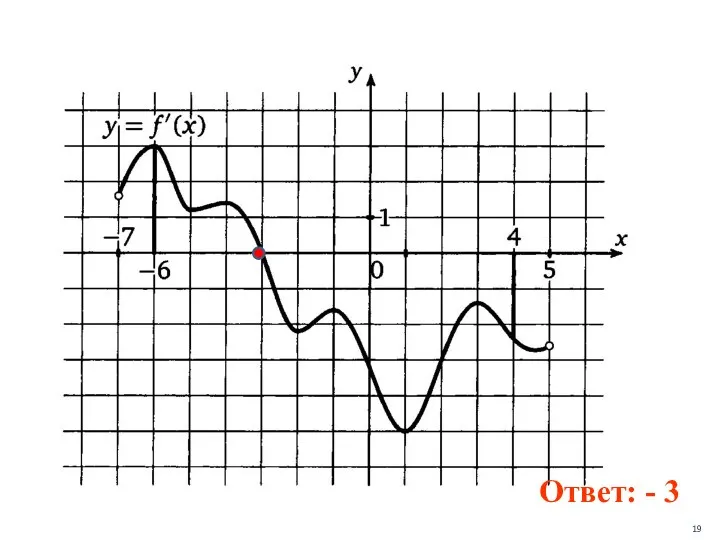
- 18. На рисунке изображен график производной функции y=f(x), определенной на интервале ( - 7; 5). Найти точку
- 19. Ответ: - 3
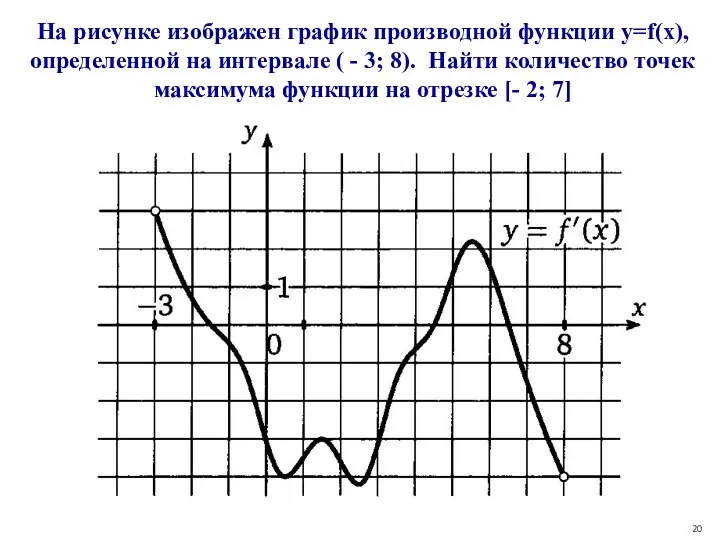
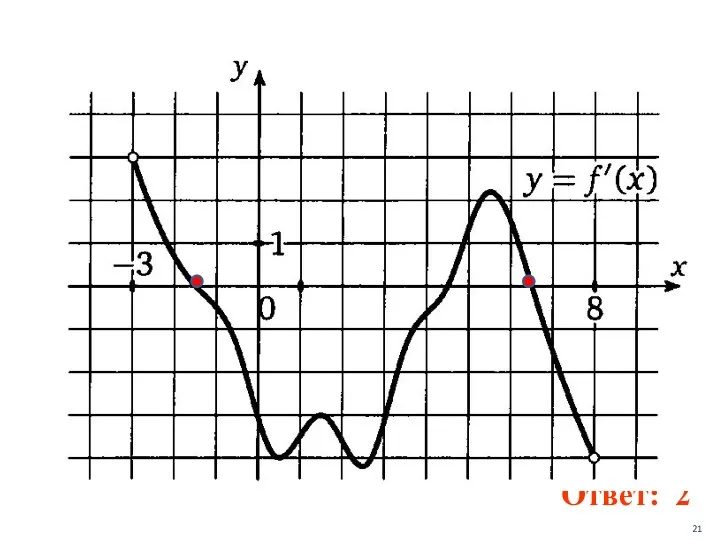
- 20. На рисунке изображен график производной функции y=f(x), определенной на интервале ( - 3; 8). Найти количество
- 21. Ответ: 2
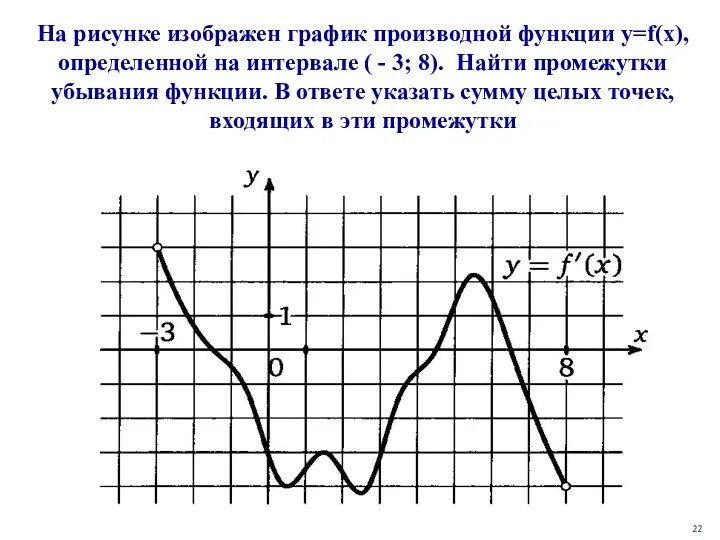
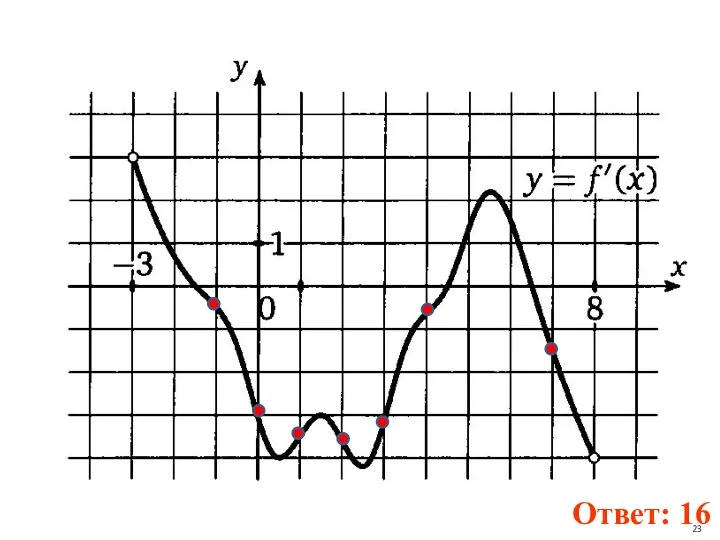
- 22. На рисунке изображен график производной функции y=f(x), определенной на интервале ( - 3; 8). Найти промежутки
- 23. Ответ: 16
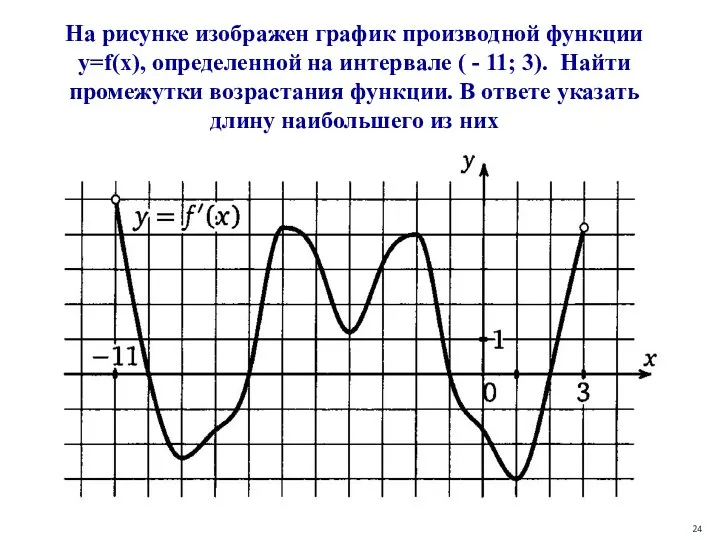
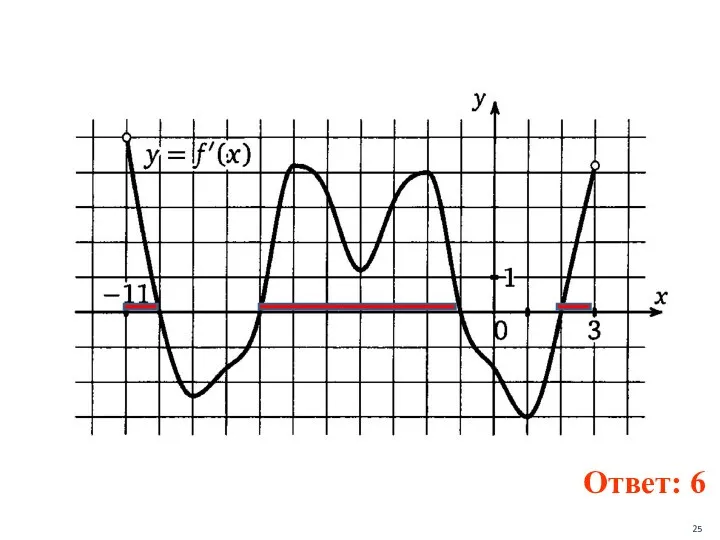
- 24. На рисунке изображен график производной функции y=f(x), определенной на интервале ( - 11; 3). Найти промежутки
- 25. Ответ: 6
- 27. Скачать презентацию











 Занимательная математика 1 класс
Занимательная математика 1 класс Сложение, вычитание и умножение обыкновенных дробей
Сложение, вычитание и умножение обыкновенных дробей Степень с натуральным, целым и рациональным показателем. Свойства степеней
Степень с натуральным, целым и рациональным показателем. Свойства степеней Применение метода интервалов для решения неравенст. 9 класс
Применение метода интервалов для решения неравенст. 9 класс Длина окружности. Площадь круга
Длина окружности. Площадь круга Решение задач на совместную работу
Решение задач на совместную работу Урок 30. Линейная функция у = кх
Урок 30. Линейная функция у = кх Школьные годы чудесные .
Школьные годы чудесные . Внеклассное мероприятие Аукцион математических задач
Внеклассное мероприятие Аукцион математических задач работа с задачей
работа с задачей Презентация (из опыта работы).
Презентация (из опыта работы).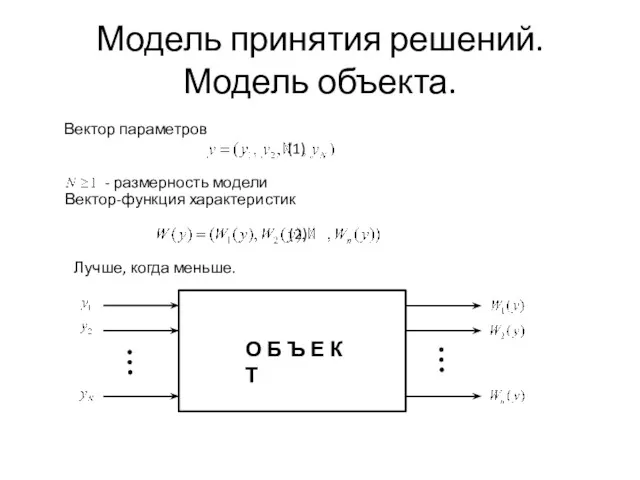 Модель принятия решений. Модель объекта
Модель принятия решений. Модель объекта Поля и линейные пространства
Поля и линейные пространства Свойство медианы равнобедренного треугольника
Свойство медианы равнобедренного треугольника Презентация Развитие элементарных математических представлений с помощью логических блоков Дьенеша у детей дошкольного возраста с ОВЗ
Презентация Развитие элементарных математических представлений с помощью логических блоков Дьенеша у детей дошкольного возраста с ОВЗ Презентация Счет до 5
Презентация Счет до 5 Понятие площади.
Понятие площади. Задачи на построение
Задачи на построение Второй и третий признаки равенства треугольников. Урок 1
Второй и третий признаки равенства треугольников. Урок 1 Основные понятия алгебры логики
Основные понятия алгебры логики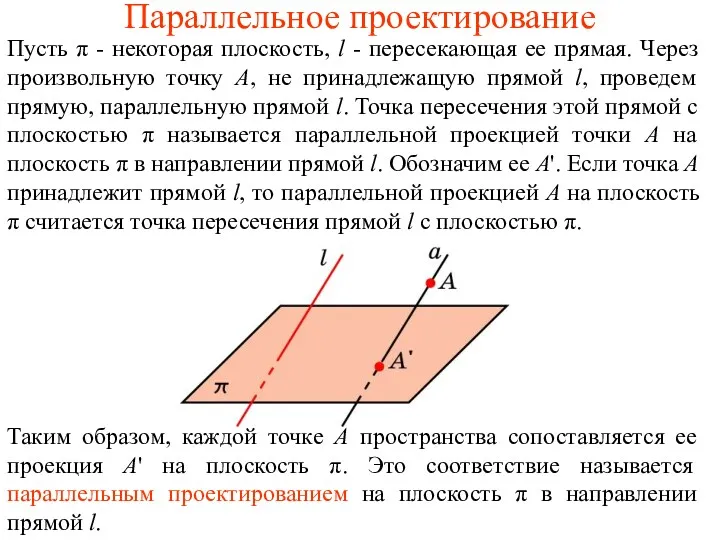 Параллельное проектирование
Параллельное проектирование Избранные главы математики
Избранные главы математики Степени и корни. Степенные функции
Степени и корни. Степенные функции Цилиндр, конус и шар
Цилиндр, конус и шар Нахождение дроби от числа. 6 класс. Для коррекционных классов
Нахождение дроби от числа. 6 класс. Для коррекционных классов Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 8.
Интерактивный тренажёр. В гости к Смешарикам Таблица умножения и деления на 8. Сущность и содержание метрологии. (Лекция 1)
Сущность и содержание метрологии. (Лекция 1) Задания по математике
Задания по математике