Слайд 2

План
3.1 Загальна економіко-математична модель задачі лінійного програмування.
3.2 Форми запису задач
лінійного програмування.
3.3 Геометрична інтерпретація задачі лінійного програмування.
3.4 Основні властивості розв’язків задачі лінійного програмування.
3.5 Графічний метод розв’язування задач лінійного програмування.
Слайд 3

Загальна економіко-математична модель задачі лінійного програмування
(3.1)
(3.2)
(3.3)
Слайд 4

Допустимий розв’язок (план) задачі лінійного програмування
Х = (х1, х2, …,
хn)
Оптимальний розв’язок (план) задачі лінійного програмування
Слайд 5
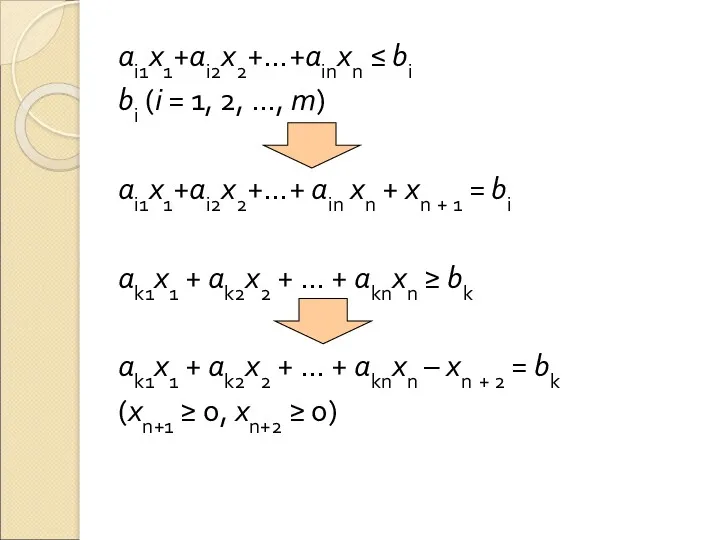
аi1х1+аi2х2+…+аinxn ≤ bi
bi (i = 1, 2, …, m)
ai1x1+ai2x2+…+ ain
xn + xn + 1 = bi
аk1x1 + ak2x2 + … + aknxn ≥ bk
ak1x1 + ak2x2 + … + aknxn – xn + 2 = bk
(хn+1 ≥ 0, хn+2 ≥ 0)
Слайд 6

Форми запису задач лінійного програмування
(3.4)
Слайд 7
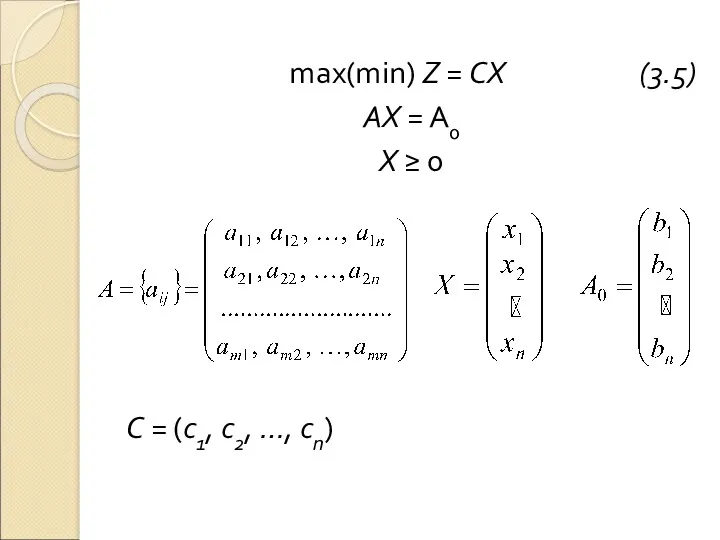
max(min) Z = CX (3.5)
АХ = А0
Х ≥ 0
С
= (с1, с2, …, сп)
Слайд 8
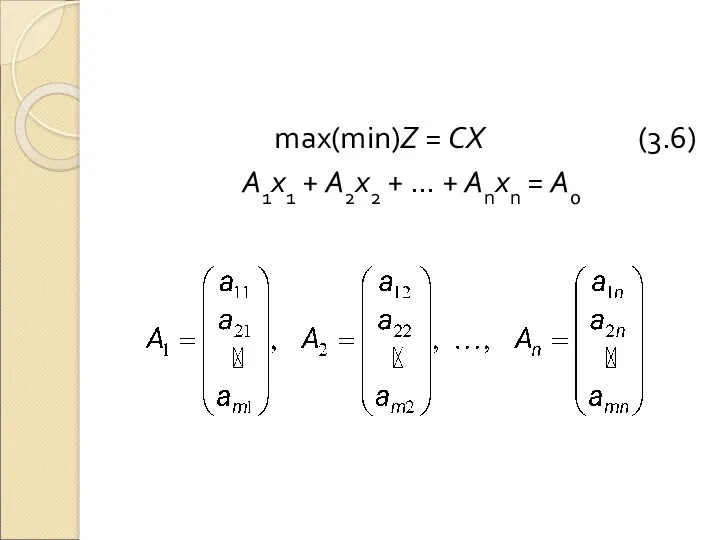
max(min)Z = CX (3.6)
A1x1 + A2x2 + … + Anxn =
A0
Слайд 9

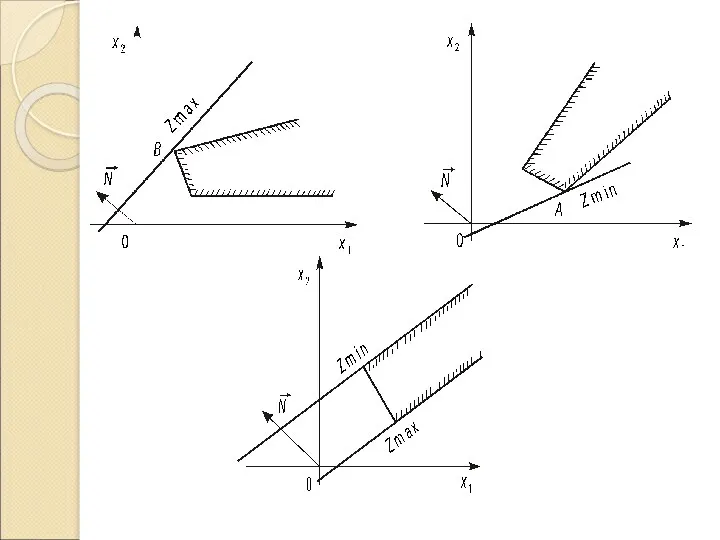
Геометрична інтерпретація задачі лінійного програмування
х1Оx2
(3.7)
ai1x1 + ai2x2 =
bi (i=1,2, ..., т)
Слайд 10
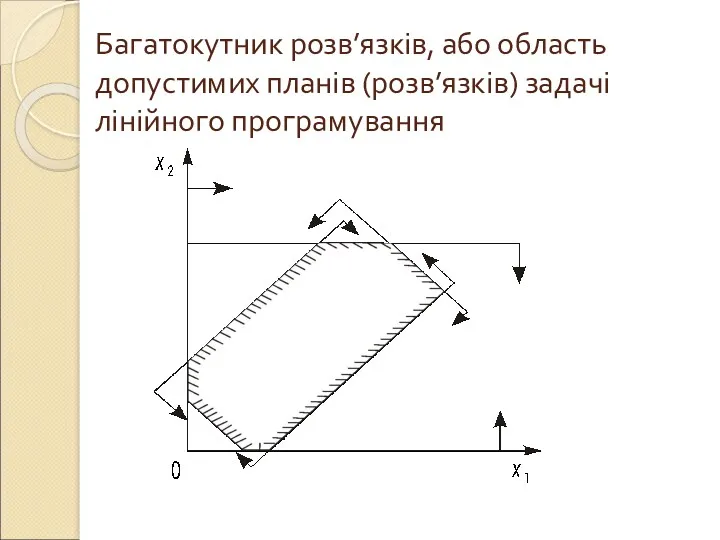
Багатокутник розв’язків, або область допустимих планів (розв’язків) задачі лінійного програмування
Слайд 11
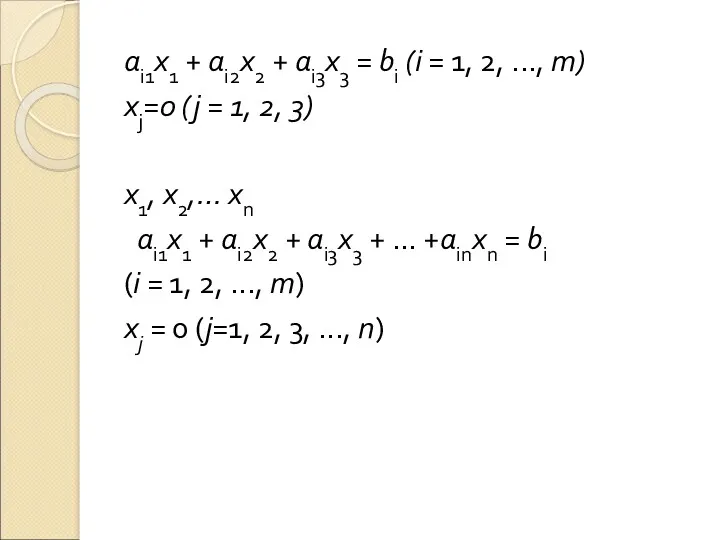
ai1x1 + ai2x2 + ai3x3 = bi (i = 1, 2,
..., т)
хj=0 (j = 1, 2, 3)
х1, х2,… хn
аi1x1 + ai2x2 + ai3x3 + … +ainxn = bi
(i = 1, 2, ..., т)
хj = 0 (j=1, 2, 3, ..., n)
Слайд 12
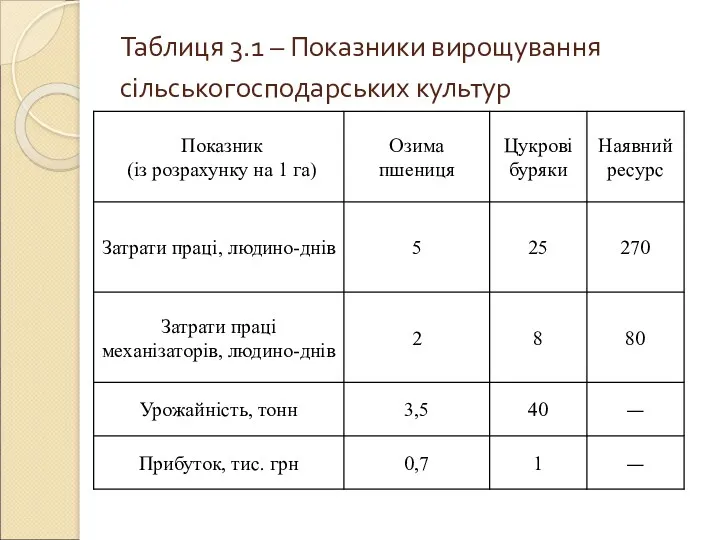
Таблиця 3.1 – Показники вирощування сільськогосподарських культур
Слайд 13

Задача лінійного програмування має такий вигляд:
max Z = 0,7x1 + x2
(3.8)
за умов:
x1 + x2 ≤ 20; (3.9)
5x1 + 25x2 ≤ 270; (3.10)
2x1 + 8x2 ≤ 80; (3.11)
x2 ≥ 5; (3.12)
x1 ≥ 0, x2 ≥ 0. (3.13)
Слайд 14
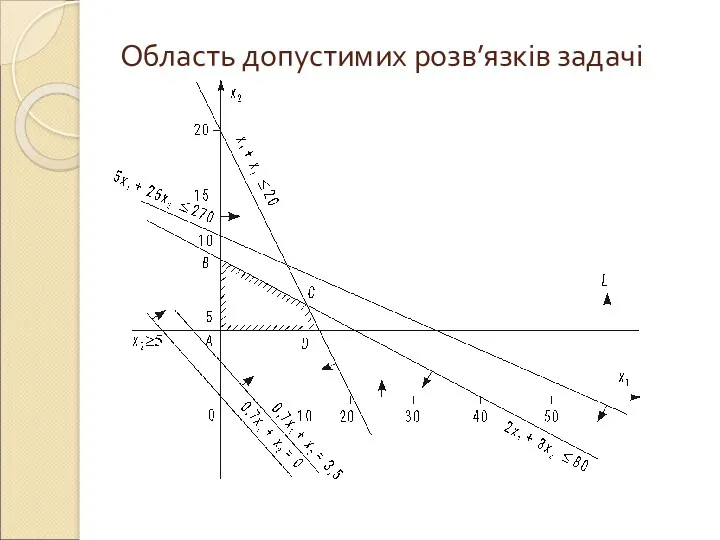
Область допустимих розв’язків задачі
Слайд 15

Основні властивості розв’язків задачі лінійного програмування
Властивість 1. (Теорема 3.1) Множина
всіх планів задачі лінійного програмування опукла.
Властивість 2. (Теорема 3.2) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
Слайд 16

Властивість 3. (Теорема 3.3) Якщо відомо, що система векторів A1, A2,
…, Ak (k≤n) у розкладі A1x1 +A2x2 + … + Anxn = A0, X≥0 лінійно незалежна і така, що
A1x1 + A2x2 + … + Akxk = A0,
де всі xj ≥ 0, то точка X = (x1, x2, …, xk, 0, …, 0) є кутовою точкою багатогранника розв’язків.
Властивість 4. (Теорема 3.4) Якщо X = (x1, x2, …, xn) – кутова точка багатогранника розв’язків, то вектори в розкладі
A1x1 + A2x2 + … + Anxn = A0, X ≥ 0,
що відповідають додатним xj, є лінійно незалежними.
Слайд 17

Графічний метод розв’язування задач лінійного програмування
(3.15)
(3.16)
(3.17)
(і
= 1, 2, …, т)
Слайд 18

Алгоритм графічного методу
1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях
задачі (3.16) знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
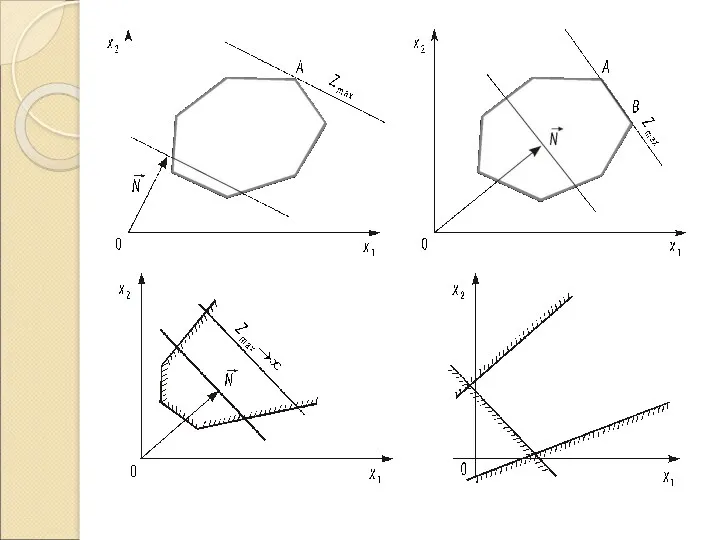
4. Будуємо вектор , що задає напрям зростання значення цільової функції задачі.
Слайд 19

5. Будуємо пряму с1х1+с2х2=const, перпендикулярну до вектора .
6. Рухаючи пряму с1х1+с2х2=const
в напрямку вектора (для задачі максимізації) або в протилежному напрямі
(для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення.
7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
Слайд 20
Слайд 21
Слайд 22
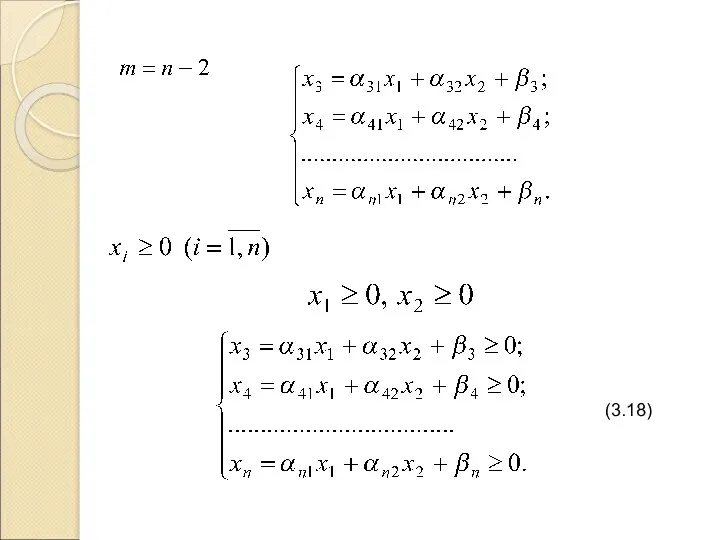



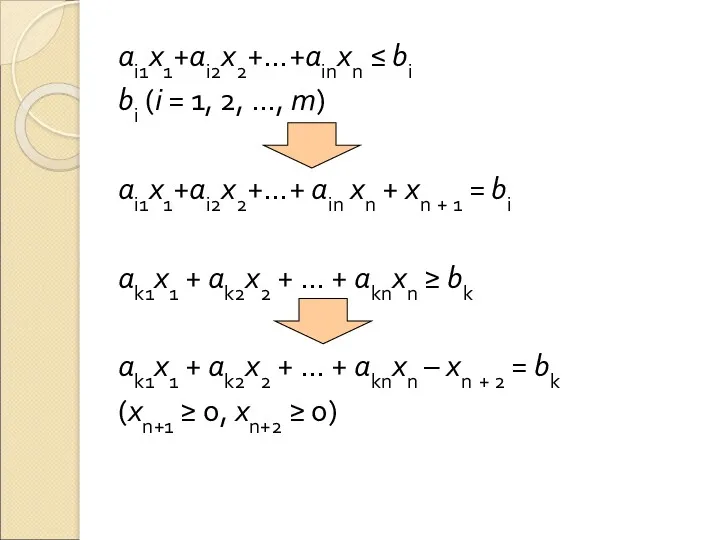


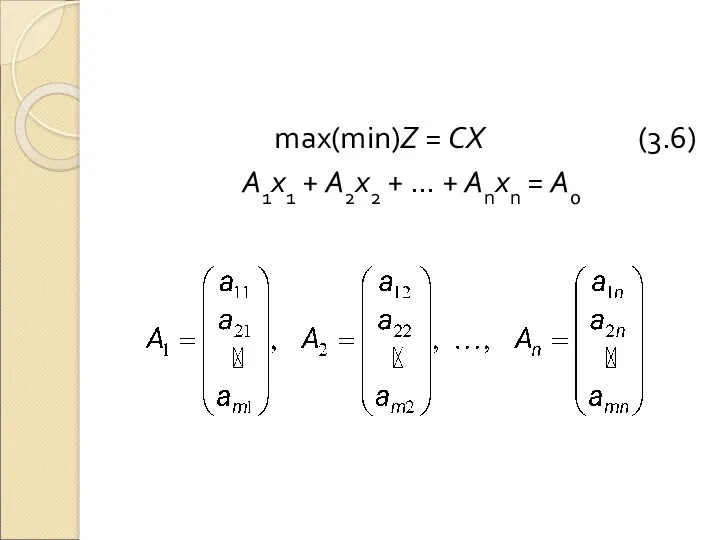


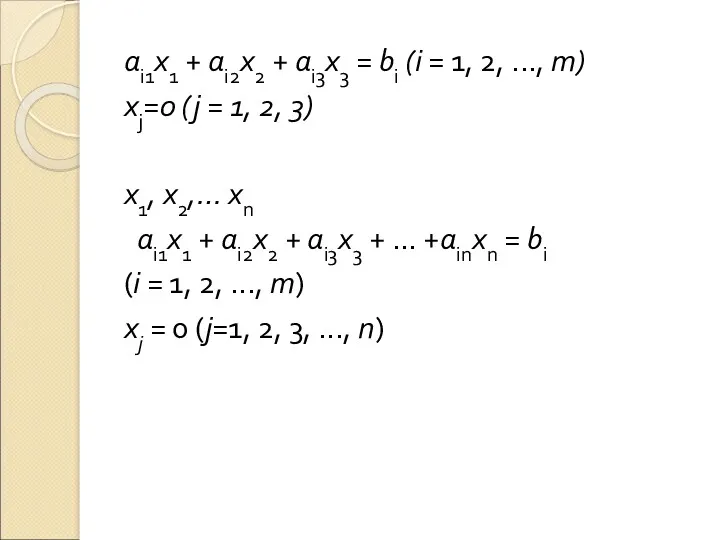










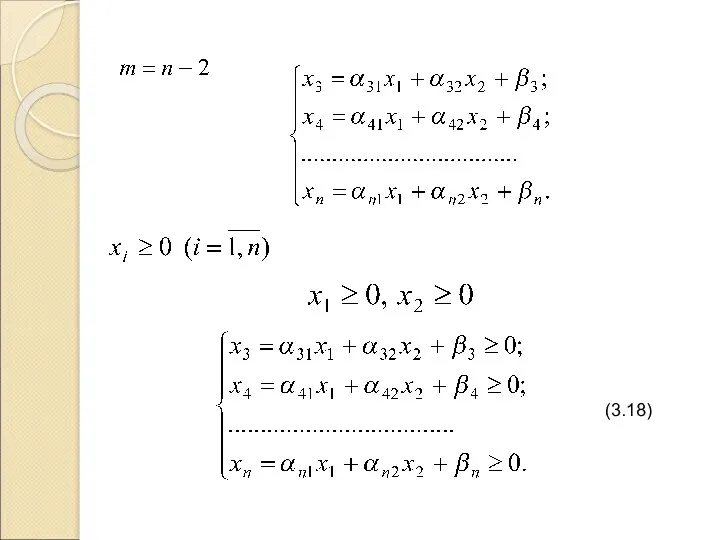
 Распределительное свойство умножения
Распределительное свойство умножения Метод крутого восхождения
Метод крутого восхождения Сфера. Шар. Части сферы и шара
Сфера. Шар. Части сферы и шара Задачи на готовых чертежах
Задачи на готовых чертежах Формулы для вычисления площадей различных треугольников
Формулы для вычисления площадей различных треугольников Множества. Отношения между множествами
Множества. Отношения между множествами Сложение чисел с разными знаками
Сложение чисел с разными знаками Особенности урока математики в начальной школе в соответствии с ФГОС ΙΙ поколения.
Особенности урока математики в начальной школе в соответствии с ФГОС ΙΙ поколения. Угол между прямыми в пространстве
Угол между прямыми в пространстве Математические модели в экономике
Математические модели в экономике Қарапайым математикалық түсініктер. Уақытты бағдарлау
Қарапайым математикалық түсініктер. Уақытты бағдарлау Задачи на движение в разных направлениях (схемы)
Задачи на движение в разных направлениях (схемы) урок математики в 1 классе
урок математики в 1 классе Системы линейных уравнений. Ранг матрицы
Системы линейных уравнений. Ранг матрицы Магія чисел. Перевірка домашнього завдання
Магія чисел. Перевірка домашнього завдання Угол. Прямой и развернутый угол. 5 класс
Угол. Прямой и развернутый угол. 5 класс Трапеция. 8 класс
Трапеция. 8 класс Интерактивная игра Цвет и форма
Интерактивная игра Цвет и форма Тренажер по математике №2. Сложение и вычитание в пределах 10
Тренажер по математике №2. Сложение и вычитание в пределах 10 Метод координат в решении задач С2
Метод координат в решении задач С2 Симметрия относительно плоскости
Симметрия относительно плоскости Решение уравнений
Решение уравнений Квадратные уравнения. Решение уравнений
Квадратные уравнения. Решение уравнений Как писать цифры
Как писать цифры Поворот точки вокруг начала координат
Поворот точки вокруг начала координат Использование на уроках математики программы Geogebra и платформы Гуглкласс
Использование на уроках математики программы Geogebra и платформы Гуглкласс Устный счет для 1 класса
Устный счет для 1 класса Дидактическая электронная игра
Дидактическая электронная игра