Системы линейных уравнений. Ранг матрицы презентация

Система m линейных уравнений с n переменными имеет вид:
- коэффициенты системы,
- свободные члены.
Решением системы называется такая совокупность значений, при подстановке которых каждое уравнение системы обращается в верное равенство.

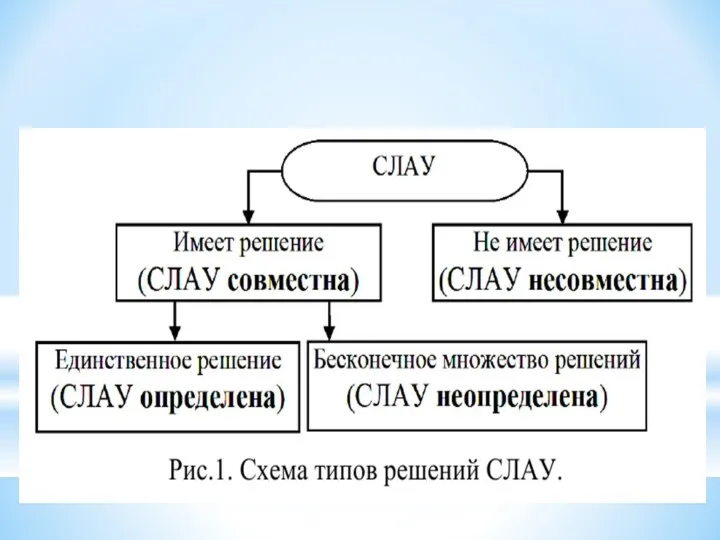
совместной, если она имеет хотя бы одно решение;
несовместной, если она не имеет решений;
определенной, если она имеет единственное решение;
неопределенной, если она имеет более одного решения;
однородной, если все bi=0;
неоднородной, если не все bi=0.
Система линейных уравнений называется:

Исследование систем линейных уравнений
Теорема Кронекера - Капелли. Для того, чтобы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, чтобы ранг расширенной матрицы системы равнялся рангу матрицы коэффициентов:

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы
Ранг матрицы А обозначается rang A
или r(A).
Алгоритм нахождения ранга способом перебора миноров:
1.При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).

2.Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум. И так далее, по аналогии.

Матрица А имеет 4 минора 3 - его порядка, например:
18 миноров 2 - го порядка, например:
12 миноров 1 - го порядка – сами элементы.
Наибольший порядок отличного от нуля минора этой матрицы равен 3, поэтому:

Ранг матрицы можно найти:
• по определению
• методом окаймляющих миноров
• методом Гаусса (с помощью элементарных преобразований)
Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то r(A) =r(B).

Теорема.
Эквивалентные (элементарные) преобразования не меняют ранга матриц
Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.

Умножение или деление элементов одного ряда на одно и то же число, не равное нулю
Перестановка местами двух рядов
Прибавление к элементам ряда элементов другого параллельного ряда, умноженного на произвольный множитель
Эквивалентные преобразования:
Вычеркивание нулевого ряда

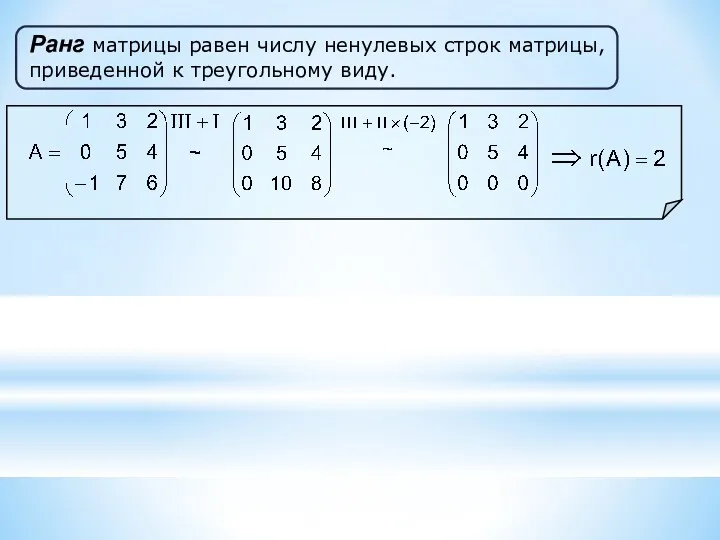
Ранг матрицы равен числу ненулевых строк матрицы, приведенной к треугольному виду.

Алгоритм исследования СЛАУ
1.Записываем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
2. Используя понятие ранга матрицы и теоремы Кронекера-Капелли определяем вид системы.

Система имеет r базисных переменных и n – r свободных переменных.
Общее решение системы запишется в виде:
Бесконечное множество решений:

Решение
совместна
2 базисных переменных, т.к.
неопределенна
1 свободная переменная, т.к.
Восстановим систему:
например,
например,
Пример. Решить систему:

Однородные системы линейных уравнений
Однородная система всегда имеет решение:
- тривиальное решение.