Содержание
- 2. ПЛАН
- 3. ПОНЯТТЯ ВЕКТОРА
- 4. ПОНЯТТЯ ВЕКТОРА Г. Грассман В. Гамільтон
- 5. ЗАСТОСУВАННЯ ВЕКТОРА
- 6. МАТЕМАТИЧНЕ ПОНЯТТЯ ВЕКТОРА
- 7. ВЕКТОР. ПОЗНАЧЕННЯ ВЕКТОРА Вектором називається напрямлений відрізок, тобто відрізок в якому виділено початок і кінець Вектори
- 8. МОДУЛЬ ВЕКТОРА Абсолютною величиною (або модулем) називається довжина відрізка, що задає вектор. Абсолютна величина нуль-вектора дорівнює
- 9. НАПРЯМ ВЕКТОРА Вектори АВ і CD називаються однаково напрямленими, якщо однаково напрямлені і півпрямі АВ і
- 10. РІВНІСТЬ ВЕКТОРІВ
- 11. КООРДИНАТИ ВЕКТОРА Координатами вектора а з початком А(х1 ; у1 ) і кінцем В(х2 ; у2
- 12. ЗАДАЧА №1 Дано точки А(3;5) і В(-3;3). Знайдіть координати вектора АВ. Дано вектор а(3;4). Знайти абсолютну
- 13. РОЗВ’ЯЗАННЯ №1 АВ(-3-3;3-5) =АВ(-6;-2). Відповідь. АВ(-6;-2) ІаІ = = = Відповідь. ІаІ= 5. РОЗВ’ЯЗАННЯ №2
- 14. ДІЇ З ВЕКТОРАМИ Сумою векторів а і b з координатами а1, а2 і b1, b2 називається
- 15. ЗАДАЧА №3 Знайдіть координати вектора с, що є сумою векторів а(4;8) і b(-4;5). Нехай с(c1; с2
- 16. ДОДАВАННЯ ВЕКТОРІВ А В С А В С D
- 17. ВІДНІМАННЯ ВЕКТОРІВ А В С a a-b b
- 18. ЗАДАЧА №4 ЗАДАЧА№5 Дано вектори а і b (див.рис.). Побудувати вектор: с = а + b.
- 19. ПОБУДОВА №4 ПОБУДОВА №5 а b b c a b a- b
- 20. МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО. Добутком вектора (а1;а2) на число λ називається вектор (λа1; λа2), тобто (а1;а2)
- 21. ЗАДАЧА №6 ЗАДАЧА №7 Дано вектори с (-3 ; 8 ) і b (4; 16). Обчислити
- 22. РОЗВ’ЯЗАННЯ №6 ПОБУДОВА №7 1.Знайдемо координати вектора b b = ( 4; 16 ) = =(
- 23. КОЛІНЕАРНІ ВЕКТОРИ Два ненульових вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних
- 24. Якщо вектори колінеарні, то їх відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні,
- 25. ЗАДАЧА № 8 Дано чотири точки А(3;0), В(0;1), С(2;7) і D(5;6). Доведіть, що вектори АВ і
- 26. ДОВЕДЕННЯ 1.Знайдемо координати вектора АВ. АВ (0-3;1-0) =АВ(-3; 1); 2.Знайдемо координати вектора СD. СD (5 –
- 27. РОЗКЛАДАННЯ ВЕКТОРА ЗА ДВОМА НЕКОЛІНЕАРНИМИ ВЕКТОРАМИ с = λа + μb Будь – який вектор с
- 28. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ Скалярним добутком векторів а(а1;а2) і b(b1;b2) називається число а1b1+a2b2 Якщо а ∙ b
- 29. ЗАДАЧА № 9 ЗАДАЧА № 10 Знайти кут між векторами а і b, якщо І а
- 31. Скачать презентацию
 Точка рівновіддалена від сторін многокутника
Точка рівновіддалена від сторін многокутника Решение задач на готовых чертежах. Подобные
Решение задач на готовых чертежах. Подобные Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс
Сложение и вычитание многозначных чисел. Закрепление. Деловая игра. 4 класс Деление суммы на число
Деление суммы на число Делим числа урок 46
Делим числа урок 46 Параллельные прямые
Параллельные прямые Видатні математики
Видатні математики Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Мультимедийная разработка урока по алгебре. 10 класс
Мультимедийная разработка урока по алгебре. 10 класс Оптимізаційні економіко- математичні моделі (Лекція 2)
Оптимізаційні економіко- математичні моделі (Лекція 2)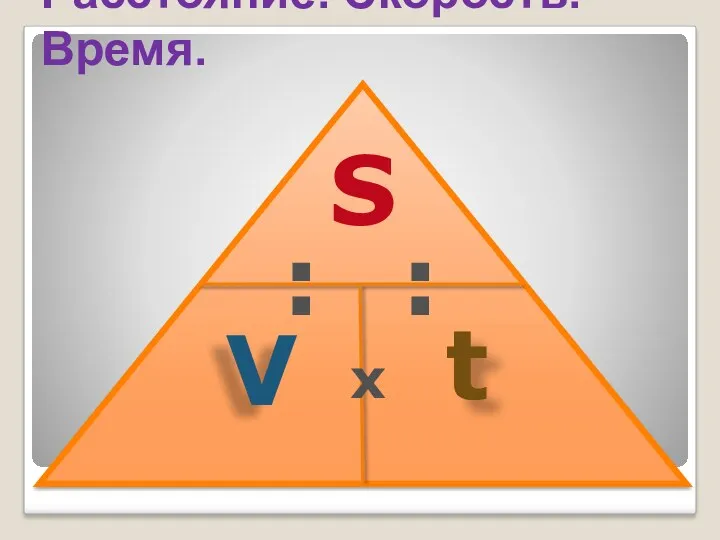 треугольники-помощники
треугольники-помощники Информационно-исследовательский проект Магический куб
Информационно-исследовательский проект Магический куб Стандартный вид числа
Стандартный вид числа Наглядная геометрия, 2 класс.
Наглядная геометрия, 2 класс. Радианная мера угла
Радианная мера угла Формулы квадрата суммы и квадрата разности двух выражений
Формулы квадрата суммы и квадрата разности двух выражений Размерности. Подобие. Моделирование
Размерности. Подобие. Моделирование Законы распределения случайных величин. (Лекция 5)
Законы распределения случайных величин. (Лекция 5) Теорема Пифагора. Решение задач. 8 класс
Теорема Пифагора. Решение задач. 8 класс Четырехугольники. Свойства четырехугольников
Четырехугольники. Свойства четырехугольников Презентация к уроку математики в 1 классе.
Презентация к уроку математики в 1 классе. Треугольник
Треугольник Презентация к уроку математики . 2 класс.
Презентация к уроку математики . 2 класс. Решай! Смекай! Отгадывай! Математическая игра
Решай! Смекай! Отгадывай! Математическая игра математика, 1 класс
математика, 1 класс Натуральные числа. Подготовка к контрольной работе
Натуральные числа. Подготовка к контрольной работе Предмет и методы математической статистики. Понятие и свойства статистической совокупности и выборки
Предмет и методы математической статистики. Понятие и свойства статистической совокупности и выборки Предел последовательности
Предел последовательности