Содержание
- 2. Задача о вычислении мгновенной скорости s ( t ) = 4 t ² Вычислим v ср
- 3. Общий случай: точка движется по прямой по закону s(t) = f (t) Тогда её мгновенной скоростью
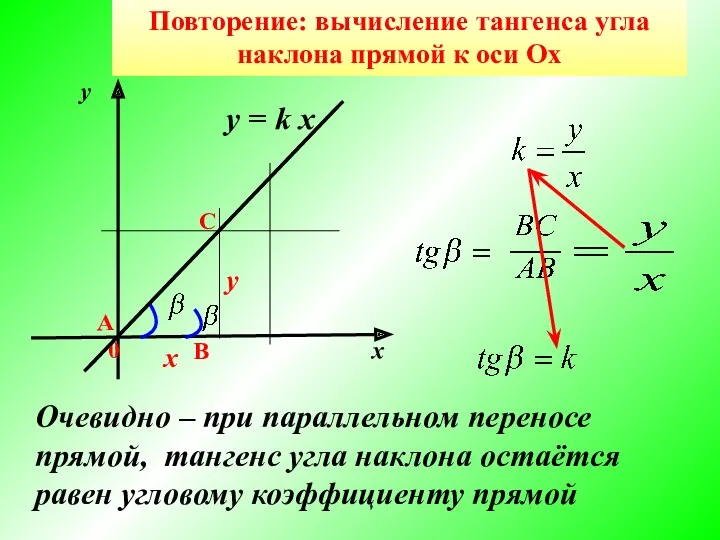
- 4. В у х 0 Повторение: вычисление тангенса угла наклона прямой к оси Ох А С y
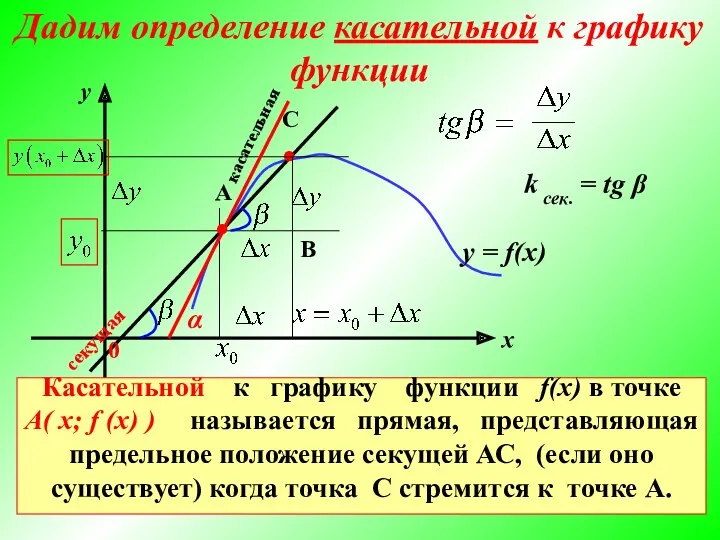
- 5. у = f(x) С ● В касательная Касательной к графику функции f(x) в точке А( х;
- 6. Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей. Секущая Задача о вычислении
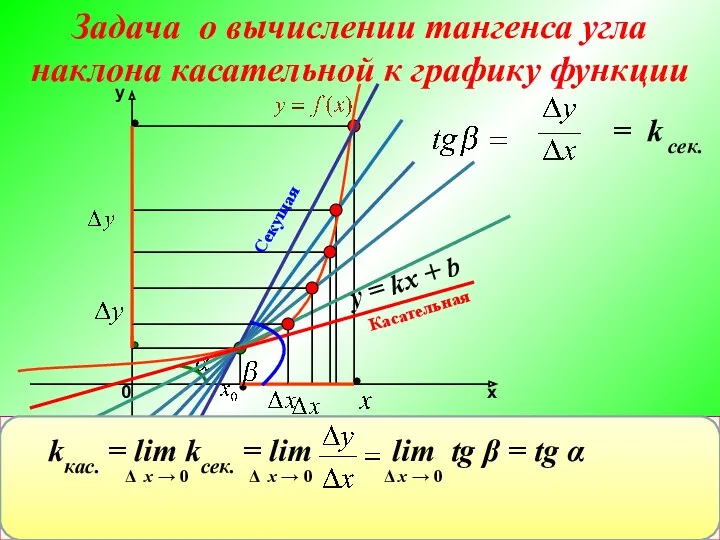
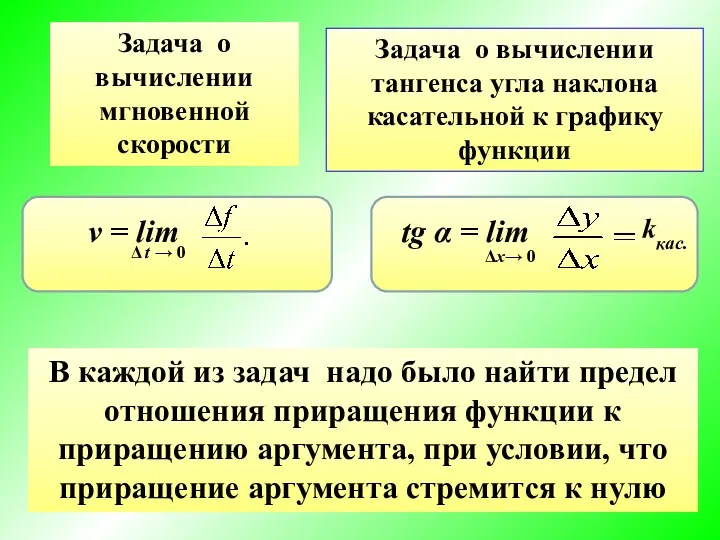
- 7. Задача о вычислении мгновенной скорости Задача о вычислении тангенса угла наклона касательной к графику функции kкас.
- 8. Определение производной
- 9. Историческая справка
- 10. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение,
- 11. В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические
- 12. Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем,
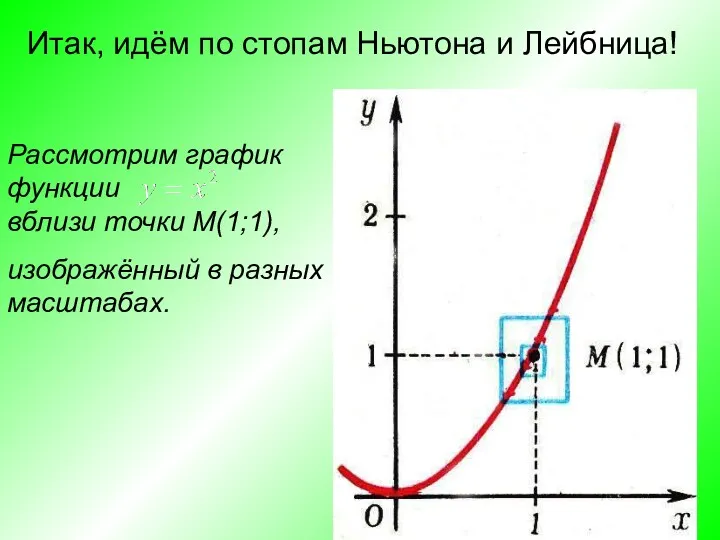
- 13. Итак, идём по стопам Ньютона и Лейбница! Рассмотрим график функции вблизи точки М(1;1), изображённый в разных
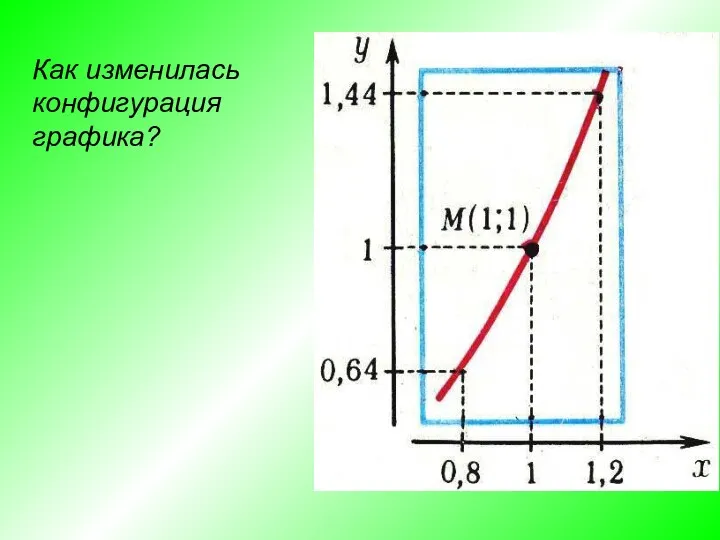
- 14. Как изменилась конфигурация графика?
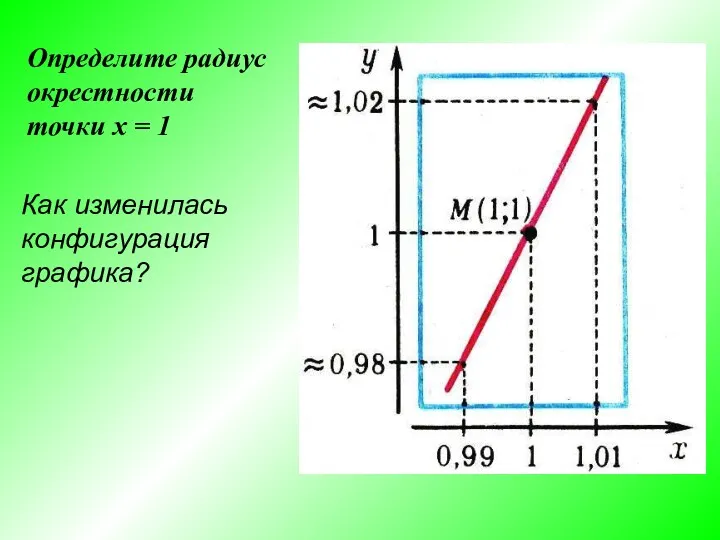
- 15. Определите радиус окрестности точки х = 1 Как изменилась конфигурация графика?
- 16. Основные выводы 1. Чем крупнее масштаб, тем меньше график функции будет отличаться от некоторой прямой, проходящей
- 17. Пусть точка движется вдоль прямой по закону S(t). Тогда за промежуток времени t точка проходит расстояние
- 18. Очевидно, если ∆t 0, то Vср. Vмгн. Значит,
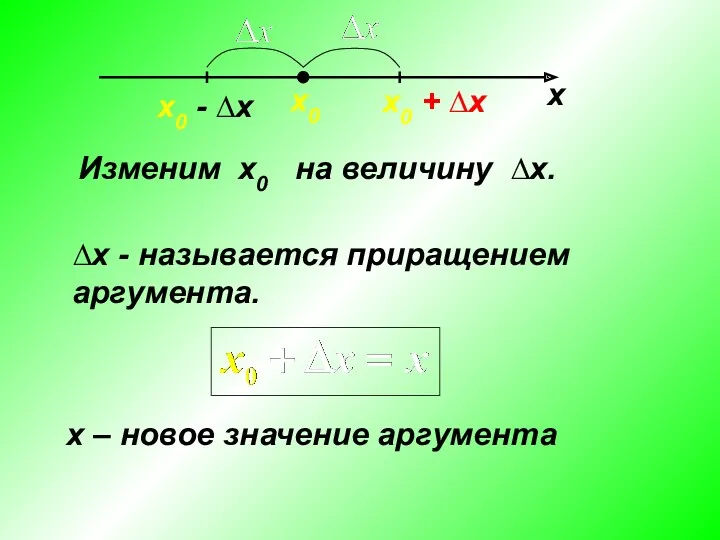
- 19. х х0 Изменим x0 на величину ∆x. ∆x - называется приращением аргумента. x0 + ∆x x0
- 20. Величина y(x) – y(x0) называется приращением функции в точке x0 и обозначается ∆y(x0) .
- 21. Таким образом, чтобы вычислить приращение функции f(x) при переходе от точки x0 к точке x =
- 22. В математике операция нахождения предела отношения приращения функции Δ f к приращению аргумента Δ x ,
- 23. Определение производной
- 24. Определение производной
- 25. Чтобы найти производную функции в точке, надо: найти приращение функции в точке Х0 ; найти отношение
- 26. Пример нахождения производной Решение
- 27. Механический смысл производной Механический смысл производной состоит в том, что производная пути по времени равна мгновенной
- 29. Скачать презентацию


















 Задачи на построение с помощью циркуля и линейки
Задачи на построение с помощью циркуля и линейки Решение прикладных задач с использованием основных свойств вероятности
Решение прикладных задач с использованием основных свойств вероятности Обучение детей решению арифметических задач
Обучение детей решению арифметических задач Прямая и плоскость. Лекция 5
Прямая и плоскость. Лекция 5 Фракталы в природе
Фракталы в природе Число 10
Число 10 Активизация учебно-познавательной деятельности на урока математики на основе внедрения технологии дифференцированного обучения.
Активизация учебно-познавательной деятельности на урока математики на основе внедрения технологии дифференцированного обучения. Углы и отрезки, связанные с окружностью (повторение). 10 класс
Углы и отрезки, связанные с окружностью (повторение). 10 класс Многогранники и тела вращения
Многогранники и тела вращения Первый признак равенства треугольников. Геометрия. 7 класс
Первый признак равенства треугольников. Геометрия. 7 класс Позиционные системы счисления отличные от десятичной
Позиционные системы счисления отличные от десятичной Сложение однозначных чисел с переходом через десяток, вида +2, +3
Сложение однозначных чисел с переходом через десяток, вида +2, +3 Итоговый тест по математике 2 класс
Итоговый тест по математике 2 класс Математика 1 класс УМК Гармония Самостоятельная работа
Математика 1 класс УМК Гармония Самостоятельная работа Математика. Поточная практика 7.1. Аналитическая геометрия. Прямая на плоскости
Математика. Поточная практика 7.1. Аналитическая геометрия. Прямая на плоскости Презентация Секреты таблицы умножения
Презентация Секреты таблицы умножения Приближенные методы решения систем линейных алгебраических уравнений
Приближенные методы решения систем линейных алгебраических уравнений Числа. Целые и рациональные числа. Действительные числа
Числа. Целые и рациональные числа. Действительные числа Предел функции
Предел функции История возникновения и развития геометрии
История возникновения и развития геометрии Математический базар (для учащихся 1-4 классов)
Математический базар (для учащихся 1-4 классов) Методическая разработка урока математики с интерактивным тестом и презентацией. 2 класс.
Методическая разработка урока математики с интерактивным тестом и презентацией. 2 класс. 20231018_otkrytyy_urok_szhatyy
20231018_otkrytyy_urok_szhatyy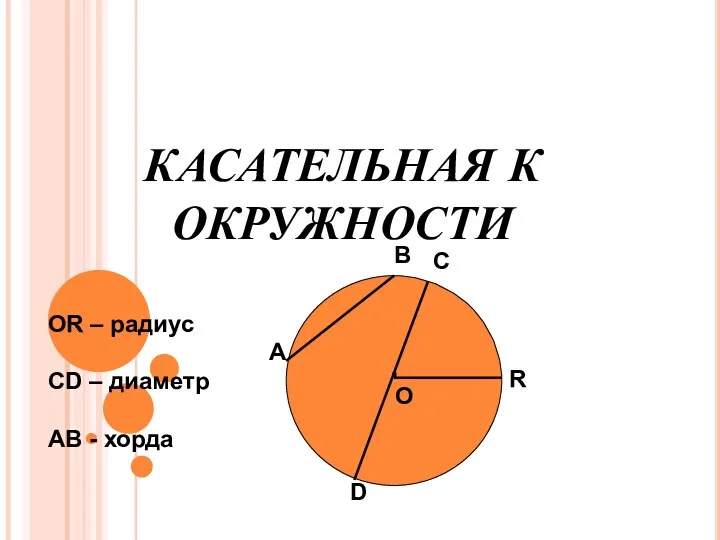 Касательная к окружности
Касательная к окружности Решение задач с величинами цена, количество, стоимость
Решение задач с величинами цена, количество, стоимость Виды многогранников. Связь геометрии и природы
Виды многогранников. Связь геометрии и природы Решение систем уравнений второй степени
Решение систем уравнений второй степени Кому нужна математика
Кому нужна математика