Слайд 2

Слайд 3

ПОНЯТИЕ ЧИСЛОВОЙ ФУНКЦИИ
Переменная х называется аргументом функции или независимой переменной, а
у — значением функции или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости.
Множество X называется областью определения функции f и обозначается D(f). Множество всех у называется множеством значений функции f и обозначается E(f)
Если переменные x и y рассматривать, как декартовы координаты, то графиком функции у = f(x) называется множество точек координатной плоскости ОXY с координатами (x,y).
Слайд 4

Слайд 5

СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
Табличный способ: функция задается таблицей ряда значений аргумента и
соответствующих значений функции.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
Графический способ: задается график функции. Преимуществом графического задания является его наглядность, недостатком — его неточность
Слайд 6

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

СВОЙСТВА ОБРАТНОЙ ФУНКЦИИ
Если функция x=f-1(y) является обратной для функции y=f(x) ,
то функция y=f(x) будет обратной для функции x=f-1(y) .
Т.е. функции y=f(x) и x=f-1(y) являются взаимно обратными.
Область определения функции y=f(x) является множеством значений функции x=f-1(y), а множество значений функции y=f(x) - областью определения функции x=f-1(y)
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости OXY
Слайд 12

Слайд 13
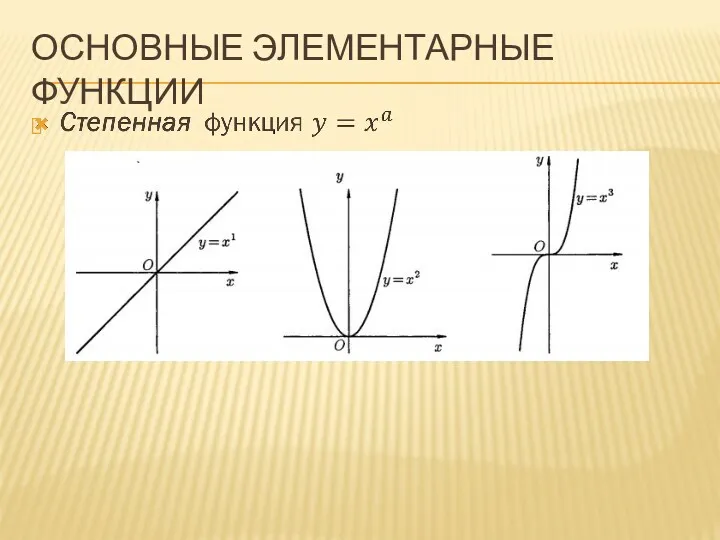
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Слайд 14
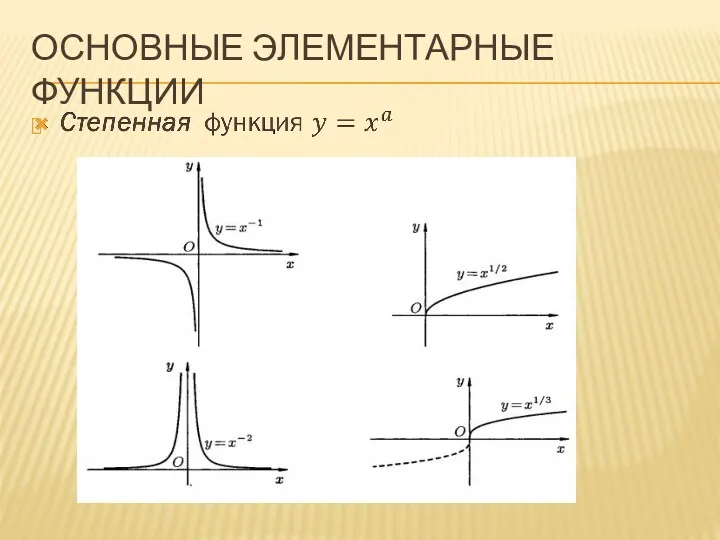
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Слайд 15

ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Слайд 16
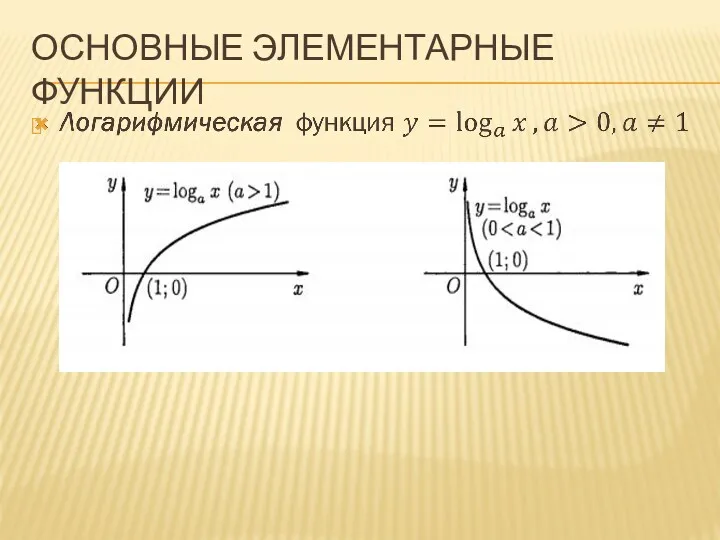
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Слайд 17
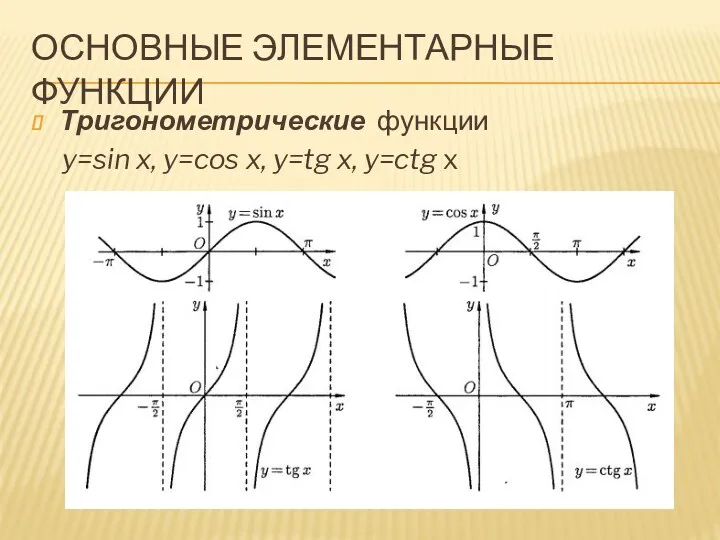
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Тригонометрические функции
y=sin x, y=cos x, y=tg x, y=ctg
x
Слайд 18
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
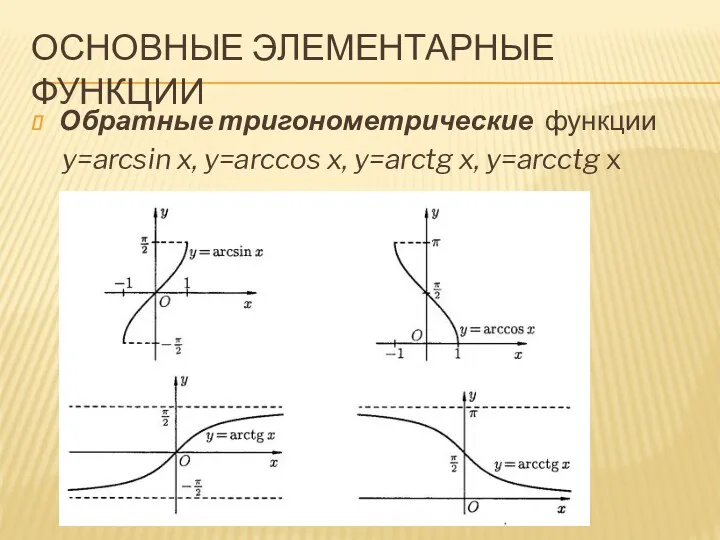
Обратные тригонометрические функции
y=arcsin x, y=arccos x, y=arctg x,
y=arcctg x
Слайд 19

Слайд 20

ПРЕДЕЛ ФУНКЦИИ (ПО ГЕЙНЕ)
Слайд 21

ГЕНРИХ ЭДУАРД ГЕЙНЕ (HEINRICH EDUARD HEINE)
(1821-1881) — немецкий математик. Ученик Дирихле.
Изучал
математику в Гёттингенском университете, Берлинском университете и в Альбертине в Кёнигсберге, был профессором математики
в Бонне и в Галле.
Занимался теорией потенциала, теорией функций и дифференциальными уравнениями
Слайд 22

Слайд 23

ПРЕДЕЛ ФУНКЦИИ (ОБОБЩЕНИЕ ДЛЯ ∞)
Слайд 24
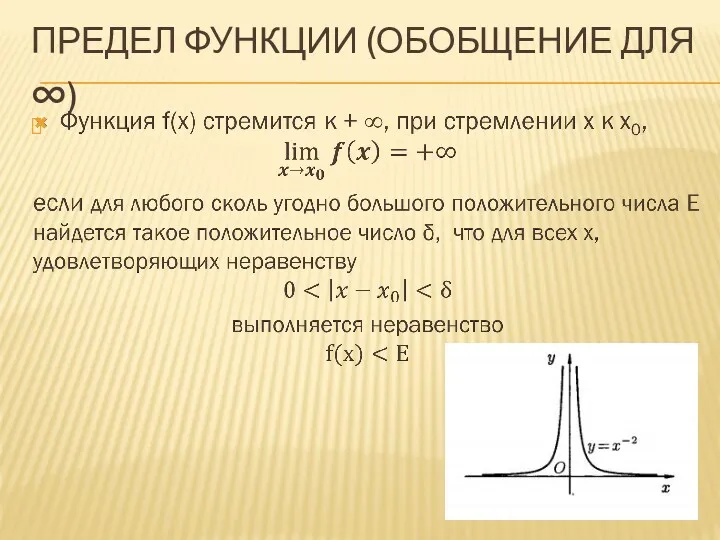
ПРЕДЕЛ ФУНКЦИИ (ОБОБЩЕНИЕ ДЛЯ ∞)
Слайд 25

Слайд 26

Слайд 27

Слайд 28

ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ
Слайд 29

СЛЕДСТВИЯ ТЕОРЕМ О ПРЕДЕЛАХ ФУНКЦИЙ
Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Слайд 35

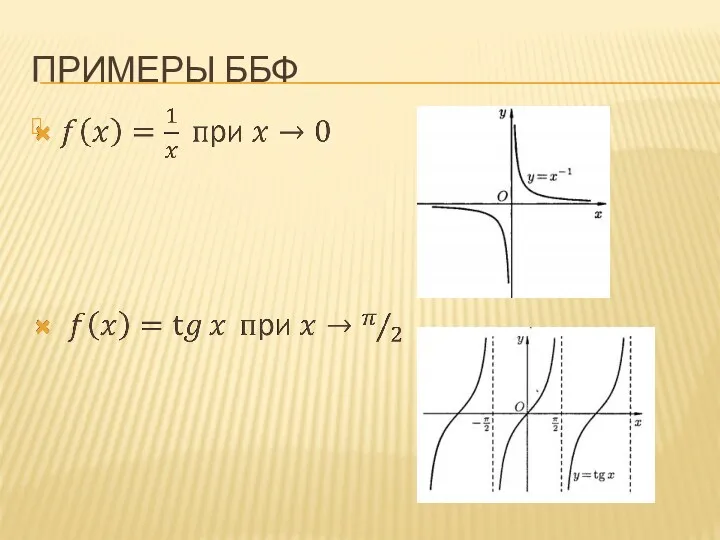
БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
Слайд 36
Слайд 37

Слайд 38
Слайд 39

ТЕОРЕМЫ О БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЯХ
Слайд 40

СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
Две БМФ сравниваются между собой с помощью их
отношения.
Как известно, сумма, разность и произведение двух БМФ. есть БМФ. Отношение же двух БМФ может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Слайд 41

СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ
Слайд 42

ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
Слайд 43

ОСНОВНЫЕ ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ










































 Урок математики. Неравенства. Решение задач. 2 класс, Гармония
Урок математики. Неравенства. Решение задач. 2 класс, Гармония Преобразование выражений. 7 класс
Преобразование выражений. 7 класс Математическая игра Смекай, отгадывай, считай
Математическая игра Смекай, отгадывай, считай Правило сложения отрицательных чисел
Правило сложения отрицательных чисел Переместительное свойство умножения
Переместительное свойство умножения Надання невідкладної медичної допомоги постраждалим
Надання невідкладної медичної допомоги постраждалим Математический язык
Математический язык Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс Действия с многозначными числами
Действия с многозначными числами Презентация КВН Математика - царица всех наук.22.01.2016
Презентация КВН Математика - царица всех наук.22.01.2016 Случаи вычитания 13-
Случаи вычитания 13- Урок математике Хочу всё знать!
Урок математике Хочу всё знать! Аксиомы, теоремы и формулы теории вероятностей
Аксиомы, теоремы и формулы теории вероятностей Презентация Знакомство с задачей 1 класс
Презентация Знакомство с задачей 1 класс Площадь фигуры
Площадь фигуры Единица длины дециметр
Единица длины дециметр Решение заданий №1 по материалам открытого банка задач ЕГЭ по математике 2015 года
Решение заданий №1 по материалам открытого банка задач ЕГЭ по математике 2015 года Пирамида
Пирамида Тема урока: Складываем двузначные числа
Тема урока: Складываем двузначные числа Арифметическая прогрессия
Арифметическая прогрессия Свойства функций
Свойства функций Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82
Обчислення виду 18 – 5. Складання за малюнком задачі на знаходження суми та задачі на різницеве порівняння. Урок №82 Дидактическая игра для детей среднего дошкольного возраста Пятый лишний.
Дидактическая игра для детей среднего дошкольного возраста Пятый лишний. Площадь трапеции. Геометрия. 8 класс
Площадь трапеции. Геометрия. 8 класс Презентация по геометрии Геометрические построения для 7 класса
Презентация по геометрии Геометрические построения для 7 класса Статистика о вреде курения
Статистика о вреде курения Решение уравнений sinx=a. Понятие арксинуса числа
Решение уравнений sinx=a. Понятие арксинуса числа Зручний спосіб обчислення. Віднімання двоцифрових чисел. Задача на різницеве порівняння. Урок №127
Зручний спосіб обчислення. Віднімання двоцифрових чисел. Задача на різницеве порівняння. Урок №127