Содержание
- 2. Игра - молчанка.
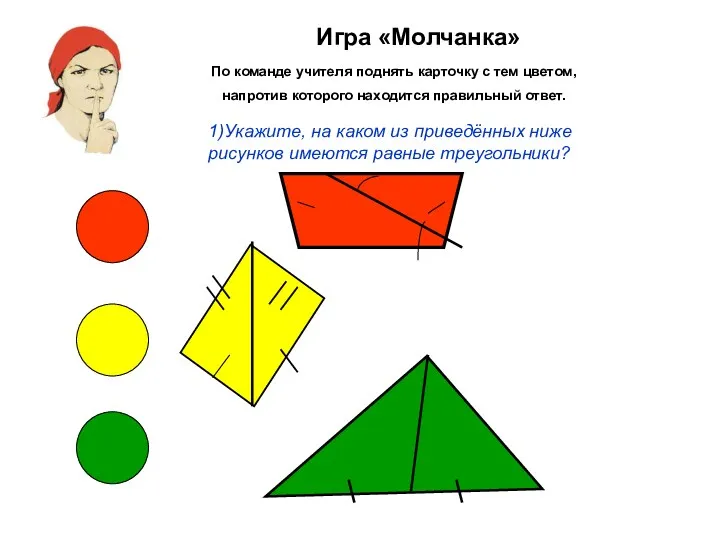
- 3. Игра «Молчанка» По команде учителя поднять карточку с тем цветом, напротив которого находится правильный ответ. 1)Укажите,
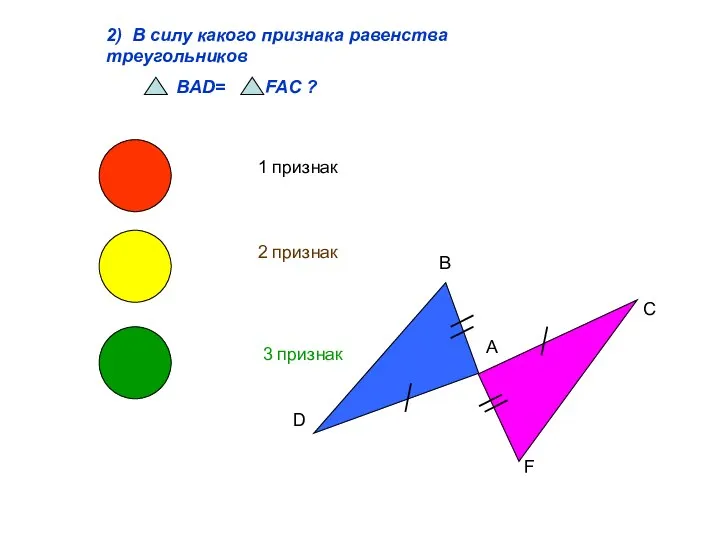
- 4. 2) В силу какого признака равенства треугольников BAD= FAC ? 1 признак 2 признак 3 признак
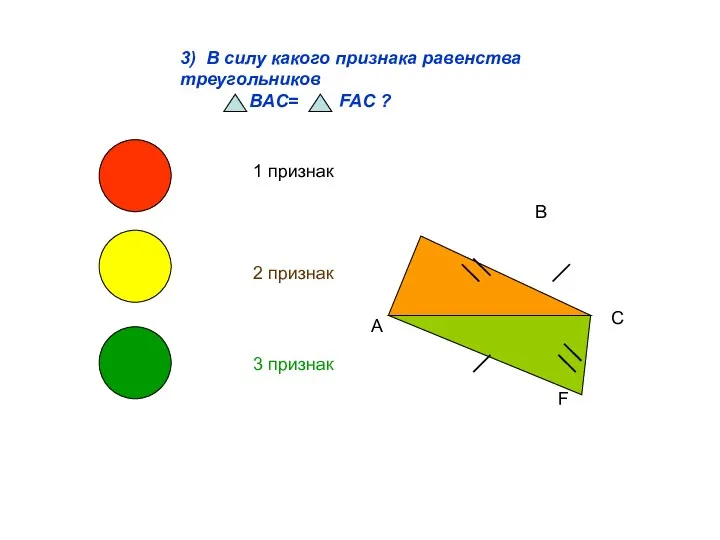
- 5. 3) В силу какого признака равенства треугольников BAC= FAC ? 1 признак 2 признак 3 признак
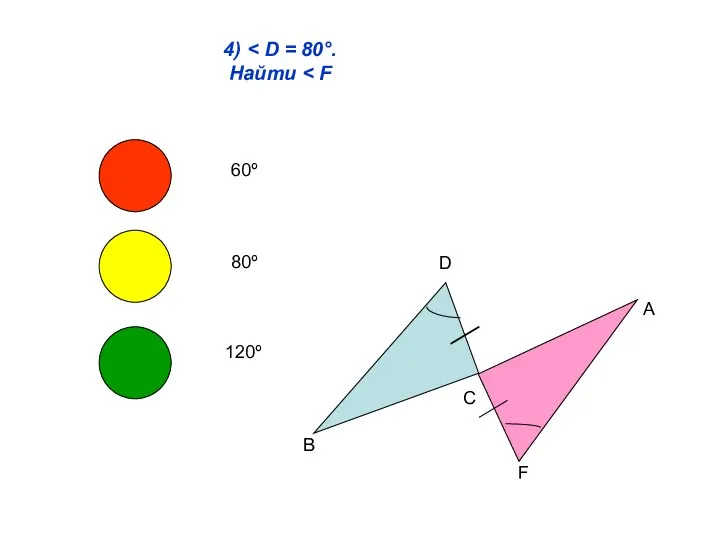
- 6. 4) Найти D B C A F 60º 80º 120º
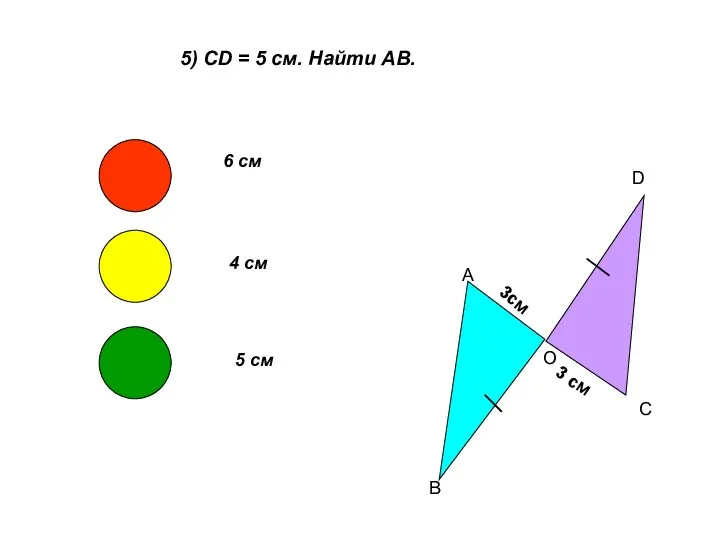
- 7. 5) CD = 5 см. Найти АВ. А В О D C 3см 3 см 6
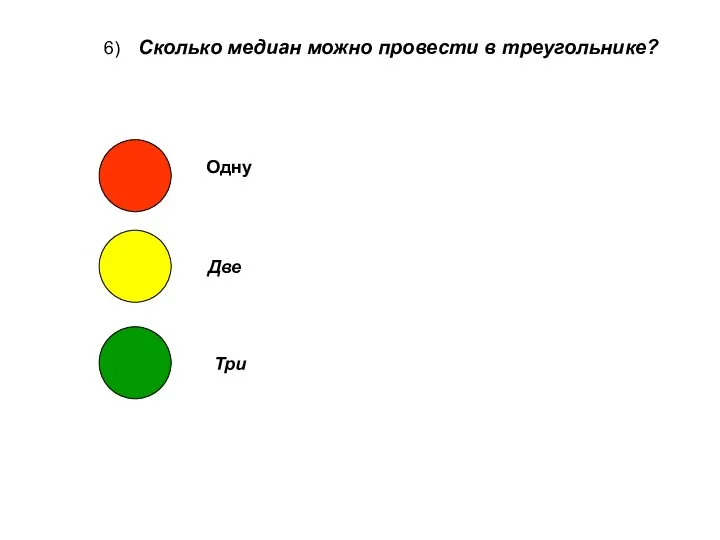
- 8. 6) Сколько медиан можно провести в треугольнике? Одну Две Три
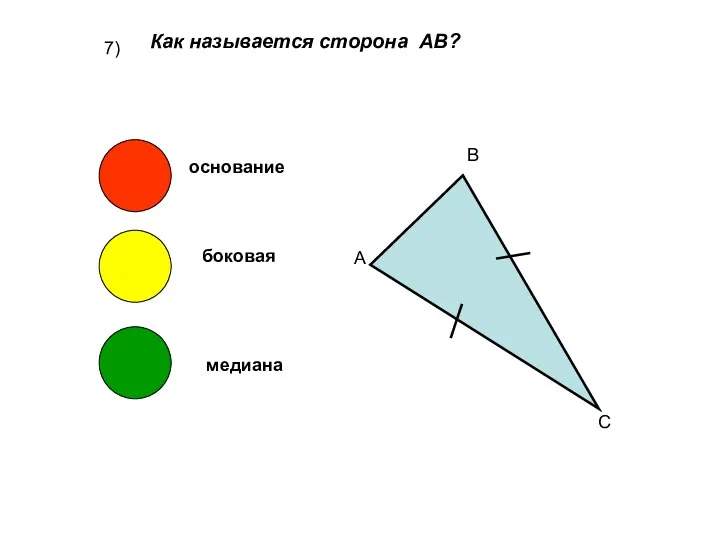
- 9. 7) Как называется сторона АВ? А В С основание боковая медиана
- 10. Отметь знаком «+» правильные утверждения и знаком «-» - ошибочные. 1) Окружностью называется фигура, состоящая из
- 11. Построения циркулем и линейкой
- 12. В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и
- 13. Неразрешимые задачи Следующие три задачи на построение были поставлены ещё в античности: Трисекция угла — разбить
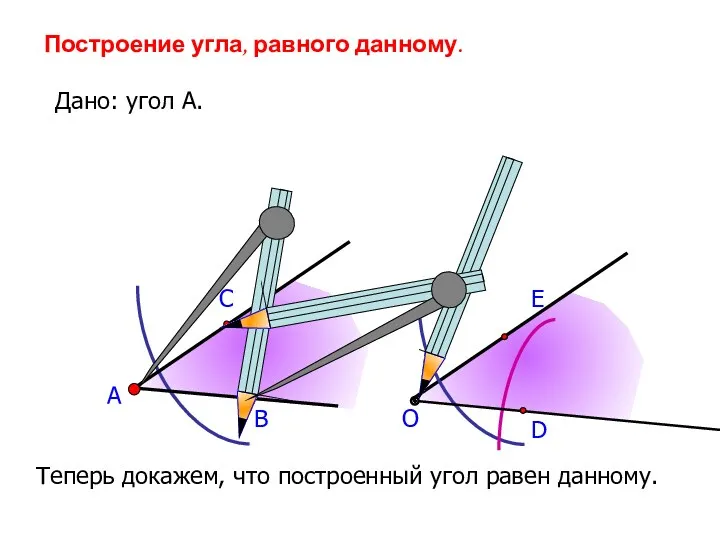
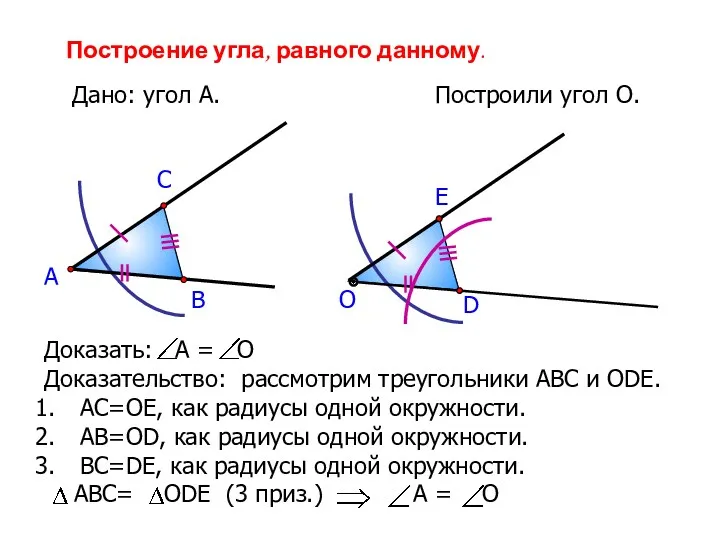
- 14. А В С Построение угла, равного данному. Дано: угол А. О D E Теперь докажем, что
- 15. Построение угла, равного данному. Дано: угол А. А Построили угол О. В С О D E
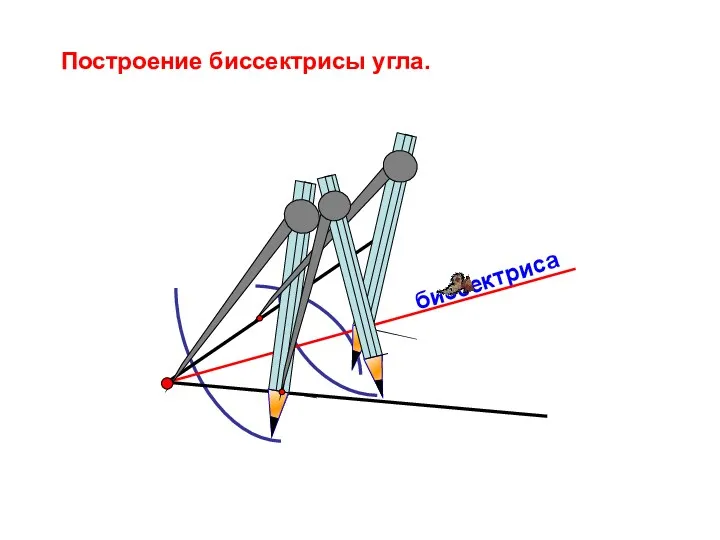
- 16. биссектриса Построение биссектрисы угла.
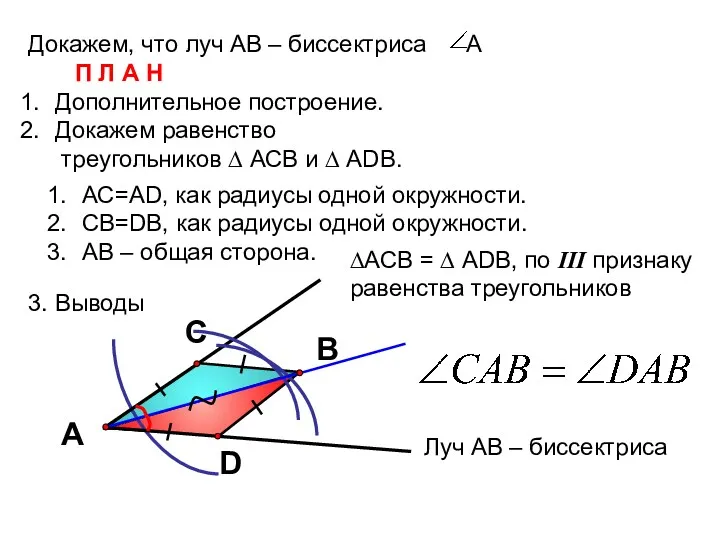
- 17. Докажем, что луч АВ – биссектриса А П Л А Н Дополнительное построение. Докажем равенство треугольников
- 18. Решение упражнений. Рабочая тетрадь № 79. (стр.33)
- 19. Постройте луч ОС так, чтобы луч ОА был биссектрисой угла ВОС. Р е ш е н
- 20. Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить
- 21. Л. Москерони Якоб Штейнер Понселе Жан Виктор
- 22. Домашнее задание. № 155 учебник (стр. 155), 154 а)
- 24. Скачать презентацию










 Сложные события
Сложные события Совершенствование навыка решения текстовых задач.
Совершенствование навыка решения текстовых задач. Дәрес планы
Дәрес планы Презентация Устный счёт 2 класс 1 четверть № 1
Презентация Устный счёт 2 класс 1 четверть № 1 Сложение числа б с однозначными числами. 1 класс
Сложение числа б с однозначными числами. 1 класс Статистическое распределение выборки и его основные числовые характеристики
Статистическое распределение выборки и его основные числовые характеристики Умножение однозначных чисел на многозначные
Умножение однозначных чисел на многозначные Софизмы и парадоксы. 10 класс
Софизмы и парадоксы. 10 класс Построение и выбор аналитических моделей
Построение и выбор аналитических моделей Комплексні числа
Комплексні числа Столбчатая диаграмма
Столбчатая диаграмма Производная показательной, логарифмической и степенной функций при подготовке к ЕГЭ по математике
Производная показательной, логарифмической и степенной функций при подготовке к ЕГЭ по математике Презентация к конспекту НОД по теме: В поисках сюрприза
Презентация к конспекту НОД по теме: В поисках сюрприза Письменные приемы деления многозначных чисел на двузначное число 4 класс
Письменные приемы деления многозначных чисел на двузначное число 4 класс Как устроены числа.
Как устроены числа. Экономико-математические методы и модели. Теоремы двойственности
Экономико-математические методы и модели. Теоремы двойственности Делители и кратные
Делители и кратные Состав чисел второго десятка
Состав чисел второго десятка Задачи на построение сечений. Урок геометрии в 10 классе
Задачи на построение сечений. Урок геометрии в 10 классе Элементы теории множеств. Понятие множества
Элементы теории множеств. Понятие множества Метод наименьших квадратов (МНК)
Метод наименьших квадратов (МНК) Делители и кратные
Делители и кратные Натуральные числа
Натуральные числа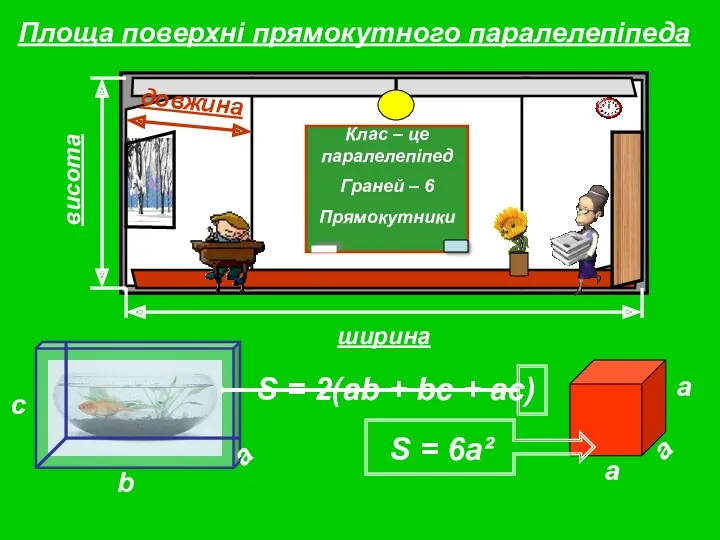 Площа поверхні прямокутного паралелепіпеда
Площа поверхні прямокутного паралелепіпеда Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Презентация у уроку математики во 2 классе по теме Свойство противоположных сторон прямоугольника
Презентация у уроку математики во 2 классе по теме Свойство противоположных сторон прямоугольника Умножение десятичных дробей
Умножение десятичных дробей Формула разности квадратов
Формула разности квадратов