Содержание
- 2. Лекция 6 Независимые события . 2. Формула полной вероятности. 3. Формула Байеса . Сложные события. Повторение
- 3. Независимые события . События А и В называются независимыми, если вероятность наступления одного из них не
- 4. По формуле умножения вероятностей - вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.
- 5. Вероятность совмещения нескольких независимых событий A1, A2, …, An равна произведению вероятностей этих событий: P(A1 A2
- 6. Пример. Три стрелка: вероятность поражения цели при одном выстреле каждым стрелком. Все стреляют по одному разу.
- 7. - события независимые.
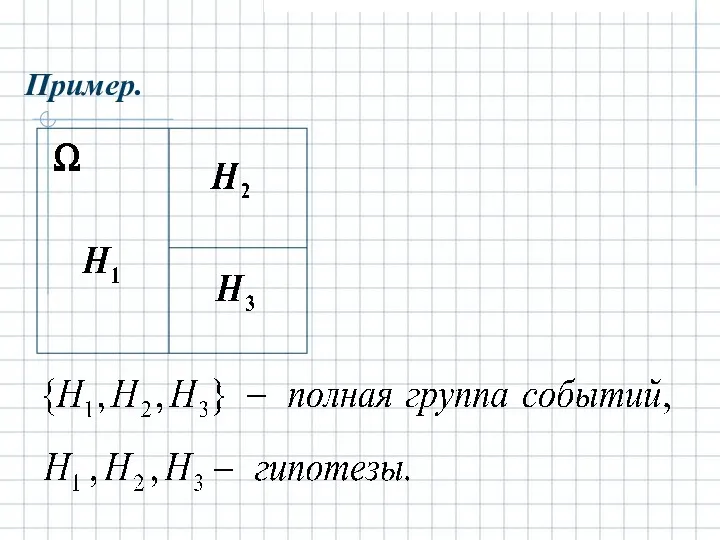
- 8. Пусть - множество всех элементарных исходов, H1, H2, … ,Hn – наблюдаемые события. Формула полной вероятности.
- 9. Пример.
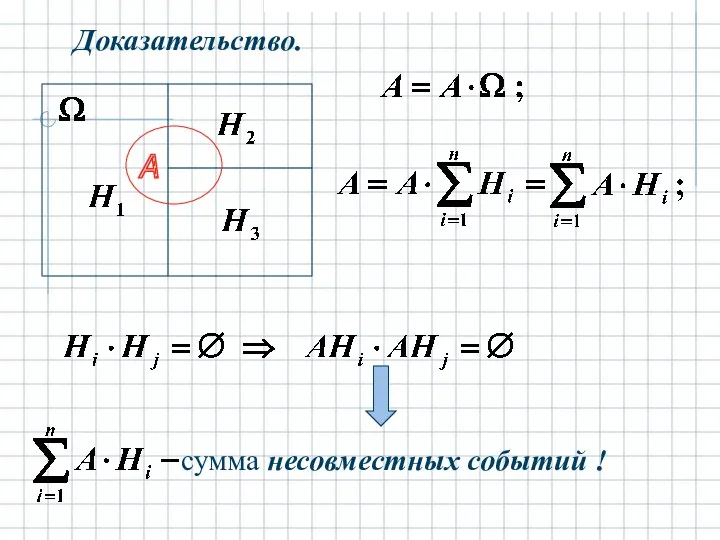
- 10. то для любого наблюдаемого события А справедлива формула (формула полной вероятности) : причём
- 11. Доказательство. A сумма несовместных событий !
- 12. Вероятность суммы несовместных событий равна сумме вероятностей: Пример. В ящике М шаров, из них m –
- 13. Решение. { 1й шар - белый}. { 1й шар - чёрный}.
- 14. Формула Байеса .
- 15. Пусть проводится некоторый опыт, об условиях проведения которого можно высказать n возможных и несовместных гипотез, имеющих
- 16. Как изменятся вероятности гипотез, если стало известно, что событие А произошло ? Иначе говоря, спрашивается, чему
- 17. Если до опыта вероятности гипотез были P(H1), P(H2), … , P(Hn) и в результате опыта произошло
- 18. В этой формуле в знаменателе стоит полная вероятность события А:
- 19. Доказательство.
- 20. Пример. Имеются 1000 изделий, из которых 200 изготовлены на 1-м заводе, 460 на втором и 340
- 21. Решение. А= {взятое изделие оказалось нестандартным}. {оно сделано на 1-м заводе}. {оно слелано на 2-м заводе}.
- 23. Повторение независимых испытаний. Формула Бернулли. Пусть вероятность наступления события А при одном испытании равна P(A) =
- 24. Теорема. Вероятность того, что при n- независимых испытаниях событие А произойдёт m- раз определяется формулой (формула
- 25. Доказательство. Наступления (А) и не наступления события А в серии из n- испытаний могут чередоваться различным
- 26. Всякую комбинацию из n- испытаний, в которую событие А входит m- раз,а событие входит, следовательно, (n-m)
- 27. Например, Эта комбинация соответствует событию В={Cобытие А произошло в m испытаниях}. Возможна другая комбинация для события
- 28. Общее количество исходов N,образующих множество В, равно числу cпособов выбрать m чисел из n, т.е. равно
- 29. Таким образом, Вычислим вероятность события В. Вычислим вероятность одной комбинации (например В1):
- 30. Таким образом, Окончательно, -Формула Бернулли для вычисления вероятности события: в последовательности из n испытаний m раз
- 31. Событие А произошло т раз в п испытаниях - вероятность того, что в п испытаниях событие
- 32. Пример. Что вероятнее: выиграть у равного по силам партнера игру из 4х или из 8 партий?
- 35. Длина отрезка Вывод: Наивероятнейших чисел не может быть больше двух. Два будет в случае попадания концов
- 36. Пример. Игра из 4х партий. Решение.
- 38. Скачать презентацию









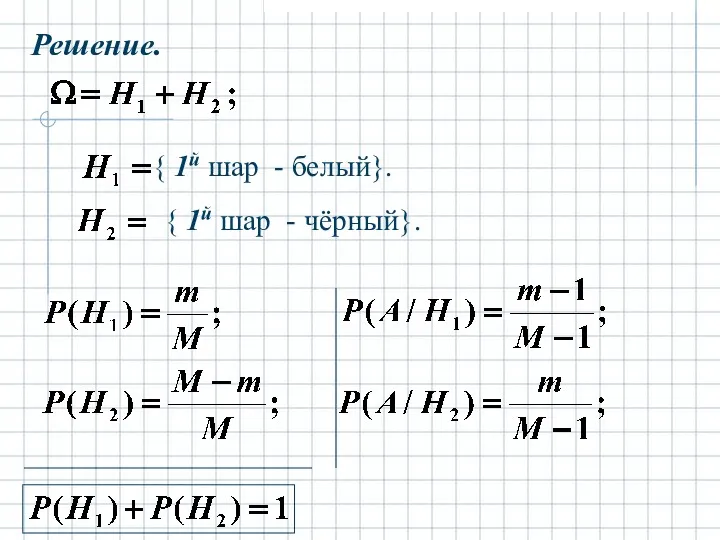








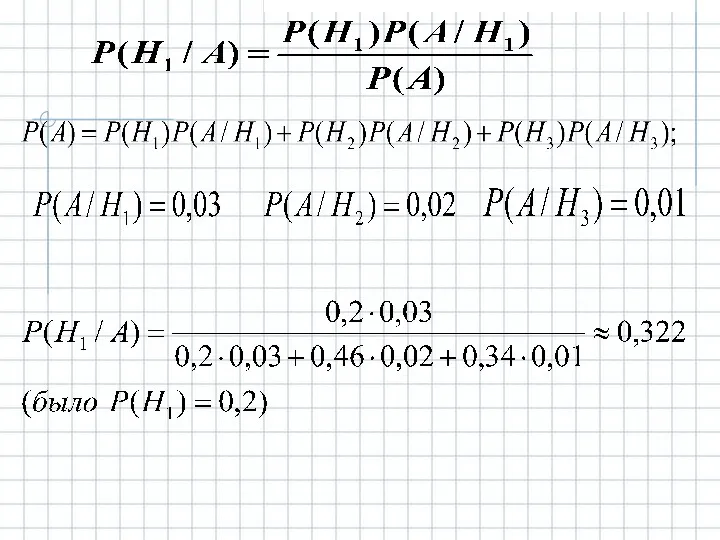





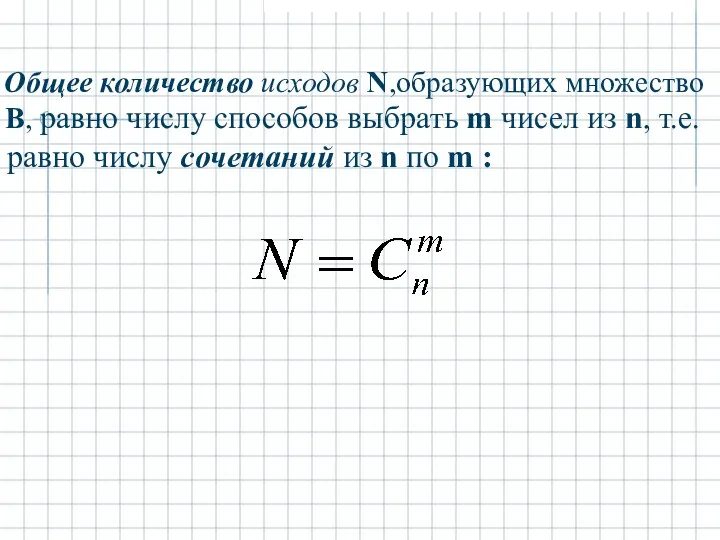




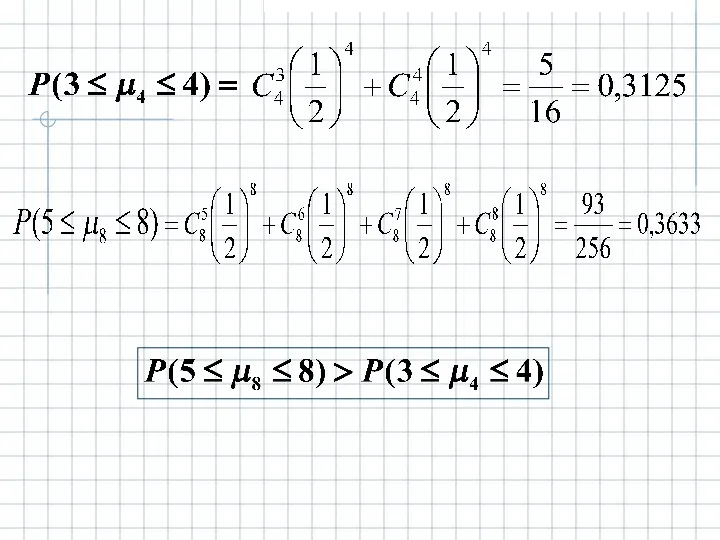



 Применение нескольких способов разложения многочленов на множители
Применение нескольких способов разложения многочленов на множители The mean
The mean Практическое применение интегралов в различных областях
Практическое применение интегралов в различных областях Действия с десятичными дробями
Действия с десятичными дробями Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса
Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса Умножение числа 6
Умножение числа 6 вектор в математике и физике
вектор в математике и физике Решение уравнений. Устный счет
Решение уравнений. Устный счет Параллелепипед. Грани, ребра, диагональ параллелепипеда
Параллелепипед. Грани, ребра, диагональ параллелепипеда Умножение чисел с разными знаками. 6 класс
Умножение чисел с разными знаками. 6 класс Прямоугольный треугольник
Прямоугольный треугольник Интегрированный урок (математика + письмо) Уроки в Простоквашино
Интегрированный урок (математика + письмо) Уроки в Простоквашино Все действия с рациональными числами
Все действия с рациональными числами Интерактивный тест по математике Геометрические фигуры 2 класс
Интерактивный тест по математике Геометрические фигуры 2 класс Усна лічба Ланцюжок
Усна лічба Ланцюжок Умножение одночленов
Умножение одночленов Виды треугольников
Виды треугольников Сложение чисел с разными знаками
Сложение чисел с разными знаками Умножение и деление чисел
Умножение и деление чисел Двузначные числа в случае, когда сумма – круглое число
Двузначные числа в случае, когда сумма – круглое число Теория графов
Теория графов Определение направляющих косинусов. Связь координат соответственных точек местности и снимка
Определение направляющих косинусов. Связь координат соответственных точек местности и снимка Сумма углов треугольника
Сумма углов треугольника Взаимное расположение прямых в пространстве. Угол между прямыми
Взаимное расположение прямых в пространстве. Угол между прямыми презентация Веселая неделя
презентация Веселая неделя Деление с остатком- презентация Диск
Деление с остатком- презентация Диск Презентация к уроку математики Числа от 10 до 20
Презентация к уроку математики Числа от 10 до 20 Модуль числа. Классная работа
Модуль числа. Классная работа