Содержание
- 2. Основные вопросы лекции. Введение Понятие графа.
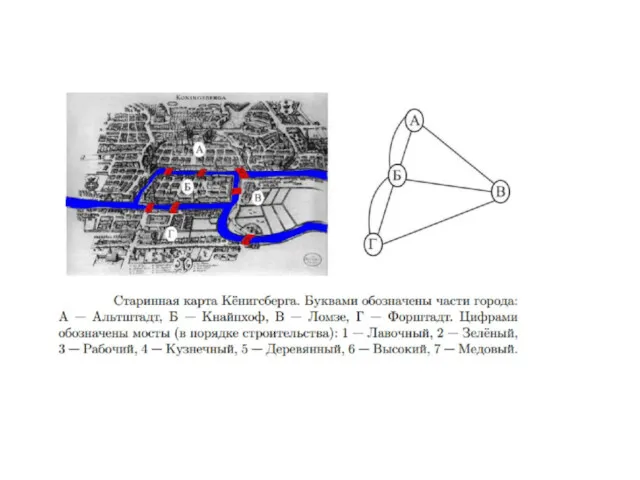
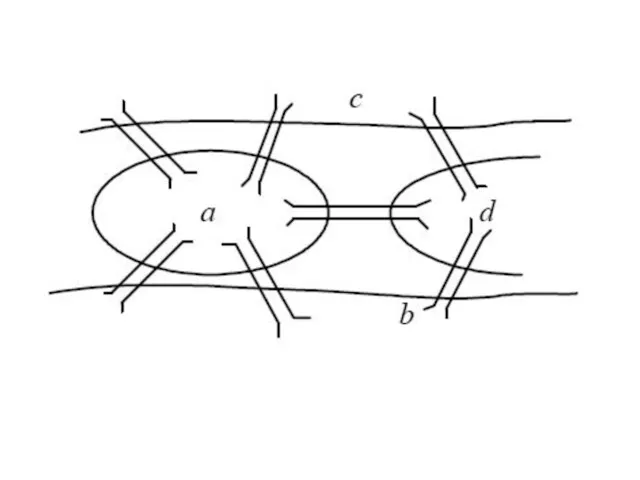
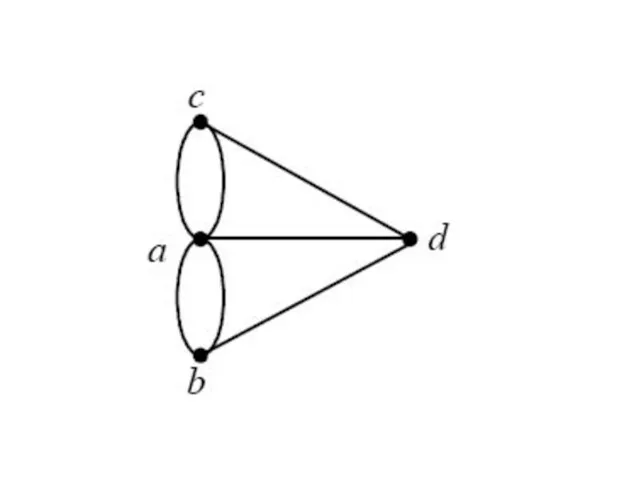
- 3. Первая работа по графам была опубликована математиком Эйлером в 1736 году. Она содержала решение задачи о
- 7. Начало развития теории графов как самостоятельной математической дисциплины положено Д. Кенигом, выпустившим в 1936 году книгу
- 8. Преимущество графов следует из того, что они однозначно описывают структуру системы, на их основе просто записываются
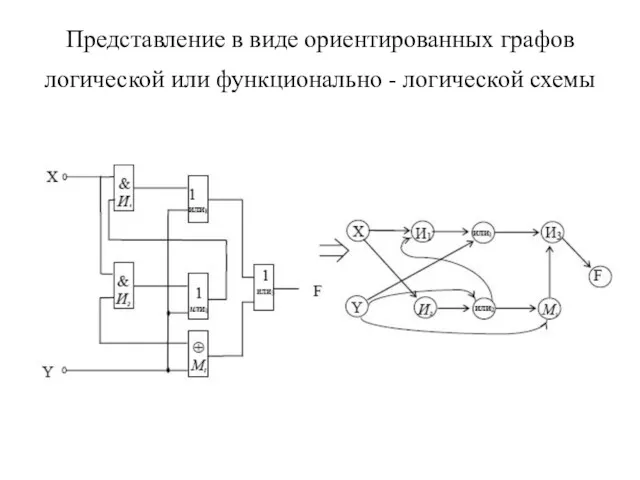
- 9. Представление в виде ориентированных графов логической или функционально - логической схемы
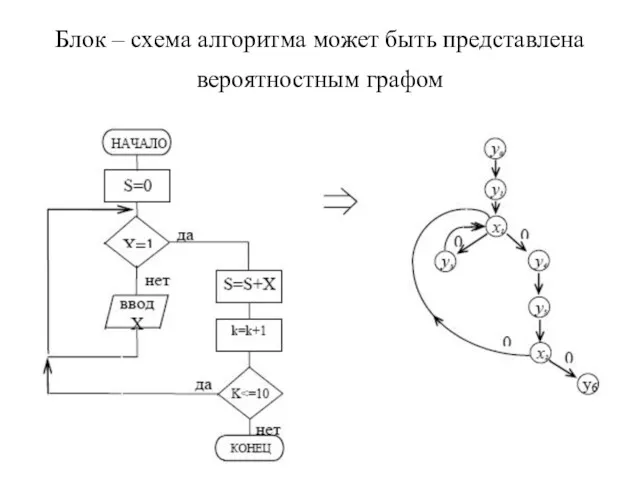
- 10. Блок – схема алгоритма может быть представлена вероятностным графом
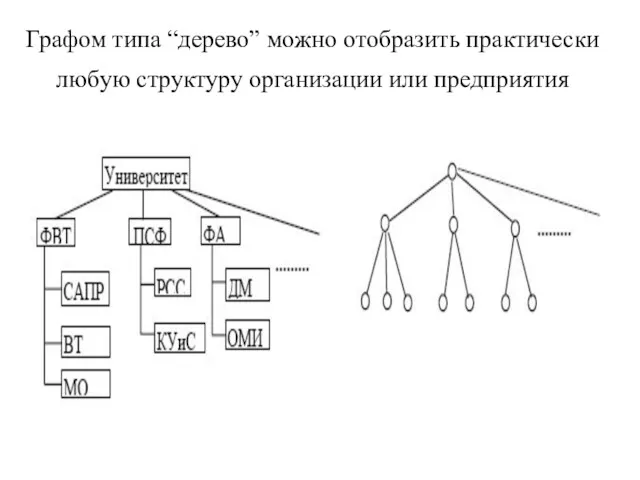
- 11. Графом типа “дерево” можно отобразить практически любую структуру организации или предприятия
- 12. Граф есть конечное множество V, называемое множеством вершин, на котором задано симметричное, антирефлексивное отношение R и
- 13. Множество Е называется множеством ребер. Всякий элемент множества Е называется ребром. Граф обозначается G(V, E). Элементы
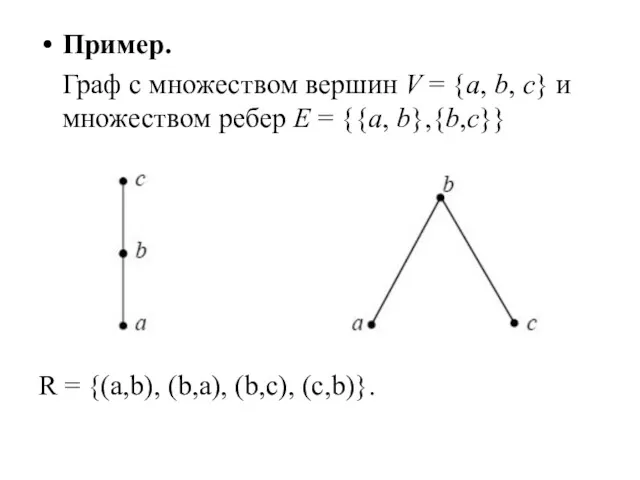
- 14. Пример. Граф с множеством вершин V = {a, b, c} и множеством ребер Е = {{a,
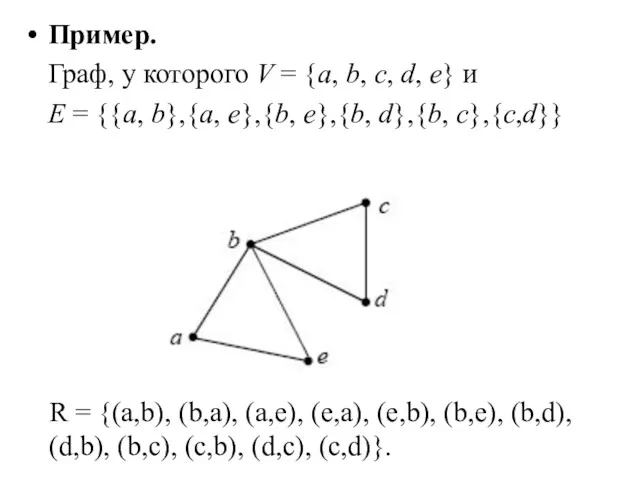
- 15. Пример. Граф, у которого V = {a, b, c, d, e} и Е = {{a, b},{a,
- 16. Для отношения более общего вида необходимо представление элемента (а,b) ∈ R, для которого возможно (b,a) ∉
- 17. Ориентированный граф, или орграф G, обозначаемый G (V,E), состоит из множества V вершин и отношения E
- 18. Элемент множества Е называется ориентированным ребром. Если (a,b) ∈ E, то a называется начальной вершиной (a,b),
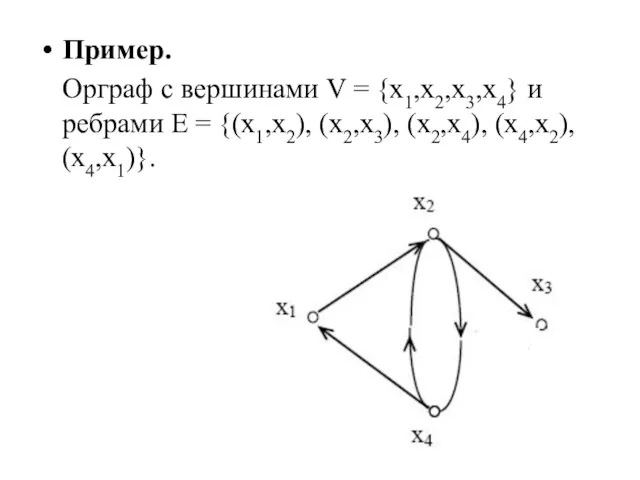
- 19. Пример. Орграф с вершинами V = {x1,x2,x3,x4} и ребрами E = {(x1,x2), (x2,x3), (x2,x4), (x4,x2), (x4,x1)}.
- 20. Замечания: Ребро орграфа обозначается на диаграмме стрелкой от a к b и называется дугой. В простом
- 21. Граф есть конечное множество V, называемое множеством вершин, и множество Е двухэлементных всех неупорядоченных различных подмножеств
- 22. Граф G (V,E) – комбинаторный объект, состоящий из двух конечных множеств: V – называемого множеством вершин
- 23. Конечный граф с n вершинами называется графом n-го порядка.
- 24. Если {a, b} – ребро, тогда вершины a и b называются концами ребра {a, b}. Ребро
- 25. Две вершины называются смежными, если они являются концами ребра, или, что то же самое, если они
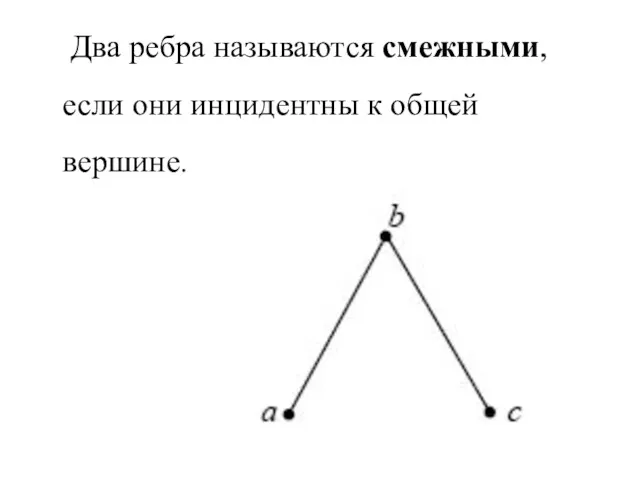
- 26. Два ребра называются смежными, если они инцидентны к общей вершине.
- 27. Граф G (V,E) – совокупность двух множеств: вершин V и ребер E, между которыми определено отношение
- 28. Ребро, которое соединяет вершину саму с собой, называется петлей. Ребро, которому поставлена в соответствие пара вида
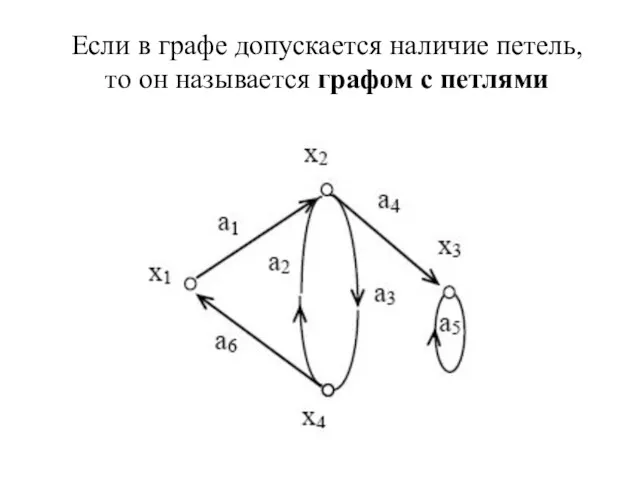
- 29. Если в графе допускается наличие петель, то он называется графом с петлями
- 30. В графе антирефлексивного и симметричного отношения нет петель и для каждой пары вершин либо нет ни
- 31. Если в таком графе каждую пару ориентированных ребер, соединяющих одни и те же две вершины, заменить
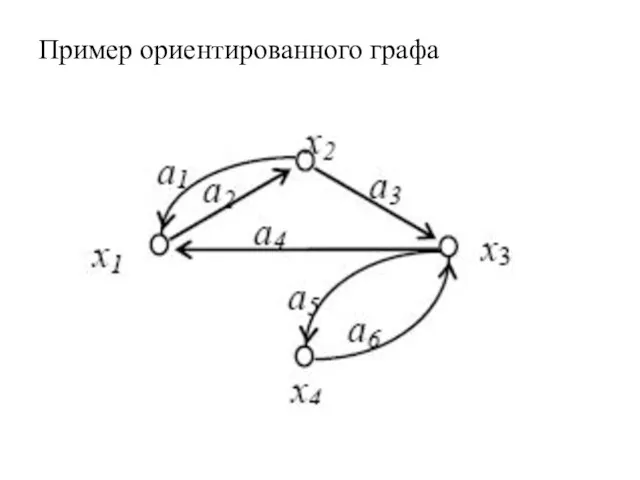
- 32. Пример ориентированного графа
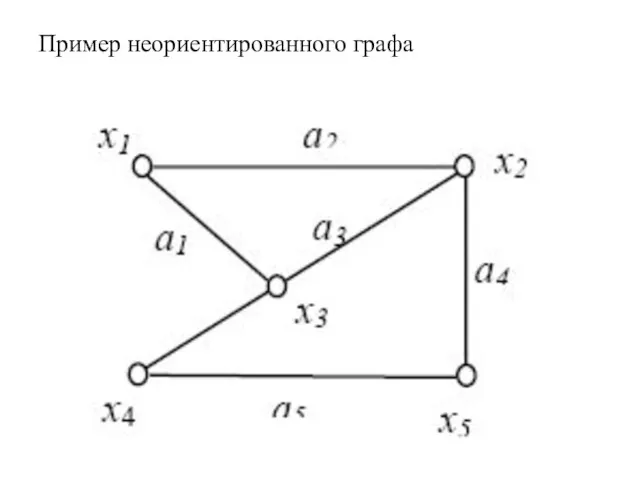
- 33. Пример неориентированного графа
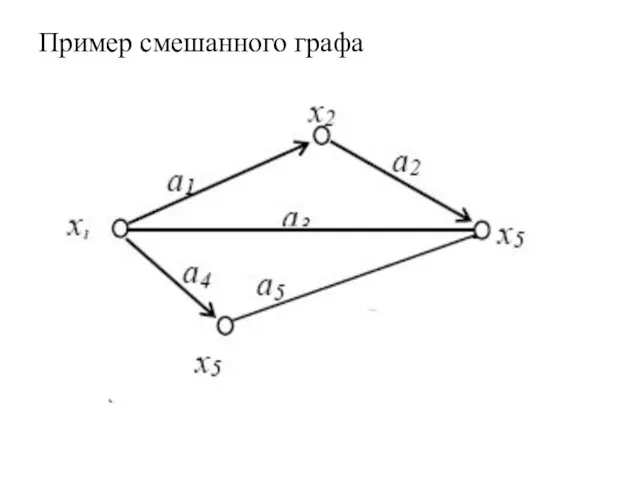
- 34. Пример смешанного графа
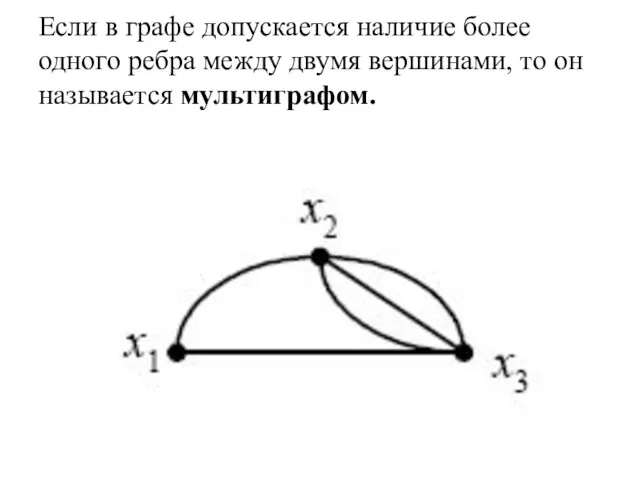
- 35. Если в графе допускается наличие более одного ребра между двумя вершинами, то он называется мультиграфом.
- 36. Если G(V, E) – мультиграф, то Е может иметь несколько ребер (а,b). Такие ребра называются кратными
- 37. Замечания: Граф – это мультиграф, у которого кратность каждого ребра равна единице. В графе две вершины
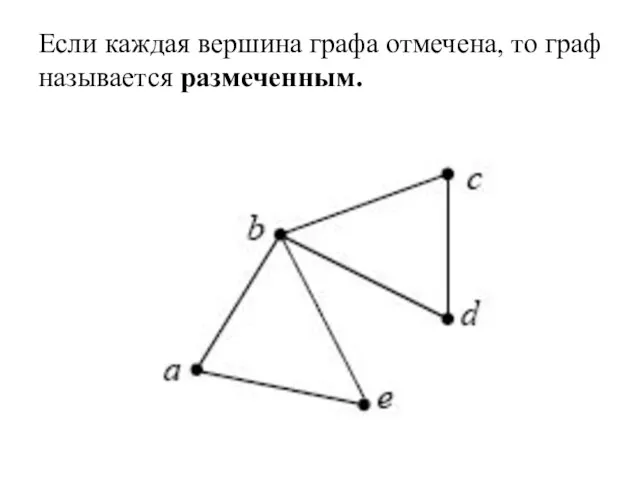
- 38. Если каждая вершина графа отмечена, то граф называется размеченным.
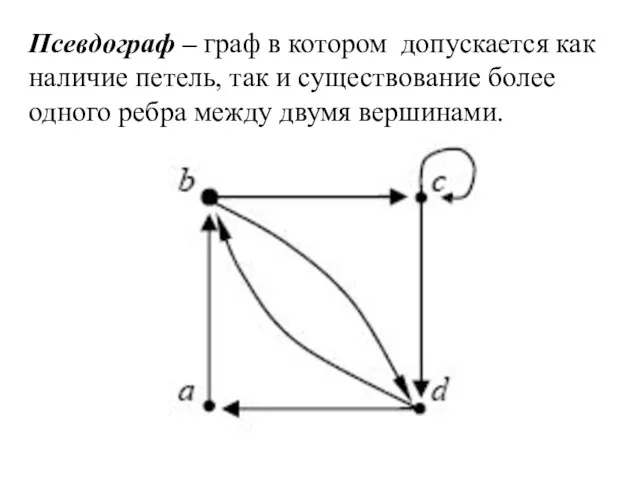
- 39. Псевдограф – граф в котором допускается как наличие петель, так и существование более одного ребра между
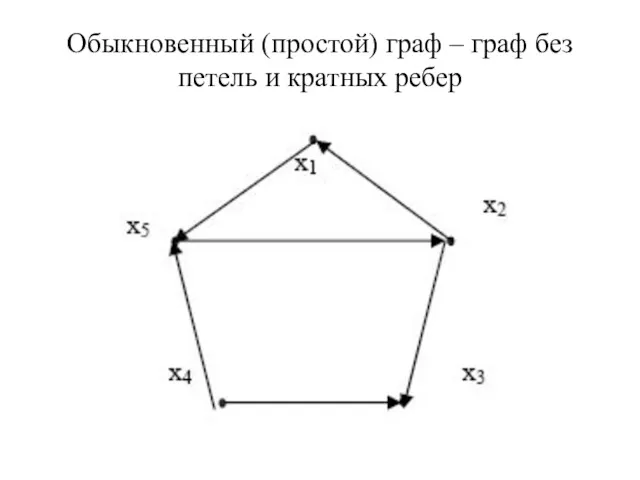
- 40. Обыкновенный (простой) граф – граф без петель и кратных ребер
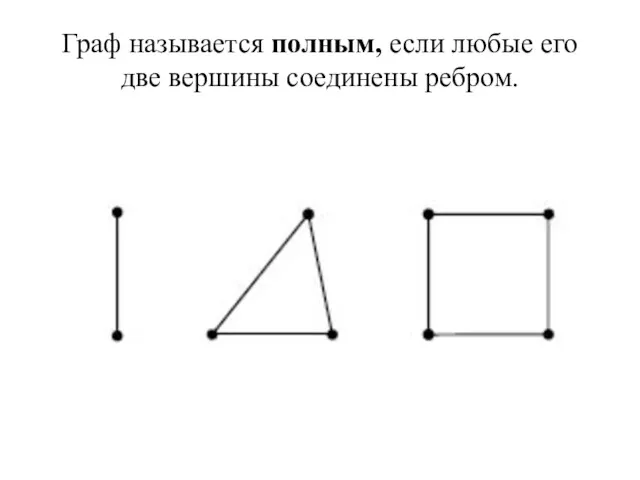
- 41. Граф называется полным, если любые его две вершины соединены ребром.
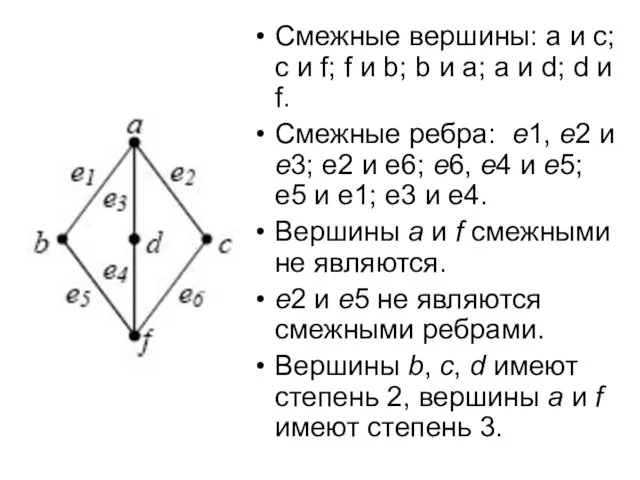
- 42. . Степенью вершины υ, обозначается deg(υ), называется количество ребер, инцидентных этой вершине. Вершина степени 0 называется
- 43. Смежные вершины: а и с; с и f; f и b; b и a; a и
- 44. Лемма о рукопожатии. Сумма степеней всех вершин графа есть четное число.
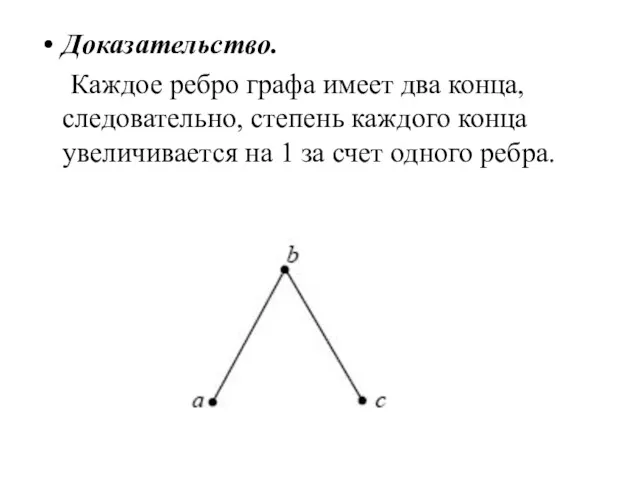
- 45. Доказательство. Каждое ребро графа имеет два конца, следовательно, степень каждого конца увеличивается на 1 за счет
- 46. Таким образом, в сумму степеней всех вершин каждое ребро вносит 2 единицы, поэтому сумма должна в
- 47. Следствие. В любом графе количество вершин нечетной степени четно.
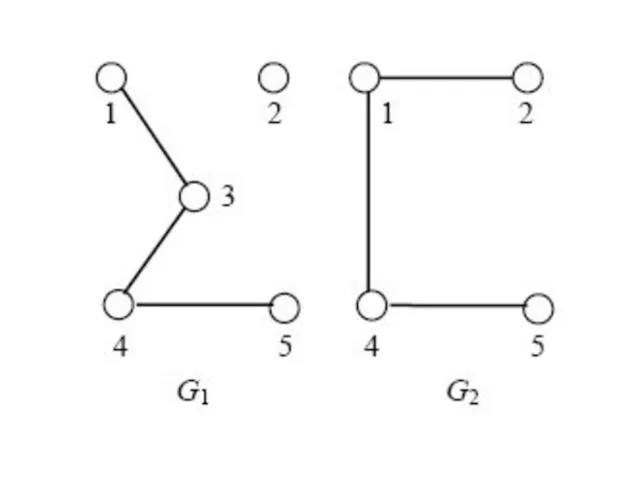
- 48. Граф G ′(V ′, E′) называется подграфом графа G(V, E), обозначается G′(V′, E′) G(V, E), если
- 49. Всякий подграф может быть получен из графа удалением некоторых вершин и ребер.
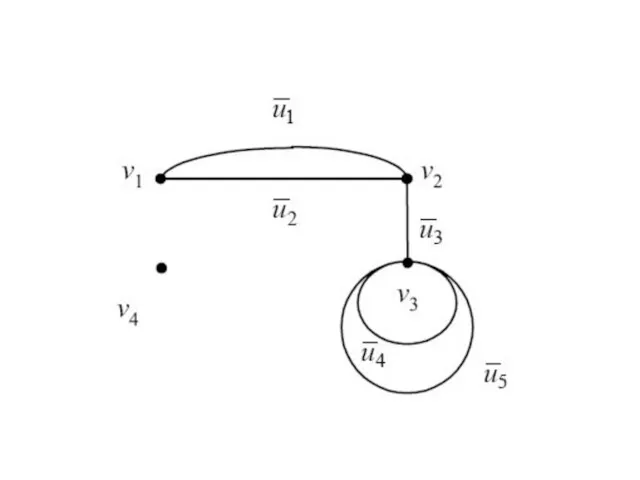
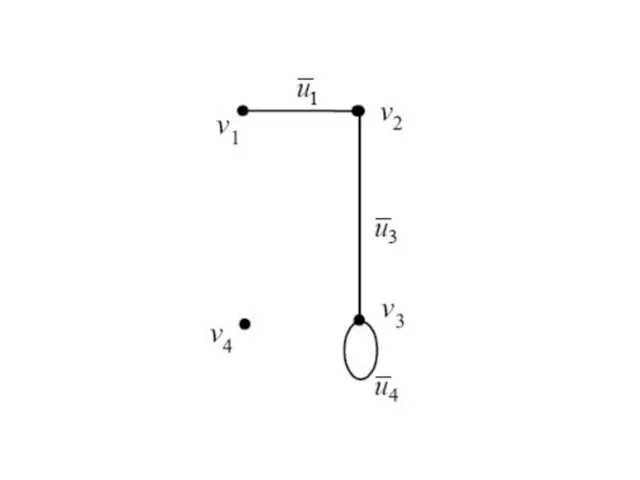
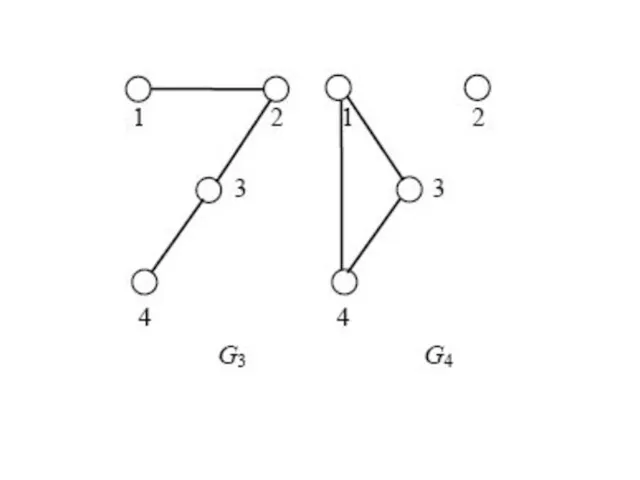
- 50. Суграфом графа G называется граф , где , т.е. суграф получается из исходного графа путем удаления
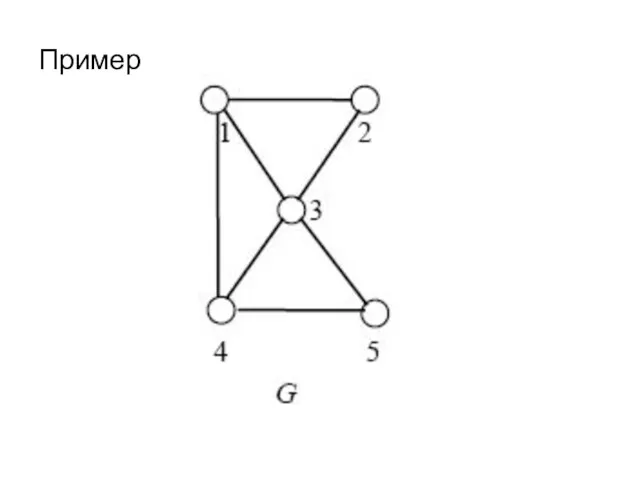
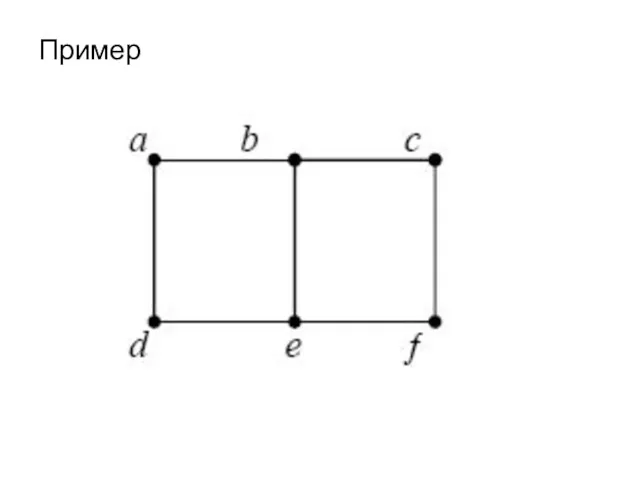
- 53. Пример
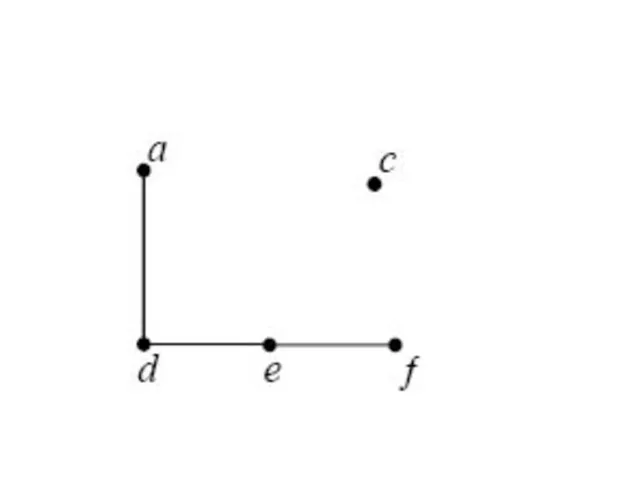
- 56. Пример
- 59. Скачать презентацию




























 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Топқа бөлу
Топқа бөлу Вычисление площадей фигур на клетчатой бумаге
Вычисление площадей фигур на клетчатой бумаге Дифференцированный подход в обучении учащихся при подготовке к ГИА
Дифференцированный подход в обучении учащихся при подготовке к ГИА Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰ Сети и потоки
Сети и потоки Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Синус, косинус, тангенс та котангенс кута
Синус, косинус, тангенс та котангенс кута Сумма углов треугольника
Сумма углов треугольника Нормирование погрешностей средств измерений
Нормирование погрешностей средств измерений Свойства цилиндра. Выпуклый и прямой цилиндр
Свойства цилиндра. Выпуклый и прямой цилиндр Стохастические модели приземных трасс
Стохастические модели приземных трасс Сравнение дробей с разными знаменателями. 6 класс
Сравнение дробей с разными знаменателями. 6 класс Признаки делимости
Признаки делимости Изучение величин: объём
Изучение величин: объём Презентация Количественный счет
Презентация Количественный счет Решение задач по теме Многогранники
Решение задач по теме Многогранники Презентация к уроку математики 1 класс
Презентация к уроку математики 1 класс Урок - игра. Тема: Производная и интеграл
Урок - игра. Тема: Производная и интеграл История числа Пи
История числа Пи Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Решение задач в 1-ом классе
Решение задач в 1-ом классе Незнайкины задачки. Математика. 1 класс
Незнайкины задачки. Математика. 1 класс Действия с десятичными дробями
Действия с десятичными дробями Системы дифференциальных уравнений
Системы дифференциальных уравнений Геометрии Евклида как первая научная система
Геометрии Евклида как первая научная система Первый признак подобия треугольников
Первый признак подобия треугольников Степенные функции, их свойства и графики
Степенные функции, их свойства и графики