Содержание
- 2. ОПРЕДЕЛЕНИЯ Нормированное пространство, Х – это упорядоченная пара , где || . || - норма в
- 3. ПРИМЕРЫ НОРМ 1.X=B[a, b] ( X=C[a, b]) 2. X=L1[a, b] 3. X=L2[a, b] 4. X=l1
- 4. ПРИМЕРЫ НОРМ 5. X=l2. 6. X=Rn; Cn. 7. Х- л.п. ограниченных последовательностей
- 5. ПРИМЕРЫ НА ВЫЧИСЛЕНИЕ НОРМЫ
- 7. МЕТРИЧЕСКАЯ СТРУКТУРА Н.П. Метрика в н.п.Х – неотрицательная функция d(x,y) = || x - y ||
- 8. ПРИМЕРЫ СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Cходится ли к x0(t)≡0 в н.п. X ? 1. X=C[0,1], не сходится 2.
- 9. ФУНДАМЕНТАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ОПРЕДЕЛЕНИЕ Последовательность {xn } называется фундаментальной, если при ∀ n,m → ∞ ⇒ d(xn
- 10. ПРИМЕРЫ БАНАХОВЫХ ПРОСТРАНСТВ
- 11. ПРИМЕР 2.
- 13. ОСНОВНЫЕ УТВЕРЖДЕНИЯ 1) Согласованность линейной и метрической структуры в н.п. 1.1.Алгебраические операции в н.п. непрерывны: если
- 14. НЕРАВЕНСТВА ГЁЛЬДЕРА И МИНКОВСКОГО если (p,q > 1 & 1/p + 1/q = 1 ⇔ p
- 15. КРИТЕРИЙ БАНАХОВОСТИ банахово (1) ⇔ (X - замкнутое п/п в б.п. ) (2) ⇔ (∀ абсолютно
- 16. (X - ЗАМКНУТОЕ П/П В Б.П. ) БАНАХОВО
- 19. Теорема. - банахово пространство.
- 20. СЛЕДСТВИЯ 1) l∞ - б.п.; 2) если T – компактное множество ⇒ - б.п.; 3) C[a,
- 21. Лемма Рисса о почти перпендикуляре. (Пусть X н.п., X ≠ Y-замкнутое п/п в Х, ε>0), тогда
- 22. ПРИМЕРЫ ОГРАНИЧЕННЫХ МНОЖЕСТВ
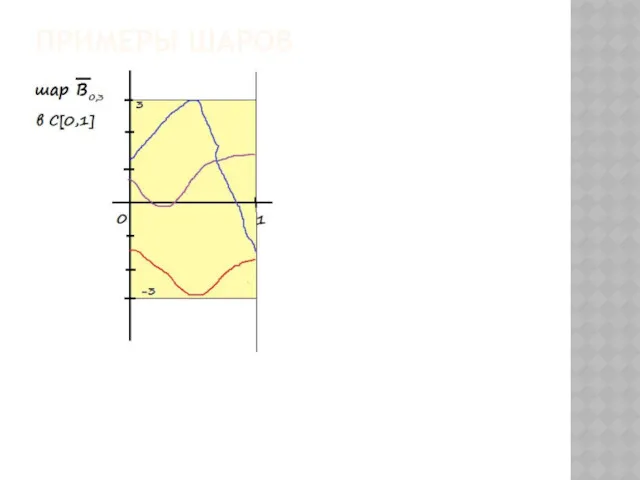
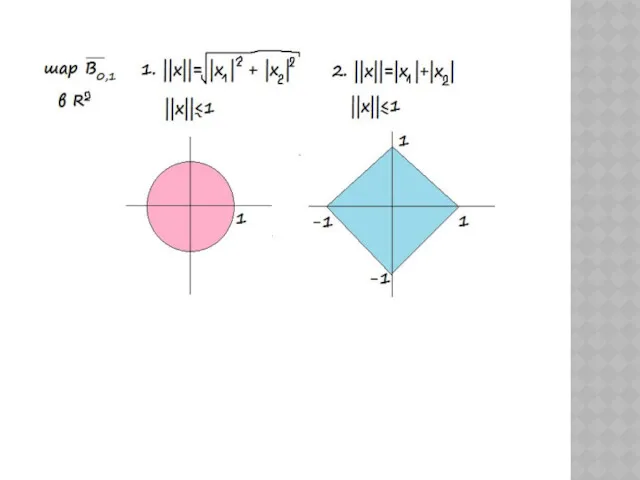
- 23. ПРИМЕРЫ ШАРОВ
- 25. ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ Пусть X,Y-н.п.А: Х→Y – линейный оператор Определение. Оператор А называется ограниченным, если он
- 26. ПРИМЕРЫ НЕПРЕРЫВНЫХ ОПЕРАТОРОВ
- 27. КРИТЕРИЙ НЕПРЕРЫВНОСТИ Пусть A: → - л.о., тогда (A непрерывен)⇔(A непрерывен в т. θ)⇔ (А ограничен)⇔
- 28. 2°⇒3°⇒4°⇒2°? 2°⇒3°? Предположим противное: [ X⊃D - ограниченное, но A(D) не ограничено] =(определение ограниченного множества)⇒ A(D)
- 29. 3°⇒4°? Предположим противное: не 4°, т.е. ∀n∈N ∃ xn ≠ θ (?) | ||Axn||Y > n||xn||
- 30. 4°⇒2°? xn → θX ⇐(определение сходящейся послед -ти)⇒ ||xn||X → 0 =(||Ax||Y ≤ М||x||X)⇒ 0 ≤
- 31. НОРМА Л.Н.О. A:X→Y- л.н.о. Для линейных операторов непрерывность эквивалентна его ограниченности Оператор А – ограничен Наименьшей
- 32. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ НОРМЫ А Теорема Формулы для вычисления нормы л.н.о. A∈N(X,Y): ||A|| = (α) sup{⎟⎢Ax⎟⎢Y:⎟⎢x⎟⎢X
- 33. ВЫЧИСЛЕНИЕ НОРМЫ ОПЕРАТОРА
- 35. ВЫЧИСЛЕНИЕ НОРМЫ ОПЕРАТОРА
- 36. ВЫЧИСЛЕНИЕ НОРМЫ ОПЕРАТОРА
- 37. СВОЙСТВА Л.Н.О. Множество всех л.н.о. , действующих из Х в Y, обозначим N(X,Y). 1)N(X,Y) нормированное пространство
- 38. СВОЙСТВА К/М Н.П. Теорема. В конечномерном н.п. 1) ∀ две нормы эквивалентны; 2) сходимость по любой
- 39. ТЕОРЕМЫ ОБ ОПЕРАТОРАХ В Б.П. Теорема о продолжении по непрерывности. (Х - н.п., Y - б.п.,
- 40. Теорема об открытом отображении. Пусть A∈ N(X - б.п., Y - б.п.); тогда (А - открытое
- 41. Следствия. Об эквивалентности норм. ( - б.п., - б.п. & ∃ c>0⏐|| . ||α ≤ c||
- 43. Скачать презентацию

![ПРИМЕРЫ НОРМ 1.X=B[a, b] ( X=C[a, b]) 2. X=L1[a, b] 3. X=L2[a, b] 4. X=l1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/132211/slide-2.jpg)


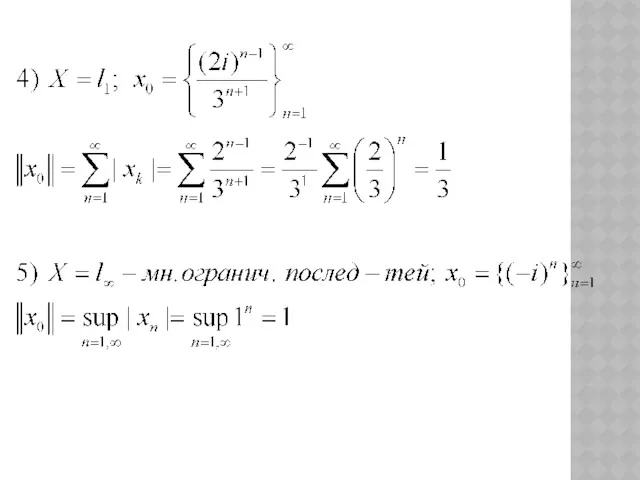

























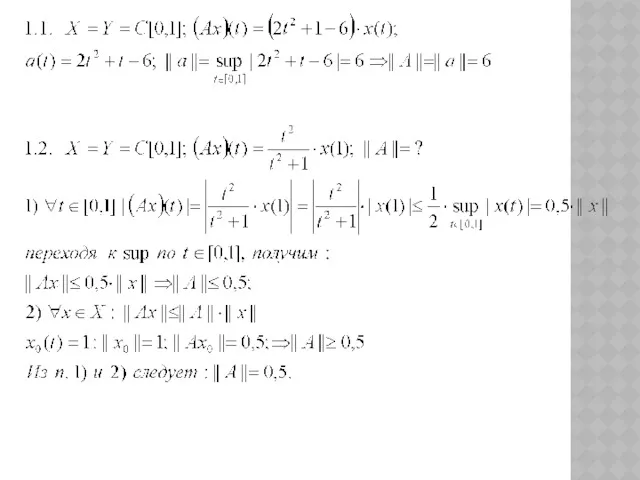







 Тірек векторлар көмегімен классификациялау
Тірек векторлар көмегімен классификациялау Игра для проведения устного счета в 1 классе
Игра для проведения устного счета в 1 классе Методы поиска условного экстремума
Методы поиска условного экстремума Разложение вектора по трем некомпланарным векторам
Разложение вектора по трем некомпланарным векторам Делим на части
Делим на части Конспект совместной деятельности с детьми младшего дошкольного возраста
Конспект совместной деятельности с детьми младшего дошкольного возраста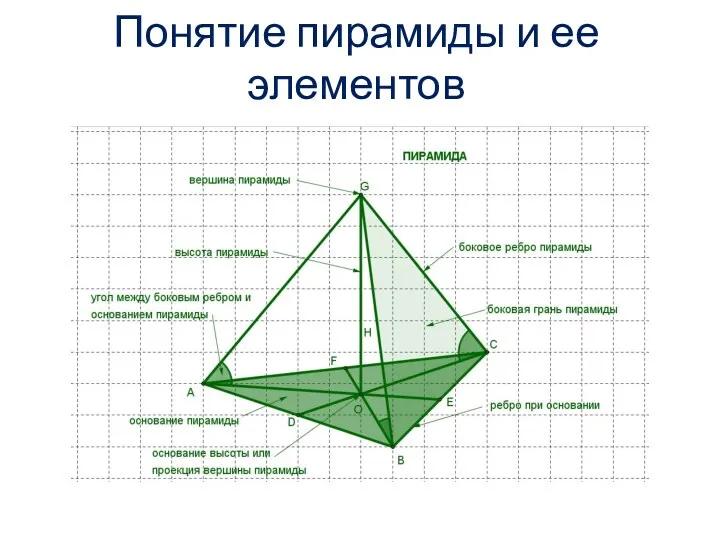 Понятие пирамиды и ее элементов. Правильная пирамида
Понятие пирамиды и ее элементов. Правильная пирамида Параллель, қиылысатын және айқас түзулер
Параллель, қиылысатын және айқас түзулер Решение рациональных неравенств
Решение рациональных неравенств Решение задач части В
Решение задач части В Тригонометрические уравнения
Тригонометрические уравнения Тренажер по таблице умножения и деления
Тренажер по таблице умножения и деления Первый признак подобия треугольников
Первый признак подобия треугольников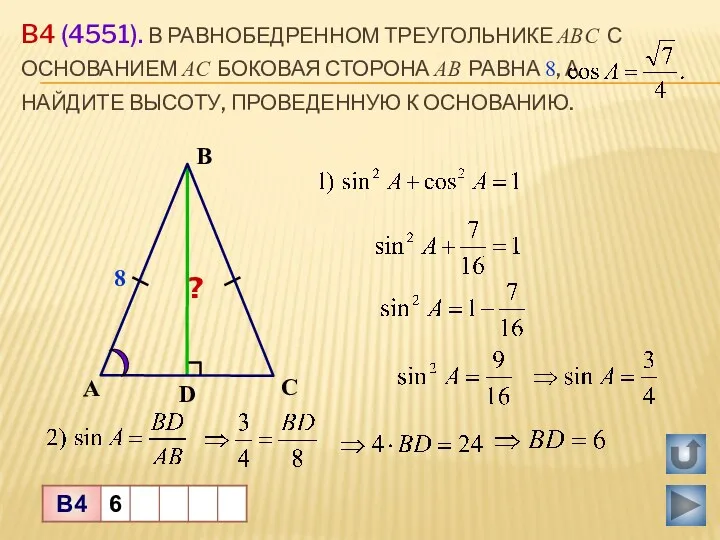 Знаки тригонометрических функций
Знаки тригонометрических функций Численное решение уравнений нелинейной оптики
Численное решение уравнений нелинейной оптики Випадкові величини
Випадкові величини Розкладання квадратного тричлена на множники
Розкладання квадратного тричлена на множники Треугольники. Основные признаки и свойства треугольников
Треугольники. Основные признаки и свойства треугольников Комбинаторика. Правило суммы и правило произведения
Комбинаторика. Правило суммы и правило произведения Интерактивная математическая раскраска
Интерактивная математическая раскраска Таблица умножения на 2,3,4,5 и второй на 6,7,8,9
Таблица умножения на 2,3,4,5 и второй на 6,7,8,9 Нахождение неизвестного слагаемого в усложненном уравнении
Нахождение неизвестного слагаемого в усложненном уравнении Математика о вреде курения. 6 класс
Математика о вреде курения. 6 класс Методика изучения арифметических действий
Методика изучения арифметических действий Взаимное пересечение кривых поверхностей. Лекция 12
Взаимное пересечение кривых поверхностей. Лекция 12 Повторение знаний о нумерации. Числа от 11 до 20
Повторение знаний о нумерации. Числа от 11 до 20 Извлечение квадратных корней из больших чисел без калькулятора
Извлечение квадратных корней из больших чисел без калькулятора Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей